In-context learning (ICL), a key feature of modern large language models (LLMs), allows transformers to adapt based on examples within the input prompt. Few-shot prompting, using several task examples, effectively demonstrates the desired behavior. But how do transformers achieve this adaptation? This article explores potential mechanisms behind ICL.

The core of ICL is: given example pairs ((x,y)), can attention mechanisms learn an algorithm to map new queries (x) to their outputs (y)?
Softmax Attention and Nearest Neighbor Search
The softmax attention formula is:

Introducing an inverse temperature parameter, c, modifies the attention allocation:

As c approaches infinity, attention becomes a one-hot vector, focusing solely on the most similar token – effectively a nearest neighbor search. With finite c, attention resembles Gaussian kernel smoothing. This suggests ICL might implement a nearest neighbor algorithm on input-output pairs.
Implications and Further Research
Understanding how transformers learn algorithms (like nearest neighbor) opens doors for AutoML. Hollmann et al. demonstrated training a transformer on synthetic datasets to learn the entire AutoML pipeline, predicting optimal models and hyperparameters from new data in a single pass.
Anthropic's 2022 research suggests "induction heads" as a mechanism. These pairs of attention heads copy and complete patterns; for example, given "...A, B...A", they predict "B" based on prior context.
Recent studies (Garg et al. 2022, Oswald et al. 2023) link transformers' ICL to gradient descent. Linear attention, omitting the softmax operation:

Resembles preconditioned gradient descent (PGD):

One layer of linear attention performs one PGD step.
Conclusion
Attention mechanisms can implement learning algorithms, enabling ICL by learning from demonstration pairs. While the interplay of multiple attention layers and MLPs is complex, research sheds light on ICL's mechanics. This article offers a high-level overview of these insights.
Further Reading:
- In-context Learning and Induction Heads
- What Can Transformers Learn In-Context? A Case Study of Simple Function Classes
- Transformers Learn In-Context by Gradient Descent
- Transformers learn to implement preconditioned gradient descent for in-context learning
Acknowledgment
This article is inspired by Fall 2024 graduate coursework at the University of Michigan. Any errors are solely the author's.
The above is the detailed content of The Math Behind In-Context Learning. For more information, please follow other related articles on the PHP Chinese website!
 What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AM
What is Graph of Thought in Prompt EngineeringApr 13, 2025 am 11:53 AMIntroduction In prompt engineering, “Graph of Thought” refers to a novel approach that uses graph theory to structure and guide AI’s reasoning process. Unlike traditional methods, which often involve linear s
 Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AM
Optimize Your Organisation's Email Marketing with GenAI AgentsApr 13, 2025 am 11:44 AMIntroduction Congratulations! You run a successful business. Through your web pages, social media campaigns, webinars, conferences, free resources, and other sources, you collect 5000 email IDs daily. The next obvious step is
 Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AM
Real-Time App Performance Monitoring with Apache PinotApr 13, 2025 am 11:40 AMIntroduction In today’s fast-paced software development environment, ensuring optimal application performance is crucial. Monitoring real-time metrics such as response times, error rates, and resource utilization can help main
 ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM
ChatGPT Hits 1 Billion Users? 'Doubled In Just Weeks' Says OpenAI CEOApr 13, 2025 am 11:23 AM“How many users do you have?” he prodded. “I think the last time we said was 500 million weekly actives, and it is growing very rapidly,” replied Altman. “You told me that it like doubled in just a few weeks,” Anderson continued. “I said that priv
 Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AM
Pixtral-12B: Mistral AI's First Multimodal Model - Analytics VidhyaApr 13, 2025 am 11:20 AMIntroduction Mistral has released its very first multimodal model, namely the Pixtral-12B-2409. This model is built upon Mistral’s 12 Billion parameter, Nemo 12B. What sets this model apart? It can now take both images and tex
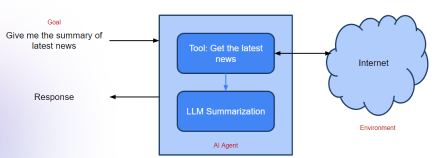 Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AM
Agentic Frameworks for Generative AI Applications - Analytics VidhyaApr 13, 2025 am 11:13 AMImagine having an AI-powered assistant that not only responds to your queries but also autonomously gathers information, executes tasks, and even handles multiple types of data—text, images, and code. Sounds futuristic? In this a
 Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AM
Applications of Generative AI in the Financial SectorApr 13, 2025 am 11:12 AMIntroduction The finance industry is the cornerstone of any country’s development, as it drives economic growth by facilitating efficient transactions and credit availability. The ease with which transactions occur and credit
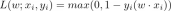 Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AM
Guide to Online Learning and Passive-Aggressive AlgorithmsApr 13, 2025 am 11:09 AMIntroduction Data is being generated at an unprecedented rate from sources such as social media, financial transactions, and e-commerce platforms. Handling this continuous stream of information is a challenge, but it offers an


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

SublimeText3 Chinese version
Chinese version, very easy to use

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

Dreamweaver Mac version
Visual web development tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.






