Key Takeaways
- Graphs are mathematical constructs used to model relationships between key/value pairs and have numerous real-world applications such as network optimization, traffic routing, and social network analysis. They are made up of vertices (nodes) and edges (lines) that connect them, which can be directed or undirected, and weighted or unweighted.
- Graphs can be represented in two ways: as an adjacency matrix or an adjacency list. Adjacency lists are more space-efficient, especially for sparse graphs where most pairs of vertices are unconnected, while adjacency matrices facilitate quicker lookups.
- A common application of graph theory is finding the least number of hops (i.e., the shortest path) between any two nodes. This can be achieved using breadth-first search, which involves traversing the graph level by level from a designated root node. This process requires maintaining a queue of unvisited nodes.
- Dijkstra’s algorithm is widely used to find the shortest or most optimal path between any two nodes in a graph. This involves examining each edge between all possible pairs of vertices, starting from the source node, and maintaining an updated set of vertices with the shortest total distance until the target node is reached.
The Least Number of Hops
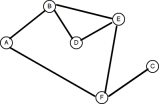
A common application of graph theory is finding the least number of hops between any two nodes. As with trees, graphs can be traversed in one of two ways: depth-first or breadth-first. We covered depth-first search in the previous article, so let’s take a look at breadth-first search. Consider the following graph:
1. Create a queue 2. Enqueue the root node and mark it as visited 3. While the queue is not empty do: 3a. dequeue the current node 3b. if the current node is the one we're looking for then stop 3c. else enqueue each unvisited adjacent node and mark as visitedBut how do we know which nodes are adjacent, let alone unvisited, without traversing the graph first? This brings us to the problem of how a graph data structure can be modelled.
Representing the Graph
There are generally two ways to represent a graph: either as an adjacency matrix or an adjacency list. The above graph represented as an adjacency list looks like this:

1. Create a queue 2. Enqueue the root node and mark it as visited 3. While the queue is not empty do: 3a. dequeue the current node 3b. if the current node is the one we're looking for then stop 3c. else enqueue each unvisited adjacent node and mark as visitedAnd now, let’s see what the general breadth-first search algorithm’s implementation looks like:
<span><span><?php </span></span><span><span>$graph = array(
</span></span><span> <span>'A' => array('B', 'F'),
</span></span><span> <span>'B' => array('A', 'D', 'E'),
</span></span><span> <span>'C' => array('F'),
</span></span><span> <span>'D' => array('B', 'E'),
</span></span><span> <span>'E' => array('B', 'D', 'F'),
</span></span><span> <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>
Running the following examples, we get:
<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span> <span>protected $graph;
</span></span><span> <span>protected $visited = array();
</span></span><span>
</span><span> <span>public function __construct($graph) {
</span></span><span> <span>$this->graph = $graph;
</span></span><span> <span>}
</span></span><span>
</span><span> <span>// find least number of hops (edges) between 2 nodes
</span></span><span> <span>// (vertices)
</span></span><span> <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span> <span>// mark all nodes as unvisited
</span></span><span> <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span> <span>$this->visited[$vertex] = false;
</span></span><span> <span>}
</span></span><span>
</span><span> <span>// create an empty queue
</span></span><span> <span>$q = new SplQueue();
</span></span><span>
</span><span> <span>// enqueue the origin vertex and mark as visited
</span></span><span> <span>$q->enqueue($origin);
</span></span><span> <span>$this->visited[$origin] = true;
</span></span><span>
</span><span> <span>// this is used to track the path back from each node
</span></span><span> <span>$path = array();
</span></span><span> <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span> <span>$path[$origin]->setIteratorMode(
</span></span><span> <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span> <span>);
</span></span><span>
</span><span> <span>$path[$origin]->push($origin);
</span></span><span>
</span><span> <span>$found = false;
</span></span><span> <span>// while queue is not empty and destination not found
</span></span><span> <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span> <span>$t = $q->dequeue();
</span></span><span>
</span><span> <span>if (!empty($this->graph[$t])) {
</span></span><span> <span>// for each adjacent neighbor
</span></span><span> <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span> <span>if (!$this->visited[$vertex]) {
</span></span><span> <span>// if not yet visited, enqueue vertex and mark
</span></span><span> <span>// as visited
</span></span><span> <span>$q->enqueue($vertex);
</span></span><span> <span>$this->visited[$vertex] = true;
</span></span><span> <span>// add vertex to current path
</span></span><span> <span>$path[$vertex] = clone $path[$t];
</span></span><span> <span>$path[$vertex]->push($vertex);
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span>
</span><span> <span>if (isset($path[$destination])) {
</span></span><span> <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>,
</span></span><span> <span>count($path[$destination]) - 1,
</span></span><span> <span>" hopsn";
</span></span><span> <span>$sep = '';
</span></span><span> <span>foreach ($path[$destination] as $vertex) {
</span></span><span> <span>echo $sep, $vertex;
</span></span><span> <span>$sep = '->';
</span></span><span> <span>}
</span></span><span> <span>echo "n";
</span></span><span> <span>}
</span></span><span> <span>else {
</span></span><span> <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span><span>}</span></span></span>
If we had used a stack instead of a queue, the traversal becomes a depth-first search.
Finding the Shortest-Path
Another common problem is finding the most optimal path between any two nodes. Earlier I mentioned GoogleMap’s driving directions as an example of this. Other applications include planning travel itineraries, road traffic management, and train/bus scheduling. One of the most famous algorithms to address this problem was invented in 1959 by a 29 year-old computer scientist by the name of Edsger W. Dijkstra. In general terms, Dijkstra’s solution involves examining each edge between all possible pairs of vertices starting from the source node and maintaining an updated set of vertices with the shortest total distance until the target node is reached, or not reached, whichever the case may be. There are several ways to implement the solution, and indeed, over years following 1959 many enhancements – using MinHeaps, PriorityQueues, and Fibonacci Heaps – were made to Dijkstra’s original algorithm. Some improved performance, while others were designed to address shortcomings in Dijkstra’s solution since it only worked with positive weighted graphs (where the weights are positive values). Here’s an example of a (positive) weighted graph: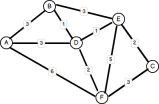
1. Create a queue 2. Enqueue the root node and mark it as visited 3. While the queue is not empty do: 3a. dequeue the current node 3b. if the current node is the one we're looking for then stop 3c. else enqueue each unvisited adjacent node and mark as visitedAnd here’s an implementation using a PriorityQueue to maintain a list of all “unoptimized” vertices:
<span><span><?php </span></span><span><span>$graph = array(
</span></span><span> <span>'A' => array('B', 'F'),
</span></span><span> <span>'B' => array('A', 'D', 'E'),
</span></span><span> <span>'C' => array('F'),
</span></span><span> <span>'D' => array('B', 'E'),
</span></span><span> <span>'E' => array('B', 'D', 'F'),
</span></span><span> <span>'F' => array('A', 'E', 'C'),
</span></span><span><span>);</span></span></span>
As you can see, Dijkstra’s solution is simply a variation of the breadth-first search!
Running the following examples yields the following results:
<span><span><?php </span></span><span><span>class Graph
</span></span><span><span>{
</span></span><span> <span>protected $graph;
</span></span><span> <span>protected $visited = array();
</span></span><span>
</span><span> <span>public function __construct($graph) {
</span></span><span> <span>$this->graph = $graph;
</span></span><span> <span>}
</span></span><span>
</span><span> <span>// find least number of hops (edges) between 2 nodes
</span></span><span> <span>// (vertices)
</span></span><span> <span>public function breadthFirstSearch($origin, $destination) {
</span></span><span> <span>// mark all nodes as unvisited
</span></span><span> <span>foreach ($this->graph as $vertex => $adj) {
</span></span><span> <span>$this->visited[$vertex] = false;
</span></span><span> <span>}
</span></span><span>
</span><span> <span>// create an empty queue
</span></span><span> <span>$q = new SplQueue();
</span></span><span>
</span><span> <span>// enqueue the origin vertex and mark as visited
</span></span><span> <span>$q->enqueue($origin);
</span></span><span> <span>$this->visited[$origin] = true;
</span></span><span>
</span><span> <span>// this is used to track the path back from each node
</span></span><span> <span>$path = array();
</span></span><span> <span>$path[$origin] = new SplDoublyLinkedList();
</span></span><span> <span>$path[$origin]->setIteratorMode(
</span></span><span> <span>SplDoublyLinkedList<span>::</span>IT_MODE_FIFO|SplDoublyLinkedList<span>::</span>IT_MODE_KEEP
</span></span><span> <span>);
</span></span><span>
</span><span> <span>$path[$origin]->push($origin);
</span></span><span>
</span><span> <span>$found = false;
</span></span><span> <span>// while queue is not empty and destination not found
</span></span><span> <span>while (!$q->isEmpty() && $q->bottom() != $destination) {
</span></span><span> <span>$t = $q->dequeue();
</span></span><span>
</span><span> <span>if (!empty($this->graph[$t])) {
</span></span><span> <span>// for each adjacent neighbor
</span></span><span> <span>foreach ($this->graph[$t] as $vertex) {
</span></span><span> <span>if (!$this->visited[$vertex]) {
</span></span><span> <span>// if not yet visited, enqueue vertex and mark
</span></span><span> <span>// as visited
</span></span><span> <span>$q->enqueue($vertex);
</span></span><span> <span>$this->visited[$vertex] = true;
</span></span><span> <span>// add vertex to current path
</span></span><span> <span>$path[$vertex] = clone $path[$t];
</span></span><span> <span>$path[$vertex]->push($vertex);
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span>
</span><span> <span>if (isset($path[$destination])) {
</span></span><span> <span>echo "<span><span>$origin</span> to <span>$destination</span> in "</span>,
</span></span><span> <span>count($path[$destination]) - 1,
</span></span><span> <span>" hopsn";
</span></span><span> <span>$sep = '';
</span></span><span> <span>foreach ($path[$destination] as $vertex) {
</span></span><span> <span>echo $sep, $vertex;
</span></span><span> <span>$sep = '->';
</span></span><span> <span>}
</span></span><span> <span>echo "n";
</span></span><span> <span>}
</span></span><span> <span>else {
</span></span><span> <span>echo "No route from <span><span>$origin</span> to <span>$destinationn</span>"</span>;
</span></span><span> <span>}
</span></span><span> <span>}
</span></span><span><span>}</span></span></span>
Summary
In this article I’ve introduced the basics of graph theory, two ways of representing graphs, and two fundamental problems in the application of graph theory. I’ve shown you how a breadth-first search is used to find the least number of hops between any two nodes, and how Dijkstra’s solution is used to find the shortest-path between any two nodes. Image via FotoliaFrequently Asked Questions (FAQs) about Graphs in Data Structures
What is the difference between a graph and a tree in data structures?
A graph and a tree are both non-linear data structures, but they have some key differences. A tree is a type of graph, but not all graphs are trees. A tree is a connected graph without any cycles. It has a hierarchical structure with a root node and child nodes. Each node in a tree has a unique path from the root. On the other hand, a graph can have cycles and its structure is more complex. It can be connected or disconnected and nodes can have multiple paths between them.
How are graphs represented in data structures?
Graphs in data structures can be represented in two ways: adjacency matrix and adjacency list. An adjacency matrix is a 2D array of size V x V where V is the number of vertices in the graph. If there is an edge between vertices i and j, then the cell at the intersection of row i and column j will be 1, otherwise 0. An adjacency list is an array of linked lists. The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.
What are the types of graphs in data structures?
There are several types of graphs in data structures. A simple graph is a graph with no loops and no more than one edge between any two vertices. A multigraph can have multiple edges between vertices. A complete graph is a simple graph where every pair of vertices is connected by an edge. A weighted graph assigns a weight to each edge. A directed graph (or digraph) has edges with a direction. The edges point from one vertex to another.
What are the applications of graphs in computer science?
Graphs are used in numerous applications in computer science. They are used in social networks to represent connections between people. They are used in web crawling to visit web pages and build a search index. They are used in network routing algorithms to find the best path between two nodes. They are used in biology to model and analyze biological networks. They are also used in computer graphics and physics simulations.
What are the graph traversal algorithms?
There are two main graph traversal algorithms: Depth-First Search (DFS) and Breadth-First Search (BFS). DFS explores as far as possible along each branch before backtracking. It uses a stack data structure. BFS explores all the vertices at the present depth before going to the next level. It uses a queue data structure.
How to implement a graph in Java?
In Java, a graph can be implemented using a HashMap to store the adjacency list. Each key in the HashMap is a vertex and its value is a LinkedList containing the vertices that it is connected to.
What is a bipartite graph?
A bipartite graph is a graph whose vertices can be divided into two disjoint sets such that every edge connects a vertex in one set to a vertex in the other set. No edge connects vertices within the same set.
What is a subgraph?
A subgraph is a graph that is a part of another graph. It has some (or all) vertices of the original graph and some (or all) edges of the original graph.
What is a cycle in a graph?
A cycle in a graph is a path that starts and ends at the same vertex and has at least one edge.
What is a path in a graph?
A path in a graph is a sequence of vertices where each pair of consecutive vertices is connected by an edge.
The above is the detailed content of PHP Master | Data Structures for PHP Devs: Graphs. For more information, please follow other related articles on the PHP Chinese website!
 11 Best PHP URL Shortener Scripts (Free and Premium)Mar 03, 2025 am 10:49 AM
11 Best PHP URL Shortener Scripts (Free and Premium)Mar 03, 2025 am 10:49 AMLong URLs, often cluttered with keywords and tracking parameters, can deter visitors. A URL shortening script offers a solution, creating concise links ideal for social media and other platforms. These scripts are valuable for individual websites a
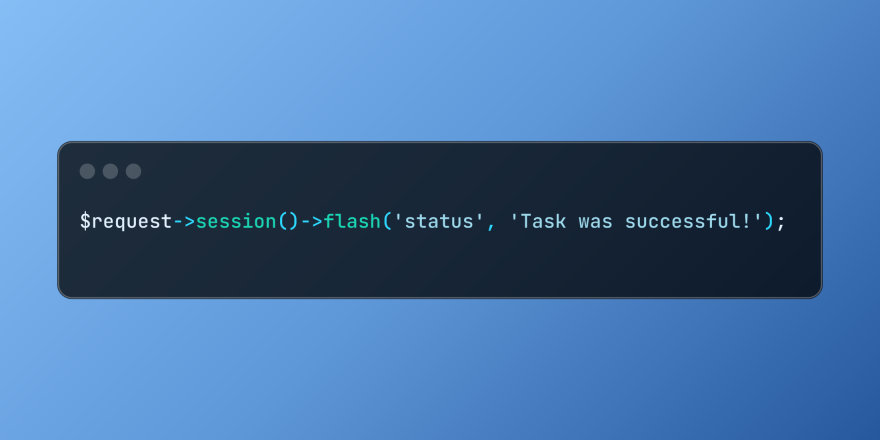 Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PM
Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PMLaravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 Build a React App With a Laravel Back End: Part 2, ReactMar 04, 2025 am 09:33 AM
Build a React App With a Laravel Back End: Part 2, ReactMar 04, 2025 am 09:33 AMThis is the second and final part of the series on building a React application with a Laravel back-end. In the first part of the series, we created a RESTful API using Laravel for a basic product-listing application. In this tutorial, we will be dev
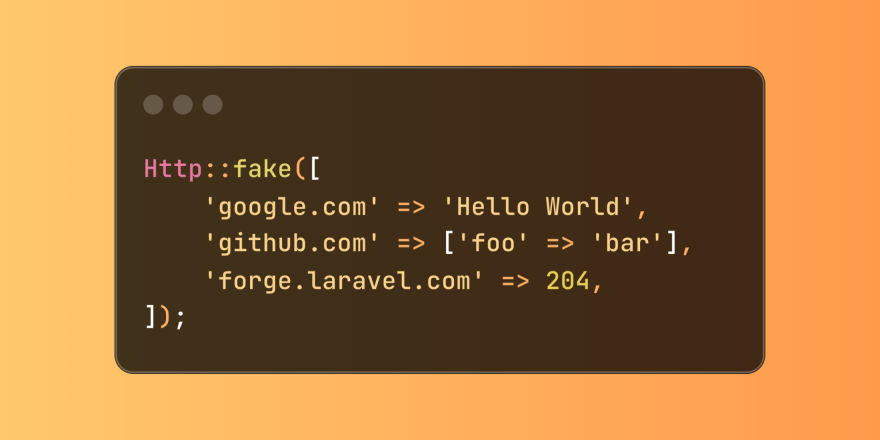 Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PMLaravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AMThe PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
 12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PMDo you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 Announcement of 2025 PHP Situation SurveyMar 03, 2025 pm 04:20 PM
Announcement of 2025 PHP Situation SurveyMar 03, 2025 pm 04:20 PMThe 2025 PHP Landscape Survey investigates current PHP development trends. It explores framework usage, deployment methods, and challenges, aiming to provide insights for developers and businesses. The survey anticipates growth in modern PHP versio
 Notifications in LaravelMar 04, 2025 am 09:22 AM
Notifications in LaravelMar 04, 2025 am 09:22 AMIn this article, we're going to explore the notification system in the Laravel web framework. The notification system in Laravel allows you to send notifications to users over different channels. Today, we'll discuss how you can send notifications ov


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Zend Studio 13.0.1
Powerful PHP integrated development environment

Atom editor mac version download
The most popular open source editor

ZendStudio 13.5.1 Mac
Powerful PHP integrated development environment

SublimeText3 Mac version
God-level code editing software (SublimeText3)

Dreamweaver Mac version
Visual web development tools







