Understanding Quick Sort Algorithm (with Examples in Java)

Detailed explanation of QuickSort algorithm: an efficient sorting tool

QuickSort is an efficient sorting algorithm based on the divide-and-conquer strategy. The divide-and-conquer method decomposes the problem into smaller sub-problems, solves these sub-problems separately, and then combines the solutions of the sub-problems to obtain the final solution. In quick sort, an array is divided by selecting a partition element, which determines the split point of the array. Before partitioning, the position of the partitioning element is rearranged so that it is before the element that is larger than it and after the element that is smaller than it. The left and right subarrays will be divided recursively in this manner until each subarray contains only one element, at which point the array is sorted.

How quick sort works

Let us sort the following array in ascending order as an example:

Step 1: Select the pivot element

We choose the last element as the pivot:

Step 2: Rearrange pivot elements

We place the pivot element before elements that are larger than it and after elements that are smaller than it. To do this, we will iterate through the array and compare the pivot to each element before it. If an element larger than the pivot is found, we create a second pointer for it:

If an element smaller than the pivot is found, we swap it with the second pointer:

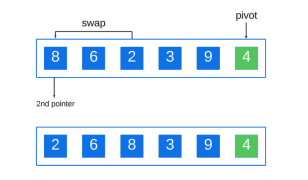
Repeat this process, setting the next element larger than the pivot to the second pointer, swapping if an element smaller than the pivot is found:

Continue this process until you reach the end of the array:

After completing the element comparison, the element smaller than the pivot has been moved to the right, then we swap the pivot with the second pointer:

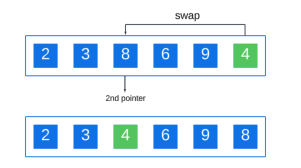
Step 3: Divide the array

Divide the array according to the partition index. If we represent the array as arr[start..end], then by dividing the array by partition, we can get the left subarray arr[start..partitionIndex-1] and the right subarray arr[partitionIndex 1..end].

Continue dividing the subarrays in this way until each subarray contains only one element:

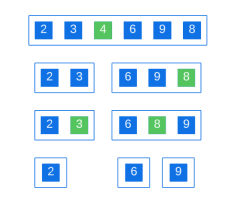
At this point, the array is sorted.

Quick sort code implementation

import java.util.Arrays;

public class QuickSortTest {
    public static void main(String[] args){
        int[] arr = {8, 6, 2, 3, 9, 4};
        System.out.println("未排序数组: " + Arrays.toString(arr));
        quickSort(arr, 0, arr.length-1);
        System.out.println("已排序数组: " + Arrays.toString(arr));
    }

    public static int partition(int[] arr, int start, int end){
        // 将最后一个元素设置为枢轴
        int pivot = arr[end];
        // 创建指向下一个较大元素的指针
        int secondPointer = start-1;

        // 将小于枢轴的元素移动到枢轴左侧
        for (int i = start; i < end; i++){
            if (arr[i] < pivot){
                secondPointer++;
                // 交换元素
                int temp = arr[secondPointer];
                arr[secondPointer] = arr[i];
                arr[i] = temp;
            }
        }
        // 将枢轴与第二个指针交换
        int temp = arr[secondPointer+1];
        arr[secondPointer+1] = arr[end];
        arr[end] = temp;
        // 返回分区索引
        return secondPointer+1;
    }

    public static void quickSort(int[] arr, int start, int end){
        if (start < end){
            // 找到分区索引
            int partitionIndex = partition(arr, start, end);
            // 递归调用快速排序
            quickSort(arr, start, partitionIndex-1);
            quickSort(arr, partitionIndex+1, end);
        }
    }
}

Code interpretation

quickSort method: First call the partition method to divide the array into two sub-arrays, and then call quickSort recursively to sort the left and right sub-arrays. This process continues until all subarrays contain exactly one element, at which point the array is sorted.

partition Method: Responsible for dividing the array into two sub-arrays. It first sets the pivot and the pointer to the next larger element, then iterates through the array, moving elements smaller than the pivot to the left. After that it swaps the pivot with the second pointer and returns the partition position.

Run the above code, the console will output the following:

Unsorted array: [8, 6, 2, 3, 9, 4] Sorted array: [2, 3, 4, 6, 8, 9]

Time complexity

Best case (O(n log n)): The best case occurs when the pivot splits the array into two nearly equal parts every time.

Average case (O(n log n)): In the average case, the pivot splits the array into two unequal parts, but the recursion depth and number of comparisons are still proportional to n log n.

Worst case (O(n²)): The worst case occurs when the pivot always splits the array into very unequal parts (e.g. one part has only one element and the other has n-1 elements) . This can happen, for example, when sorting an array in reverse order, and the pivot is chosen poorly.

Space complexity (O(log n)): Quick sort is usually implemented in-place and does not require additional arrays.

The above is the detailed content of Understanding Quick Sort Algorithm (with Examples in Java). For more information, please follow other related articles on the PHP Chinese website!