 Backend Development
Backend Development PHP Tutorial
PHP Tutorial How Many Permutations Exist for a Set of Nine Numbers and How Can They Be Generated in PHP?
How Many Permutations Exist for a Set of Nine Numbers and How Can They Be Generated in PHP?
Enumerating all Permutation Sets of Numbers
In the realm of combinatorics, a permutation refers to an ordered arrangement of elements from a given set. Given a set of numbers ranging from 0 to 8, the challenge is to generate all possible permutations where each number appears exactly once in a set.
Calculating Permutations
The formula for calculating the number of permutations of n elements, taken k at a time, is:
nPk = n! / (n - k)!
In this case, where n = 9 and k = 9, we have:
9P9 = 9! = 362,880
Therefore, there are 362,880 possible permutations of the given set.
PHP Implementation
One way to generate these permutations in PHP is through a recursive algorithm:
<?php pc_permute([0, 1, 2, 3, 4, 5, 7, 8]);
function pc_permute($items, $perms = array()) {
if (empty($items)) {
print join(' ', $perms) . "\n";
} else {
for ($i = count($items) - 1; $i >= 0; --$i) {
$newitems = $items;
$newperms = $perms;
list($foo) = array_splice($newitems, $i, 1);
array_unshift($newperms, $foo);
pc_permute($newitems, $newperms);
}
}
}
?>
Sample Output
Running this code will produce the following sample permutations:
0 1 2 3 4 5 6 7 8 0 1 2 3 4 5 6 8 7 0 1 2 3 4 5 7 6 8 0 1 2 3 4 5 7 8 6 0 1 2 3 4 5 8 6 7 0 1 2 3 4 5 8 7 6 ...
The above is the detailed content of How Many Permutations Exist for a Set of Nine Numbers and How Can They Be Generated in PHP?. For more information, please follow other related articles on the PHP Chinese website!
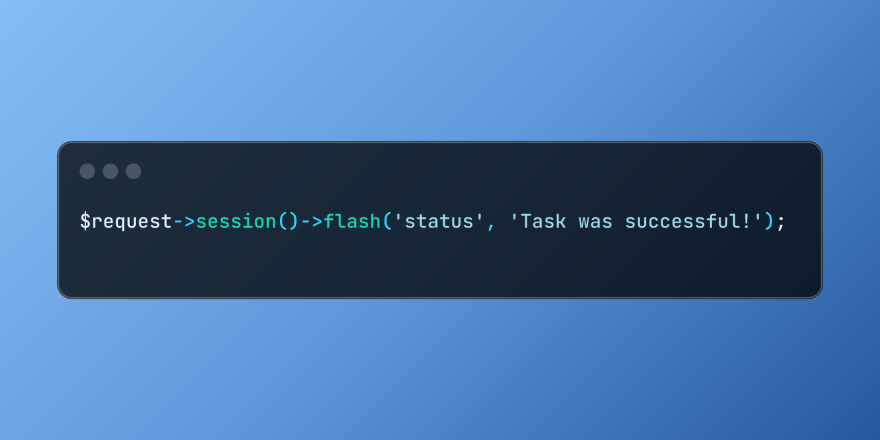 Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PM
Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PMLaravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AMThe PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
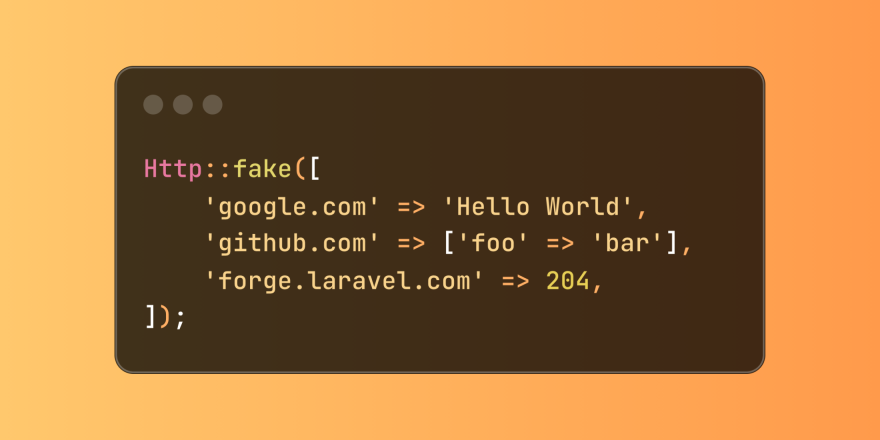 Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PMLaravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PMDo you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 How to Register and Use Laravel Service ProvidersMar 07, 2025 am 01:18 AM
How to Register and Use Laravel Service ProvidersMar 07, 2025 am 01:18 AMLaravel's service container and service providers are fundamental to its architecture. This article explores service containers, details service provider creation, registration, and demonstrates practical usage with examples. We'll begin with an ove
 Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PM
Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PMArticle discusses late static binding (LSB) in PHP, introduced in PHP 5.3, allowing runtime resolution of static method calls for more flexible inheritance.Main issue: LSB vs. traditional polymorphism; LSB's practical applications and potential perfo
 PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PM
PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PMPHP logging is essential for monitoring and debugging web applications, as well as capturing critical events, errors, and runtime behavior. It provides valuable insights into system performance, helps identify issues, and supports faster troubleshoot
 Customizing/Extending Frameworks: How to add custom functionality.Mar 28, 2025 pm 05:12 PM
Customizing/Extending Frameworks: How to add custom functionality.Mar 28, 2025 pm 05:12 PMThe article discusses adding custom functionality to frameworks, focusing on understanding architecture, identifying extension points, and best practices for integration and debugging.


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

MinGW - Minimalist GNU for Windows
This project is in the process of being migrated to osdn.net/projects/mingw, you can continue to follow us there. MinGW: A native Windows port of the GNU Compiler Collection (GCC), freely distributable import libraries and header files for building native Windows applications; includes extensions to the MSVC runtime to support C99 functionality. All MinGW software can run on 64-bit Windows platforms.

SublimeText3 Chinese version
Chinese version, very easy to use

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

SublimeText3 Linux new version
SublimeText3 Linux latest version




