 Web Front-end
Web Front-end JS Tutorial
JS Tutorial Understanding and Implementing the Karatsuba Multiplication Algorithm for Large Numbers
Understanding and Implementing the Karatsuba Multiplication Algorithm for Large Numbers
In computational mathematics, efficiently multiplying large numbers is a cornerstone of various applications, from cryptography to scientific computing. The Karatsuba multiplication algorithm is a divide-and-conquer method that significantly improves performance over traditional long multiplication for large numbers. In this article, we'll explore a JavaScript implementation of this powerful algorithm designed to handle arbitrarily large numbers represented as strings.
The Problem with Traditional Multiplication
The standard "schoolbook" multiplication method has a time complexity of (O(n2)) , where (n) is the number of digits in the numbers being multiplied. This quadratic growth becomes computationally expensive as the numbers grow larger. The Karatsuba algorithm, introduced by Anatolii Karatsuba in 1960, reduces this complexity to approximately (O(n1.585)) , making it a much faster option for large inputs.
How the Karatsuba Algorithm Works
The algorithm relies on the divide-and-conquer strategy:
- Divide: Split each number into two halves—a high part and a low part.
-
Conquer: Compute three key products recursively: This involves calculating the following components for each recursive step:
- z0=low1×low2
- z1=(low1 high1)×(low2 high2)
- z2=high1×high2
-
Combine: Use the formula:
result=z2⋅102⋅m (z1−z2−z0)⋅10m z0where (m) is half the number of digits in the original numbers.
This approach reduces the number of recursive multiplications from four to three, improving efficiency.
JavaScript Implementation
Below is a robust implementation of the Karatsuba algorithm in JavaScript. This version supports arbitrarily large integers by representing them as strings.
multiply.js
/**
* Karatsuba multiplication algorithm for large numbers.
* @param {string} num1 - First large number as a string.
* @param {string} num2 - Second large number as a string.
* @returns {string} - Product of the two numbers as a string.
*/
function karatsubaMultiply(num1, num2) {
// Remove leading zeros
num1 = num1.replace(/^0+/, "") || "0";
num2 = num2.replace(/^0+/, "") || "0";
// If either number is zero, return "0"
if (num1 === "0" || num2 === "0") return "0";
// Base case for small numbers (12), use Number for safe multiplication
if (num1.length = 0; i--) {
const sum = parseInt(a[i]) + parseInt(b[i]) + carry;
result = (sum % 10) + result;
carry = Math.floor(sum / 10);
}
if (carry > 0) {
result = carry + result;
}
return result.replace(/^0+/, "") || "0";
}
// Helper function to multiply by 10^n
function multiplyByPowerOf10(num, power) {
return num === "0" ? "0" : num + "0".repeat(power);
}
// Helper function for subtracting large numbers
function subtractLargeNumbers(a, b) {
const maxLength = Math.max(a.length, b.length);
a = a.padStart(maxLength, "0");
b = b.padStart(maxLength, "0");
let result = "";
let borrow = 0;
for (let i = maxLength - 1; i >= 0; i--) {
let diff = parseInt(a[i]) - parseInt(b[i]) - borrow;
if (diff
<pre class="brush:php;toolbar:false">node multiply.js
Key Features of the Implementation
-
Base Case Optimization:
- For numbers up to 12 digits, the algorithm directly uses JavaScript's Number for efficient multiplication.
-
String Manipulation for Arbitrary Precision:
- The algorithm uses string operations to handle large numbers without losing precision.
-
Helper Functions:
- Addition (addLargeNumbers): Handles the addition of two large numbers represented as strings.
- Subtraction (subtractLargeNumbers): Manages subtraction with borrowing for large numbers.
- Power of 10 Multiplication (multiplyByPowerOf10): Efficiently shifts numbers by appending zeros.
-
Recursive Design:
- The algorithm divides each input recursively, combining results using the Karatsuba formula.
Performance Considerations
The Karatsuba algorithm reduces the number of recursive multiplications from (O(n2)) to approximately (O(n1.585)) . This makes it significantly faster than traditional methods for large inputs. However, the overhead of string manipulations can affect performance for smaller inputs, which is why the base case optimization is crucial.
Example Output
For:
/**
* Karatsuba multiplication algorithm for large numbers.
* @param {string} num1 - First large number as a string.
* @param {string} num2 - Second large number as a string.
* @returns {string} - Product of the two numbers as a string.
*/
function karatsubaMultiply(num1, num2) {
// Remove leading zeros
num1 = num1.replace(/^0+/, "") || "0";
num2 = num2.replace(/^0+/, "") || "0";
// If either number is zero, return "0"
if (num1 === "0" || num2 === "0") return "0";
// Base case for small numbers (12), use Number for safe multiplication
if (num1.length = 0; i--) {
const sum = parseInt(a[i]) + parseInt(b[i]) + carry;
result = (sum % 10) + result;
carry = Math.floor(sum / 10);
}
if (carry > 0) {
result = carry + result;
}
return result.replace(/^0+/, "") || "0";
}
// Helper function to multiply by 10^n
function multiplyByPowerOf10(num, power) {
return num === "0" ? "0" : num + "0".repeat(power);
}
// Helper function for subtracting large numbers
function subtractLargeNumbers(a, b) {
const maxLength = Math.max(a.length, b.length);
a = a.padStart(maxLength, "0");
b = b.padStart(maxLength, "0");
let result = "";
let borrow = 0;
for (let i = maxLength - 1; i >= 0; i--) {
let diff = parseInt(a[i]) - parseInt(b[i]) - borrow;
if (diff
<p>The result is:<br>
</p>
<pre class="brush:php;toolbar:false">node multiply.js
Conclusion
The Karatsuba multiplication algorithm is a practical and efficient solution for multiplying large numbers. This implementation demonstrates its power and flexibility when handling arbitrarily large inputs in JavaScript. With the growing need for high-precision arithmetic, mastering such algorithms can greatly enhance computational capabilities in diverse applications.
The above is the detailed content of Understanding and Implementing the Karatsuba Multiplication Algorithm for Large Numbers. For more information, please follow other related articles on the PHP Chinese website!
 Replace String Characters in JavaScriptMar 11, 2025 am 12:07 AM
Replace String Characters in JavaScriptMar 11, 2025 am 12:07 AMDetailed explanation of JavaScript string replacement method and FAQ This article will explore two ways to replace string characters in JavaScript: internal JavaScript code and internal HTML for web pages. Replace string inside JavaScript code The most direct way is to use the replace() method: str = str.replace("find","replace"); This method replaces only the first match. To replace all matches, use a regular expression and add the global flag g: str = str.replace(/fi
 Custom Google Search API Setup TutorialMar 04, 2025 am 01:06 AM
Custom Google Search API Setup TutorialMar 04, 2025 am 01:06 AMThis tutorial shows you how to integrate a custom Google Search API into your blog or website, offering a more refined search experience than standard WordPress theme search functions. It's surprisingly easy! You'll be able to restrict searches to y
 8 Stunning jQuery Page Layout PluginsMar 06, 2025 am 12:48 AM
8 Stunning jQuery Page Layout PluginsMar 06, 2025 am 12:48 AMLeverage jQuery for Effortless Web Page Layouts: 8 Essential Plugins jQuery simplifies web page layout significantly. This article highlights eight powerful jQuery plugins that streamline the process, particularly useful for manual website creation
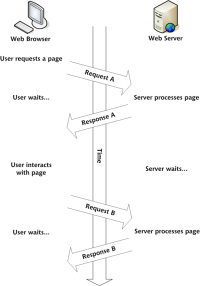 Build Your Own AJAX Web ApplicationsMar 09, 2025 am 12:11 AM
Build Your Own AJAX Web ApplicationsMar 09, 2025 am 12:11 AMSo here you are, ready to learn all about this thing called AJAX. But, what exactly is it? The term AJAX refers to a loose grouping of technologies that are used to create dynamic, interactive web content. The term AJAX, originally coined by Jesse J
 What is 'this' in JavaScript?Mar 04, 2025 am 01:15 AM
What is 'this' in JavaScript?Mar 04, 2025 am 01:15 AMCore points This in JavaScript usually refers to an object that "owns" the method, but it depends on how the function is called. When there is no current object, this refers to the global object. In a web browser, it is represented by window. When calling a function, this maintains the global object; but when calling an object constructor or any of its methods, this refers to an instance of the object. You can change the context of this using methods such as call(), apply(), and bind(). These methods call the function using the given this value and parameters. JavaScript is an excellent programming language. A few years ago, this sentence was
 Improve Your jQuery Knowledge with the Source ViewerMar 05, 2025 am 12:54 AM
Improve Your jQuery Knowledge with the Source ViewerMar 05, 2025 am 12:54 AMjQuery is a great JavaScript framework. However, as with any library, sometimes it’s necessary to get under the hood to discover what’s going on. Perhaps it’s because you’re tracing a bug or are just curious about how jQuery achieves a particular UI
 10 Mobile Cheat Sheets for Mobile DevelopmentMar 05, 2025 am 12:43 AM
10 Mobile Cheat Sheets for Mobile DevelopmentMar 05, 2025 am 12:43 AMThis post compiles helpful cheat sheets, reference guides, quick recipes, and code snippets for Android, Blackberry, and iPhone app development. No developer should be without them! Touch Gesture Reference Guide (PDF) A valuable resource for desig
 How do I create and publish my own JavaScript libraries?Mar 18, 2025 pm 03:12 PM
How do I create and publish my own JavaScript libraries?Mar 18, 2025 pm 03:12 PMArticle discusses creating, publishing, and maintaining JavaScript libraries, focusing on planning, development, testing, documentation, and promotion strategies.


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

PhpStorm Mac version
The latest (2018.2.1) professional PHP integrated development tool

Zend Studio 13.0.1
Powerful PHP integrated development environment

SublimeText3 Mac version
God-level code editing software (SublimeText3)

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),





