Investigating the performance of np.einsum

A reader of my last blog post pointed out to me that for slicewise matmul-like operations, np.einsum is considerably slower than np.matmul unless you turn on the optimize flag in the parameters list: np.einsum(..., optimize = True).

Being somewhat skeptical, I fired up a Jupyter notebook and did some preliminary tests. And I'll be damned, it's completely true - even for two-operand cases where optimize shouldn't make any difference at all!

Test 1 is pretty simple - matrix multiplication of two C-order (aka row major order) matrices of varying dimensions. np.matmul is consistently about twenty times faster.

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.765	0.045	17.055
(100, 1000)	(1000, 100)	1.495	0.073	20.554
(100, 10000)	(10000, 100)	15.148	0.896	16.899

For Test 2, with optimize=True, the results are drastically different. np.einsum is still slower, but only about 1.5 times slower at worst!

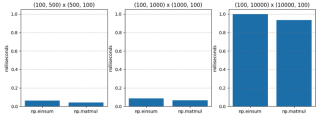
M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	0.063	0.043	1.474
(100, 1000)	(1000, 100)	0.086	0.067	1.284
(100, 10000)	(10000, 100)	1.000	0.936	1.068

Why?

My understanding of the optimize flag is that it determines an optimal contraction order when there are three or more operands. Here, we have only two operands. So optimize shouldn't make a difference, right?

But maybe optimize is doing something more than just picking a contraction order? Maybe optimize is aware of memory layout, and this has something to do with row-major vs. column-major layout?

In the grade-school method of matrix multiplication, to calculate a single entry, you iterate over a row in op1 while you iterate over a column in op2, so putting the second argument in column-major order might result in a speedup for np.einsum (assuming that np.einsum is sort of like a generalized version of the grade-school method of matrix multiplication under the hood, which I suspect is true).

So, for Test 3, I passed in a column-major matrix for the second operand to see if this sped up np.einsum when optimize=False.

Here are the results. Surprisingly, np.einsum is still considerably worse. Clearly, something is going on that I don't understand - perhaps np.einsum uses an entirely different code-path when optimize is True? Time to start digging.

M1	M2	np.einsum	np.matmul	np.einsum / np.matmul
(100, 500)	(500, 100)	1.486	0.056	26.541
(100, 1000)	(1000, 100)	3.885	0.125	31.070
(100, 10000)	(10000, 100)	49.669	1.047	47.444

Going Deeper

The release notes of Numpy 1.12.0 mention the introduction of the optimize flag. However, the purpose of optimize seems to be to determine the order that arguments in a chain of operands are combined (i.e.; the associativity) - so optimize shouldn't make a difference for just two operands, right? Here's the release notes:

np.einsum now supports the optimize argument which will optimize the order of contraction. For example, np.einsum would complete the chain dot example np.einsum(‘ij,jk,kl->il’, a, b, c) in a single pass which would scale like N^4; however, when optimize=True np.einsum will create an intermediate array to reduce this scaling to N^3 or effectively np.dot(a, b).dot(c). Usage of intermediate tensors to reduce scaling has been applied to the general einsum summation notation. See np.einsum_path for more details.

To compound the mystery, some later release notes indicate that np.einsum was upgraded to use tensordot (which itself uses BLAS where appropriate). Now, that seems promising.

But then, why are we only seeing the speedup when optimize is True? What's going on?

If we read def einsum(*operands, out=None, optimize=False, **kwargs) in numpy/numpy/_core/einsumfunc.py, we'll come to this early-out logic almost immediately:

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

Does c_einsum utilize tensordot? I doubt it. Later on in the code, we see the tensordot call that the 1.14 notes seem to be referencing:

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

So, here's what's happening:

1. The contraction_list loop is executed if optimize is True - even in the trivial two operand case.
2. tensordot is only invoked in the contraction_list loop.
3. Therefore, we invoke tensordot (and therefore BLAS) when optimize is True.

To me, this seems like a bug. IMHO, the "early-out" at the beginning of np.einsum should still detect if the operands are tensordot-compatible and call out to tensordot if possible. Then, we would get the obvious BLAS speedups even when optimize is False. After all, the semantics of optimize pertain to contraction order, not to usage of BLAS, which I think should be a given.

The boon here is that persons invoking np.einsum for operations that are equivalent to a tensordot invocation would get the appropriate speedups, which makes np.einsum a bit less dangerous from a performance point of view.

How does c_einsum actually work?

I spelunked some C code to check it out. The heart of the implementation is here.

After a great deal of argument parsing and parameter preparation, the axis iteration order is determined and a special-purpose iterator is prepared. Each yield from the iterator represents a different way to stride over all operands simultaneously.

    # If no optimization, run pure einsum
    if optimize is False:
        if specified_out:
            kwargs['out'] = out
        return c_einsum(*operands, **kwargs)

Assuming certain special-case optimizations don't apply, an appropriate sum-of-products (sop) function is determined based on the datatypes involved:

    # Start contraction loop
    for num, contraction in enumerate(contraction_list):

        ...

        # Call tensordot if still possible
        if blas:

            ...

            # Contract!
            new_view = tensordot(
                *tmp_operands, axes=(tuple(left_pos), tuple(right_pos))
            )

And then, this sum-of-products (sop) operation is invoked on each multi-operand stride returned from the iterator, as seen here:

    /* Allocate the iterator */
    iter = NpyIter_AdvancedNew(nop+1, op, iter_flags, order, casting, op_flags,
                               op_dtypes, ndim_iter, op_axes, NULL, 0);

That's my understanding of how einsum works, which is admittedly still a little thin - it really deserves more than the hour I've given it.

But it does confirm my suspicions, however, that it acts like a generalized, gigabrain version of the grade-school method of matrix multiplication. Ultimately, it delegates out to a series of "sum of product" operations which rely on "striders" moving through the operands - not too different from what you do with your fingers when you learn matrix multiplication.

Summary

So why is np.einsum generally faster when you call it with optimize=True? There are two reasons.

The first (and original) reason is it tries to find an optimal contraction path. However, as I pointed out, that shouldn't matter when we have just two operands, as we do in our performance tests.

The second (and newer) reason is that when optimize=True, even in the two operand case it activates a codepath that calls tensordot where possible, which in turn tries to use BLAS. And BLAS is as optimized as matrix multiplication gets!

So, the two-operands speedup mystery is solved! However, we haven't really covered the characteristics of the speedup due to contraction order. That will have to wait for a future post! Stay tuned!

The above is the detailed content of Investigating the performance of np.einsum. For more information, please follow other related articles on the PHP Chinese website!