 Backend Development
Backend Development PHP Tutorial
PHP Tutorial The Curse of atan() and the Story of atan: A Story of Disorientation in the Coding World
The Curse of atan() and the Story of atan: A Story of Disorientation in the Coding World
Hello Coders Pirates ?☠️ Have you ever found yourself lost in the coding sea, just trying to figure out the angle using atan(), and frustrated that you can't find the right direction. you are not alone Today we are going on an adventure, where we will find the treasure called atan2() in PHP. Let's see why atan() can put you in danger, while atan2() will get you safely to port.
Let's start the journey then. ⛵
Imagine you have a treasure map. There is talk of an island, which is navigated to a point (x, y) on the map. You can use atan()—but stop! It is only part of the story. atan() can take you straight to Davy Jones' locker, or worse, to a codebase full of bugs. ? So if you want to get the right path, you need atan2(), the Captain Jack Sparrow of this story.
The story of atan()'s curse
This atan() function can be found in almost all languages. We talk about php. atan() is mainly used to calculate angles. But here's a problem — atan() only cares about the y/x ratio, it doesn't care what quadrant you're in. If you start trusting him completely, you may find that you are going in the wrong direction. Why? Because atan() doesn't return the whole image—it only tells the angle relative to the first quadrant.
Why? Because atan() doesn't give the whole image — it only tells the angle relative to the first quadrant. That means when you are going west, you should actually be traveling east! atan2(), on the other hand, takes both x and y coordinates into account, and—like a good compass—knows exactly which quadrant you're in.
Now let's know a little more about the difference between these 2.
Difference between atan() and atan2()
Now let's say it in code language:
- atan() calculates the arctangent of the ratio y/x, but doesn't know the whole image. Is the target in the second quadrant? Third? atan() has no idea and doesn't even bother.
The parameter of the atan() function is a number, which is the value of the ratio y/x, where y and x are two variables or number values.
atan(float $num): float
- On the other hand, atan2() knows exactly where the (x, y) point is and returns the correct angle in any quadrant.
The parameters ofatan2() function are 2.
- $y: Y coordinate value.
- $x: X coordinate value.
atan2(float $y, float $x): float
Let's try to understand the matter with an example.
// $y এবং $x এর মান নির্ধারণ $y = 5; $x = -10; // atan() ব্যবহার - শুধুমাত্র y/x অনুপাত জানে $angle1 = atan($y / $x); echo "atan() angle: " . rad2deg($angle1) . " degrees\n"; // Outputs: -26.57 degrees // atan2() ব্যবহার - $x এবং $y উভয়ই বিবেচনায় নেয় $angle2 = atan2($y, $x); echo "atan2() angle: " . rad2deg($angle2) . " degrees\n"; // Outputs: 153.43 degrees
As you can see from the example, atan() does return an angle. But the direction is not telling. That is, it is not understood which quadrant you are in. On the other hand, the value we get with the atan2() function clearly shows that the point (x, which) is in the 2nd quadrant. Now we can easily understand which direction the treasure island is.
?Radians vs Degrees (It's not just math, it's living!)
PHP's atan() and atan2() functions give you an angle in radians. Which looks like a joke! Don't worry—it's just a different method of measuring angles. For humans and pirates to understand, I converted it to degrees using the rad2deg() function.
My own atan() and atan2()
Let us now try to make atan() and atan2() our own, to better understand their operation.
⚠️ If you feel like this is going over your head, skip this section! ?
Let's create atan()
atan() calculates the arctangent of a number. One way to approximate this function is to use Gregory's series. Here is a commonly used series for atan(z):
which if written a little straighter stands -
Now let's write this series in code
atan(float $num): float
Let's create atan2()
Now we will use the atan() function to createatan2(). The main task of this function is to identify the correct quadrant only. So why delay, let's write -
atan2(float $y, float $x): float
Let me tell you the whole story now
Now we look at the four quadrant results and explain each quadrant:
- First Quadrant (Quadrant I): when x=10 And y=5 Then atan($y / $x) is 26.57 degrees and atan2($y, $x) is 26.56 degrees. Here in both cases it is in the first quarter.
- Second Quadrant (Quadrant II): when x=−10 And y=5 Then atan($y / $x) is -26.57 degrees and atan2($y, $x) is 153.43 degrees. Here atan2() is clearly indicating the second quarter.
- Third Quadrant (Quadrant III): when x=−10 And y=−5 Then atan($y / $x) is -26.57 degrees and atan2($y, $x) is -233.43 degrees. It is in the third quarter.
- Fourth Quadrant (Quadrant IV): when x=10 And y=−5 Then atan($y / $x) is -26.57 degrees and atan2($y, $x) is -26.56 degrees. Here it is in the fourth quarter.
☠️ Learning from mistakes
So next time you're navigating the dangerous ocean of angles and coordinates, don't just rely on atan(). Use atan2() and steer your ship in the right direction every time. It's the compass that will keep you out of the dreaded Davy Jones locker of miscalculations!
Hope your treasure journey goes well.
If you want to know more about atan() and atan2(), visit the following links:
- https://www.php.net/manual/en/function.atan.php
- https://www.php.net/manual/en/function.atan2.php
The above is the detailed content of The Curse of atan() and the Story of atan: A Story of Disorientation in the Coding World. For more information, please follow other related articles on the PHP Chinese website!
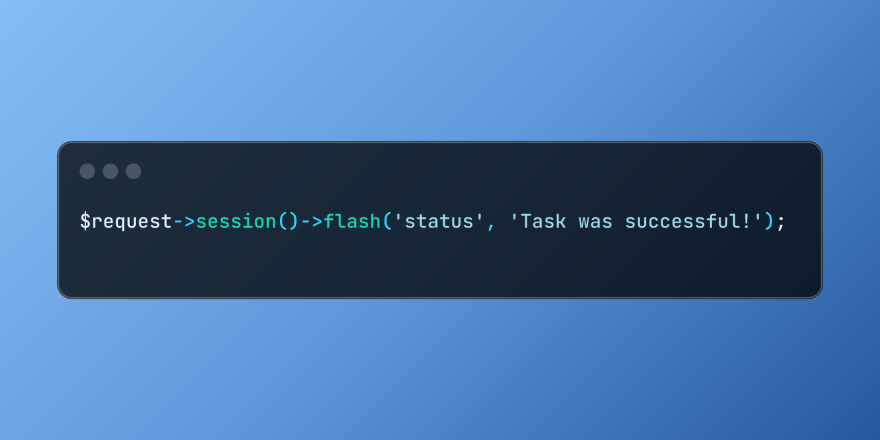 Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PM
Working with Flash Session Data in LaravelMar 12, 2025 pm 05:08 PMLaravel simplifies handling temporary session data using its intuitive flash methods. This is perfect for displaying brief messages, alerts, or notifications within your application. Data persists only for the subsequent request by default: $request-
 cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AM
cURL in PHP: How to Use the PHP cURL Extension in REST APIsMar 14, 2025 am 11:42 AMThe PHP Client URL (cURL) extension is a powerful tool for developers, enabling seamless interaction with remote servers and REST APIs. By leveraging libcurl, a well-respected multi-protocol file transfer library, PHP cURL facilitates efficient execution of various network protocols, including HTTP, HTTPS, and FTP. This extension offers granular control over HTTP requests, supports multiple concurrent operations, and provides built-in security features.
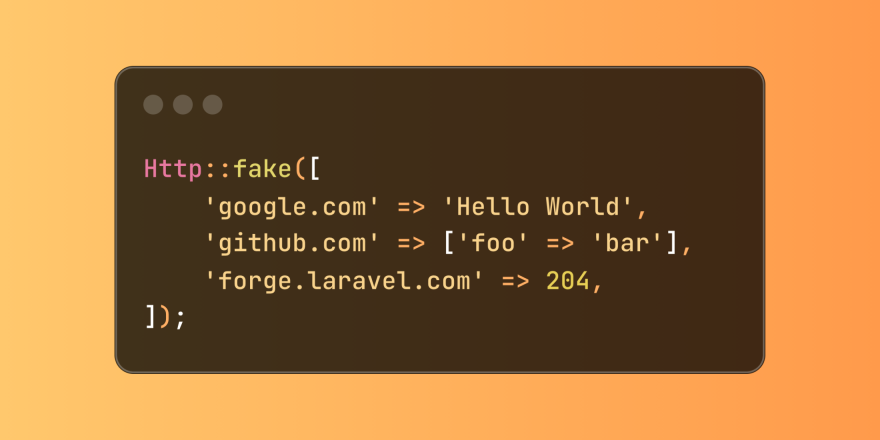 Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PM
Simplified HTTP Response Mocking in Laravel TestsMar 12, 2025 pm 05:09 PMLaravel provides concise HTTP response simulation syntax, simplifying HTTP interaction testing. This approach significantly reduces code redundancy while making your test simulation more intuitive. The basic implementation provides a variety of response type shortcuts: use Illuminate\Support\Facades\Http; Http::fake([ 'google.com' => 'Hello World', 'github.com' => ['foo' => 'bar'], 'forge.laravel.com' =>
 12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PM
12 Best PHP Chat Scripts on CodeCanyonMar 13, 2025 pm 12:08 PMDo you want to provide real-time, instant solutions to your customers' most pressing problems? Live chat lets you have real-time conversations with customers and resolve their problems instantly. It allows you to provide faster service to your custom
 PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PM
PHP Logging: Best Practices for PHP Log AnalysisMar 10, 2025 pm 02:32 PMPHP logging is essential for monitoring and debugging web applications, as well as capturing critical events, errors, and runtime behavior. It provides valuable insights into system performance, helps identify issues, and supports faster troubleshoot
 Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PM
Explain the concept of late static binding in PHP.Mar 21, 2025 pm 01:33 PMArticle discusses late static binding (LSB) in PHP, introduced in PHP 5.3, allowing runtime resolution of static method calls for more flexible inheritance.Main issue: LSB vs. traditional polymorphism; LSB's practical applications and potential perfo
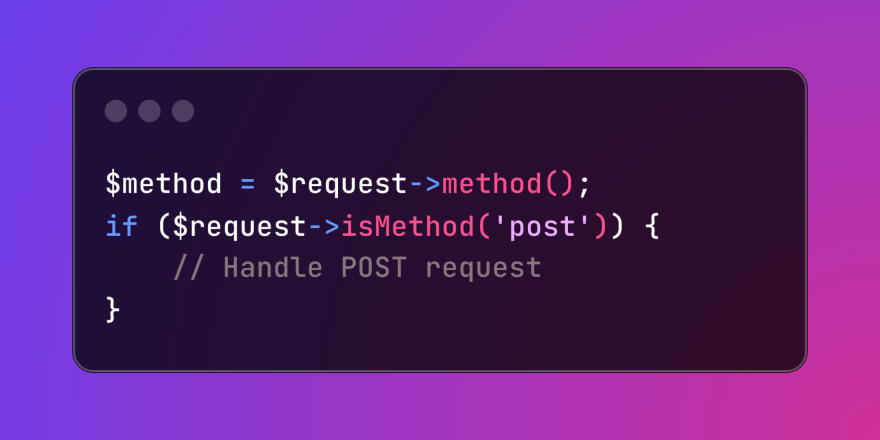 HTTP Method Verification in LaravelMar 05, 2025 pm 04:14 PM
HTTP Method Verification in LaravelMar 05, 2025 pm 04:14 PMLaravel simplifies HTTP verb handling in incoming requests, streamlining diverse operation management within your applications. The method() and isMethod() methods efficiently identify and validate request types. This feature is crucial for building
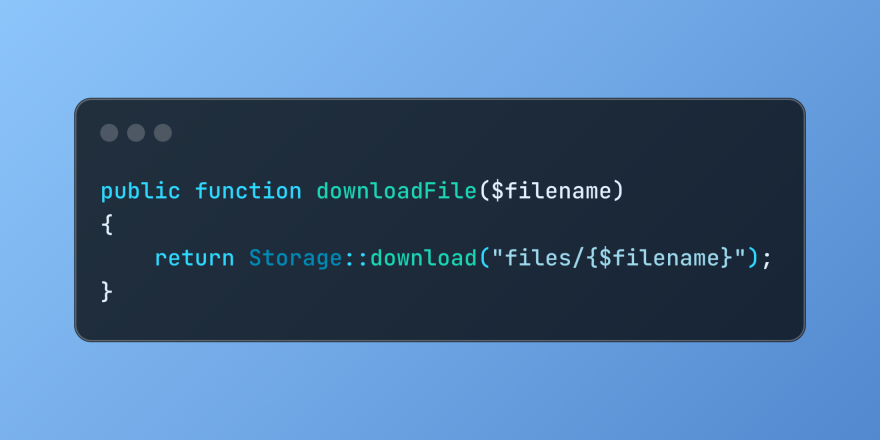 Discover File Downloads in Laravel with Storage::downloadMar 06, 2025 am 02:22 AM
Discover File Downloads in Laravel with Storage::downloadMar 06, 2025 am 02:22 AMThe Storage::download method of the Laravel framework provides a concise API for safely handling file downloads while managing abstractions of file storage. Here is an example of using Storage::download() in the example controller:


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

MantisBT
Mantis is an easy-to-deploy web-based defect tracking tool designed to aid in product defect tracking. It requires PHP, MySQL and a web server. Check out our demo and hosting services.

Atom editor mac version download
The most popular open source editor

Dreamweaver Mac version
Visual web development tools

Notepad++7.3.1
Easy-to-use and free code editor

SublimeText3 English version
Recommended: Win version, supports code prompts!





