Home >Backend Development >PHP Tutorial >Path with Maximum Probability
Path with Maximum Probability
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2024-08-28 06:40:37766browse
1514. Path with Maximum Probability
Difficulty: Medium
Topics: Array, Graph, Heap (Priority Queue), Shortest Path
You are given an undirected weighted graph of n nodes (0-indexed), represented by an edge list where edges[i] = [a, b] is an undirected edge connecting the nodes a and b with a probability of success of traversing that edge succProb[i].
Given two nodes start and end, find the path with the maximum probability of success to go from start to end and return its success probability.
If there is no path from start to end, return 0. Your answer will be accepted if it differs from the correct answer by at most 1e-5.
Example 1:
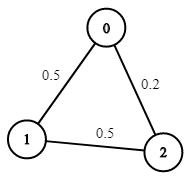
- Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.2], start = 0, end = 2
- Output: 0.25000
- Explanation: There are two paths from start to end, one having a probability of success = 0.2 and the other has 0.5 * 0.5 = 0.25.
Example 2:
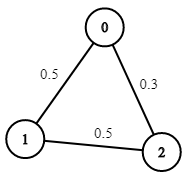
- Input: n = 3, edges = [[0,1],[1,2],[0,2]], succProb = [0.5,0.5,0.3], start = 0, end = 2
- Output: 0.30000
Example 3:
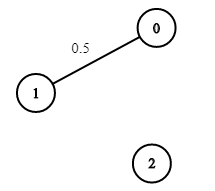
- Input: n = 3, edges = [[0,1]], succProb = [0.5], start = 0, end = 2
- Output: 0.00000
- Explanation: There is no path between 0 and 2.
Constraints:
- 2 <= n <= 10^4
- 0 <= start, end < n
- start != end
- 0 <= a, b < n
- a != b
- 0 <= succProb.length == edges.length <= 2*10^4
- 0 <= succProb[i] <= 1
- There is at most one edge between every two nodes
Hint:
- Multiplying probabilities will result in precision errors.
- Take log probabilities to sum up numbers instead of multiplying them.
- Use Dijkstra's algorithm to find the minimum path between the two nodes after negating all costs.
Solution:
We can use a modified version of Dijkstra's algorithm. Instead of finding the shortest path, you'll be maximizing the probability of success.
Let's implement this solution in PHP: 1514. Path with Maximum Probability
<?php
/**
* @param Integer $n
* @param Integer[][] $edges
* @param Float[] $succProb
* @param Integer $start_node
* @param Integer $end_node
* @return Float
*/
function maxProbability($n, $edges, $succProb, $start_node, $end_node) {
...
...
...
/**
* go to ./solution.php
*/
}
// Example usage:
$n1 = 3;
$edges1 = [[0,1],[1,2],[0,2]];
$succProb1 = [0.5,0.5,0.2];
$start_node1 = 0;
$end_node1 = 2;
echo maxProbability($n1, $edges1, $succProb1, $start_node1, $end_node1);//Output: 0.25000
$n2 = 3;
$edges2 = [[0,1],[1,2],[0,2]];
$succProb2 = [0.5,0.5,0.3];
$start_node2 = 0;
$end_node2 = 2;
echo maxProbability($n2, $edges2, $succProb2, $start_node2, $end_node2);//Output: 0.30000
$n3 = 3;
$edges3 = [[0,1]];
$succProb3 = [0.5;
$start_node3 = 0;
$end_node3 = 2;
echo maxProbability($n3, $edges3, $succProb3, $start_node3, $end_node3); //Output: 0.00000
?>
<h3>
Explanation:
</h3>
<ol>
<li><p><strong>Graph Representation</strong>: The graph is represented as an adjacency list where each node points to its neighbors along with the success probabilities of the edges connecting them.</p></li>
<li><p><strong>Max Probability Array</strong>: An array maxProb is used to store the maximum probability to reach each node from the start node.</p></li>
<li><p><strong>Priority Queue</strong>: A max heap (SplPriorityQueue) is used to explore paths with the highest probability first. This is crucial to ensure that when we reach the destination node, we've found the path with the maximum probability.</p></li>
<li>
<p><strong>Algorithm</strong>:</p>
<ul>
<li>Initialize the start node's probability as 1 (since the probability of staying at the start is 1).</li>
<li>Use the priority queue to explore nodes, updating the maximum probability to reach each neighbor.</li>
<li>If the destination node is reached, return the probability.</li>
<li>If no path exists, return 0.</li>
</ul>
</li>
</ol>
<h3>
Output:
</h3>
<p>For the example provided:<br>
</p>
<pre class="brush:php;toolbar:false">$n = 3;
$edges = [[0,1],[1,2],[0,2]];
$succProb = [0.5,0.5,0.2];
$start_node = 0;
$end_node = 2;
The output will be 0.25.
This approach ensures an efficient solution using Dijkstra's algorithm while handling the specifics of probability calculations.
Contact Links
If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks ?. Your support would mean a lot to me!
If you want more helpful content like this, feel free to follow me:
- GitHub
The above is the detailed content of Path with Maximum Probability. For more information, please follow other related articles on the PHP Chinese website!

