 Technology peripherals
Technology peripherals AI
AI Unlimited video generation, planning and decision-making, diffusion forced integration of next token prediction and full sequence diffusion
Unlimited video generation, planning and decision-making, diffusion forced integration of next token prediction and full sequence diffusionCurrently, autoregressive large-scale language models using the next token prediction paradigm have become popular all over the world. At the same time, a large number of synthetic images and videos on the Internet have already shown us the power of diffusion models.
Recently, a research team at MIT CSAIL (one of whom is Chen Boyuan, a PhD student at MIT) successfully integrated the powerful capabilities of the full sequence diffusion model and the next token model, and proposed a training and sampling paradigm: Diffusion Forcing(DF).

Paper title: Diffusion Forcing: Next-token Prediction Meets Full-Sequence Diffusion
Paper address: https://arxiv.org/pdf/2407.01392
Project website: https://arxiv.org/pdf/2407.01392 /boyuan.space/diffusion-forcing
Code address: https://github.com/buoyancy99/diffusion-forcing
As shown below, diffusion forcing clearly outperforms all in terms of consistency and stability Two methods are sequence diffusion and teacher forcing.

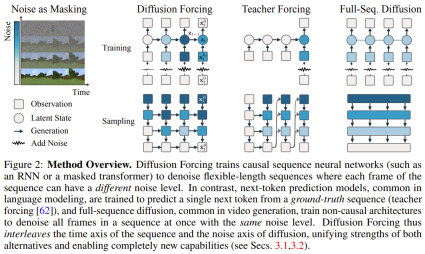

 ) as a kind of partial masking, which can be called "performing masking along the noise axis".
) as a kind of partial masking, which can be called "performing masking along the noise axis".  is (probably) white noise, and there is no longer any information about the original data. As shown in Figure 2, the team established a unified perspective to look at the edge. Masks for these two axes.
is (probably) white noise, and there is no longer any information about the original data. As shown in Figure 2, the team established a unified perspective to look at the edge. Masks for these two axes.  This paper focuses on time series data, so they instantiate DF through a causal architecture, and thus get. Causal diffusion forcing (CDF). Simply put, this is a minimal implementation obtained using a basic recurrent neural network (RNN). An RNN with weight θ maintains a hidden state z_t that is informed of the influence of past tokens. It will evolve according to the dynamic
This paper focuses on time series data, so they instantiate DF through a causal architecture, and thus get. Causal diffusion forcing (CDF). Simply put, this is a minimal implementation obtained using a basic recurrent neural network (RNN). An RNN with weight θ maintains a hidden state z_t that is informed of the influence of past tokens. It will evolve according to the dynamic  is obtained, the hidden state is updated in a Markovian manner.
is obtained, the hidden state is updated in a Markovian manner. 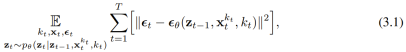

 , where the expected value is averaged over the noise level and
, where the expected value is averaged over the noise level and  is noisy according to a forward process. In addition, under appropriate conditions, optimizing (3.1) can also maximize the lower likelihood limit of all noise level sequences simultaneously.
is noisy according to a forward process. In addition, under appropriate conditions, optimizing (3.1) can also maximize the lower likelihood limit of all noise level sequences simultaneously. 
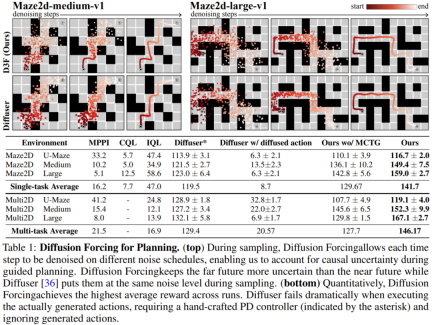
Stable autoregressive generation Keep the future uncertain Long-term guidance capability
 . Here the token x_t = [a_t, r_t, o_{t+1}] is allocated. A trajectory is a sequence x_{1:T}, whose length may be variable; the training method is as shown in Algorithm 1.
. Here the token x_t = [a_t, r_t, o_{t+1}] is allocated. A trajectory is a sequence x_{1:T}, whose length may be variable; the training method is as shown in Algorithm 1.  is sampled according to Algorithm 2, where
is sampled according to Algorithm 2, where  contains predicted actions, rewards and observations. H is a forward observation window, similar to future predictions in model predictive control. After taking the planned action, the environment gets a reward and the next observation, and thus the next token. The hidden state can be updated according to the posterior p_θ(z_t|z_{t−1}, x_t, 0).
contains predicted actions, rewards and observations. H is a forward observation window, similar to future predictions in model predictive control. After taking the planned action, the environment gets a reward and the next observation, and thus the next token. The hidden state can be updated according to the posterior p_θ(z_t|z_{t−1}, x_t, 0). with flexible planning horizons enables flexible reward guidance can be achieved Monte Carlo Tree Guidance (MCTG) to achieve future uncertainty




The above is the detailed content of Unlimited video generation, planning and decision-making, diffusion forced integration of next token prediction and full sequence diffusion. For more information, please follow other related articles on the PHP Chinese website!
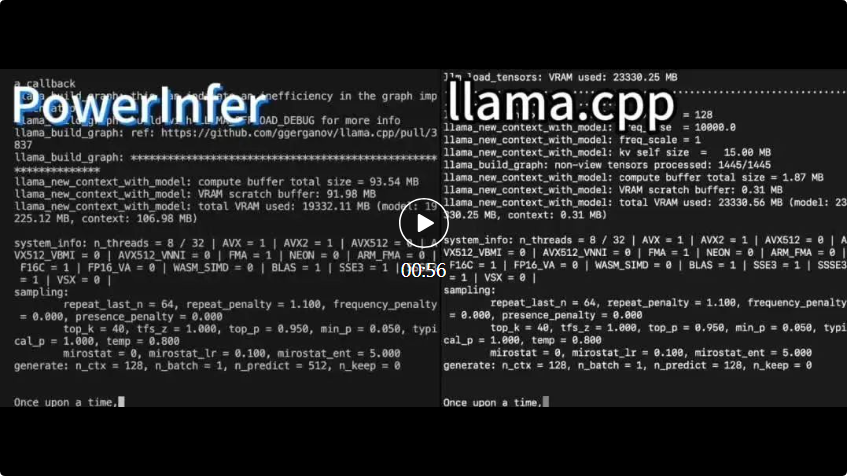 4090生成器:与A100平台相比,token生成速度仅低于18%,上交推理引擎赢得热议Dec 21, 2023 pm 03:25 PM
4090生成器:与A100平台相比,token生成速度仅低于18%,上交推理引擎赢得热议Dec 21, 2023 pm 03:25 PMPowerInfer提高了在消费级硬件上运行AI的效率上海交大团队最新推出了超强CPU/GPULLM高速推理引擎PowerInfer。PowerInfer和llama.cpp都在相同的硬件上运行,并充分利用了RTX4090上的VRAM。这个推理引擎速度有多快?在单个NVIDIARTX4090GPU上运行LLM,PowerInfer的平均token生成速率为13.20tokens/s,峰值为29.08tokens/s,仅比顶级服务器A100GPU低18%,可适用于各种LLM。PowerInfer与
 思维链CoT进化成思维图GoT,比思维树更优秀的提示工程技术诞生了Sep 05, 2023 pm 05:53 PM
思维链CoT进化成思维图GoT,比思维树更优秀的提示工程技术诞生了Sep 05, 2023 pm 05:53 PM要让大型语言模型(LLM)充分发挥其能力,有效的prompt设计方案是必不可少的,为此甚至出现了promptengineering(提示工程)这一新兴领域。在各种prompt设计方案中,思维链(CoT)凭借其强大的推理能力吸引了许多研究者和用户的眼球,基于其改进的CoT-SC以及更进一步的思维树(ToT)也收获了大量关注。近日,苏黎世联邦理工学院、Cledar和华沙理工大学的一个研究团队提出了更进一步的想法:思维图(GoT)。让思维从链到树到图,为LLM构建推理过程的能力不断得到提升,研究者也通
 复旦NLP团队发布80页大模型Agent综述,一文纵览AI智能体的现状与未来Sep 23, 2023 am 09:01 AM
复旦NLP团队发布80页大模型Agent综述,一文纵览AI智能体的现状与未来Sep 23, 2023 am 09:01 AM近期,复旦大学自然语言处理团队(FudanNLP)推出LLM-basedAgents综述论文,全文长达86页,共有600余篇参考文献!作者们从AIAgent的历史出发,全面梳理了基于大型语言模型的智能代理现状,包括:LLM-basedAgent的背景、构成、应用场景、以及备受关注的代理社会。同时,作者们探讨了Agent相关的前瞻开放问题,对于相关领域的未来发展趋势具有重要价值。论文链接:https://arxiv.org/pdf/2309.07864.pdfLLM-basedAgent论文列表:
 FATE 2.0发布:实现异构联邦学习系统互联Jan 16, 2024 am 11:48 AM
FATE 2.0发布:实现异构联邦学习系统互联Jan 16, 2024 am 11:48 AMFATE2.0全面升级,推动隐私计算联邦学习规模化应用FATE开源平台宣布发布FATE2.0版本,作为全球领先的联邦学习工业级开源框架。此次更新实现了联邦异构系统之间的互联互通,持续增强了隐私计算平台的互联互通能力。这一进展进一步推动了联邦学习与隐私计算规模化应用的发展。FATE2.0以全面互通为设计理念,采用开源方式对应用层、调度、通信、异构计算(算法)四个层面进行改造,实现了系统与系统、系统与算法、算法与算法之间异构互通的能力。FATE2.0的设计兼容了北京金融科技产业联盟的《金融业隐私计算
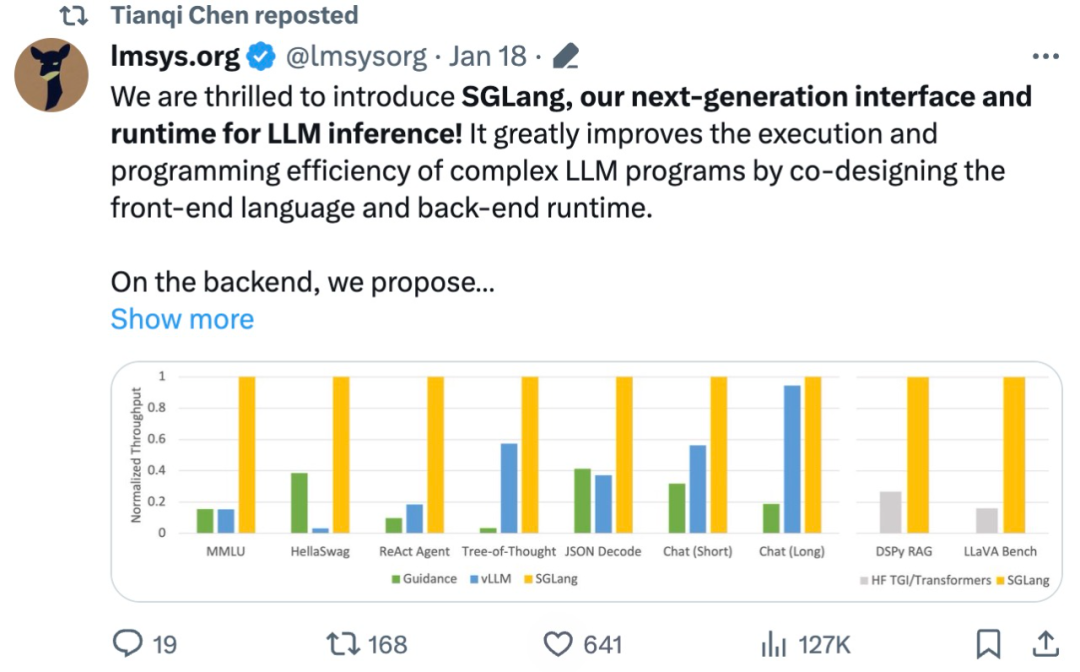 吞吐量提升5倍,联合设计后端系统和前端语言的LLM接口来了Mar 01, 2024 pm 10:55 PM
吞吐量提升5倍,联合设计后端系统和前端语言的LLM接口来了Mar 01, 2024 pm 10:55 PM大型语言模型(LLM)被广泛应用于需要多个链式生成调用、高级提示技术、控制流以及与外部环境交互的复杂任务。尽管如此,目前用于编程和执行这些应用程序的高效系统却存在明显的不足之处。研究人员最近提出了一种新的结构化生成语言(StructuredGenerationLanguage),称为SGLang,旨在改进与LLM的交互性。通过整合后端运行时系统和前端语言的设计,SGLang使得LLM的性能更高、更易控制。这项研究也获得了机器学习领域的知名学者、CMU助理教授陈天奇的转发。总的来说,SGLang的
 大模型也有小偷?为保护你的参数,上交大给大模型制作「人类可读指纹」Feb 02, 2024 pm 09:33 PM
大模型也有小偷?为保护你的参数,上交大给大模型制作「人类可读指纹」Feb 02, 2024 pm 09:33 PM将不同的基模型象征为不同品种的狗,其中相同的「狗形指纹」表明它们源自同一个基模型。大模型的预训练需要耗费大量的计算资源和数据,因此预训练模型的参数成为各大机构重点保护的核心竞争力和资产。然而,与传统软件知识产权保护不同,对预训练模型参数盗用的判断存在以下两个新问题:1)预训练模型的参数,尤其是千亿级别模型的参数,通常不会开源。预训练模型的输出和参数会受到后续处理步骤(如SFT、RLHF、continuepretraining等)的影响,这使得判断一个模型是否基于另一个现有模型微调得来变得困难。无
 220亿晶体管,IBM机器学习专用处理器NorthPole,能效25倍提升Oct 23, 2023 pm 03:13 PM
220亿晶体管,IBM机器学习专用处理器NorthPole,能效25倍提升Oct 23, 2023 pm 03:13 PMIBM再度发力。随着AI系统的飞速发展,其能源需求也在不断增加。训练新系统需要大量的数据集和处理器时间,因此能耗极高。在某些情况下,执行一些训练好的系统,智能手机就能轻松胜任。但是,执行的次数太多,能耗也会增加。幸运的是,有很多方法可以降低后者的能耗。IBM和英特尔已经试验过模仿实际神经元行为设计的处理器。IBM还测试了在相变存储器中执行神经网络计算,以避免重复访问RAM。现在,IBM又推出了另一种方法。该公司的新型NorthPole处理器综合了上述方法的一些理念,并将其与一种非常精简的计算运行
 何恺明和谢赛宁团队成功跟随解构扩散模型探索,最终创造出备受赞誉的去噪自编码器Jan 29, 2024 pm 02:15 PM
何恺明和谢赛宁团队成功跟随解构扩散模型探索,最终创造出备受赞誉的去噪自编码器Jan 29, 2024 pm 02:15 PM去噪扩散模型(DDM)是目前广泛应用于图像生成的一种方法。最近,XinleiChen、ZhuangLiu、谢赛宁和何恺明四人团队对DDM进行了解构研究。通过逐步剥离其组件,他们发现DDM的生成能力逐渐下降,但表征学习能力仍然保持一定水平。这说明DDM中的某些组件对于表征学习的作用可能并不重要。针对当前计算机视觉等领域的生成模型,去噪被认为是一种核心方法。这类方法通常被称为去噪扩散模型(DDM),通过学习一个去噪自动编码器(DAE),能够通过扩散过程有效地消除多个层级的噪声。这些方法实现了出色的图


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

AI Hentai Generator
Generate AI Hentai for free.

Hot Article

Hot Tools

Dreamweaver CS6
Visual web development tools

SecLists
SecLists is the ultimate security tester's companion. It is a collection of various types of lists that are frequently used during security assessments, all in one place. SecLists helps make security testing more efficient and productive by conveniently providing all the lists a security tester might need. List types include usernames, passwords, URLs, fuzzing payloads, sensitive data patterns, web shells, and more. The tester can simply pull this repository onto a new test machine and he will have access to every type of list he needs.

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

EditPlus Chinese cracked version
Small size, syntax highlighting, does not support code prompt function

mPDF
mPDF is a PHP library that can generate PDF files from UTF-8 encoded HTML. The original author, Ian Back, wrote mPDF to output PDF files "on the fly" from his website and handle different languages. It is slower than original scripts like HTML2FPDF and produces larger files when using Unicode fonts, but supports CSS styles etc. and has a lot of enhancements. Supports almost all languages, including RTL (Arabic and Hebrew) and CJK (Chinese, Japanese and Korean). Supports nested block-level elements (such as P, DIV),





