Home >Backend Development >Python Tutorial >K Nearest Neighbors Regression, Regression: Supervised Machine Learning
K Nearest Neighbors Regression, Regression: Supervised Machine Learning
- 王林Original
- 2024-07-17 22:18:41982browse
k-Nearest Neighbors Regression
k-Nearest Neighbors (k-NN) regression is a non-parametric method that predicts the output value based on the average (or weighted average) of the k-nearest training data points in the feature space. This approach can effectively model complex relationships in data without assuming a specific functional form.
The k-NN regression method can be summarized as follows:
- Distance Metric: The algorithm uses a distance metric (commonly Euclidean distance) to determine the "closeness" of data points.
- k Neighbors: The parameter k specifies how many nearest neighbors to consider when making predictions.
- Prediction: The predicted value for a new data point is the average of the values of its k nearest neighbors.
Key Concepts
Non-Parametric: Unlike parametric models, k-NN does not assume a specific form for the underlying relationship between the input features and the target variable. This makes it flexible in capturing complex patterns.
Distance Calculation: The choice of distance metric can significantly affect the model's performance. Common metrics include Euclidean, Manhattan, and Minkowski distances.
Choice of k: The number of neighbors (k) can be chosen based on cross-validation. A small k can lead to overfitting, while a large k can smooth out the prediction too much, potentially underfitting.
k-Nearest Neighbors Regression Example
This example demonstrates how to use k-NN regression with polynomial features to model complex relationships while leveraging the non-parametric nature of k-NN.
Python Code Example
1. Import Libraries
import numpy as np import matplotlib.pyplot as plt from sklearn.model_selection import train_test_split from sklearn.preprocessing import PolynomialFeatures from sklearn.neighbors import KNeighborsRegressor from sklearn.metrics import mean_squared_error, r2_score
This block imports the necessary libraries for data manipulation, plotting, and machine learning.
2. Generate Sample Data
np.random.seed(42) # For reproducibility X = np.linspace(0, 10, 100).reshape(-1, 1) y = 3 * X.ravel() + np.sin(2 * X.ravel()) * 5 + np.random.normal(0, 1, 100)
This block generates sample data representing a relationship with some noise, simulating real-world data variations.
3. Split the Dataset
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
This block splits the dataset into training and testing sets for model evaluation.
4. Create Polynomial Features
degree = 3 # Change this value for different polynomial degrees poly = PolynomialFeatures(degree=degree) X_poly_train = poly.fit_transform(X_train) X_poly_test = poly.transform(X_test)
This block generates polynomial features from the training and testing datasets, allowing the model to capture non-linear relationships.
5. Create and Train the k-NN Regression Model
k = 5 # Number of neighbors knn_model = KNeighborsRegressor(n_neighbors=k) knn_model.fit(X_poly_train, y_train)
This block initializes the k-NN regression model and trains it using the polynomial features derived from the training dataset.
6. Make Predictions
y_pred = knn_model.predict(X_poly_test)
This block uses the trained model to make predictions on the test set.
7. Plot the Results
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', alpha=0.5, label='Data Points')
X_grid = np.linspace(0, 10, 1000).reshape(-1, 1)
X_poly_grid = poly.transform(X_grid)
y_grid = knn_model.predict(X_poly_grid)
plt.plot(X_grid, y_grid, color='red', linewidth=2, label=f'k-NN Regression (k={k}, Degree {degree})')
plt.title(f'k-NN Regression (Polynomial Degree {degree})')
plt.xlabel('X')
plt.ylabel('Y')
plt.legend()
plt.grid(True)
plt.show()
This block creates a scatter plot of the actual data points versus the predicted values from the k-NN regression model, visualizing the fitted curve.
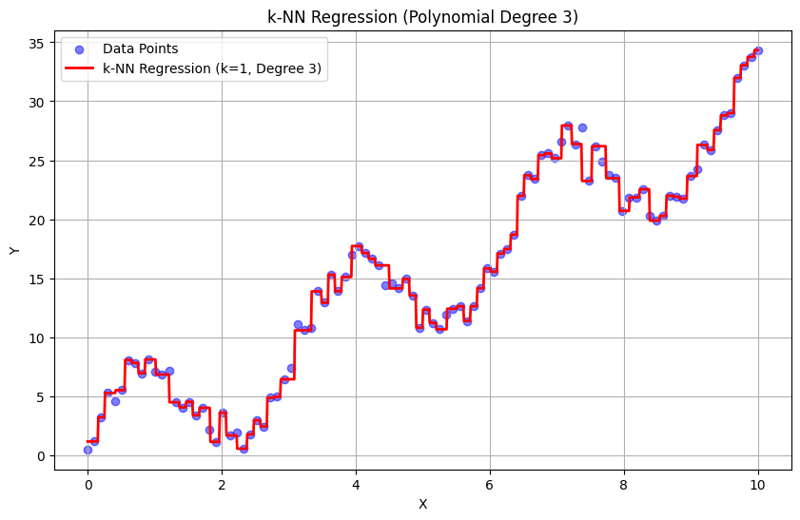
Output with k = 1:
Output with k = 10:
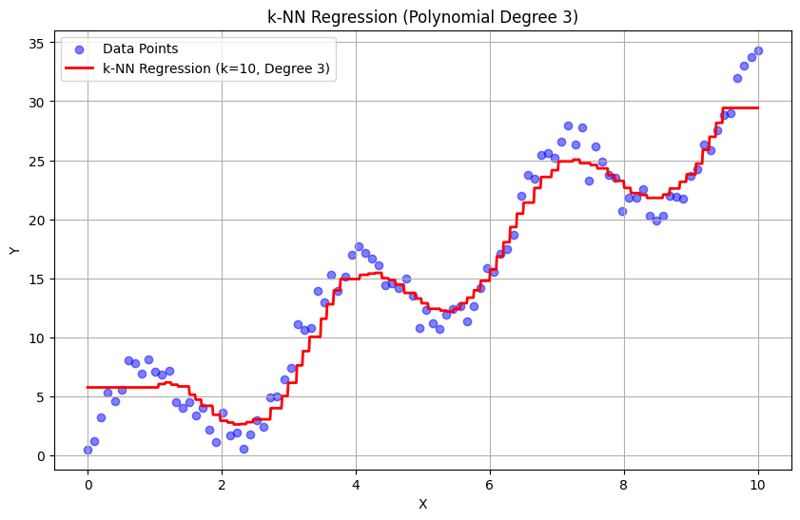
This structured approach demonstrates how to implement and evaluate k-Nearest Neighbors regression with polynomial features. By capturing local patterns through averaging the responses of nearby neighbors, k-NN regression effectively models complex relationships in data while providing a straightforward implementation. The choice of k and polynomial degree significantly influences the model's performance and flexibility in capturing underlying trends.
The above is the detailed content of K Nearest Neighbors Regression, Regression: Supervised Machine Learning. For more information, please follow other related articles on the PHP Chinese website!

