 Technology peripherals
Technology peripherals AI
AI After one day of training on a single GPU, Transformer can achieve 99% accuracy in adding 100-digit numbers.
After one day of training on a single GPU, Transformer can achieve 99% accuracy in adding 100-digit numbers.After one day of training on a single GPU, Transformer can achieve 99% accuracy in adding 100-digit numbers.
Multiplication and sorting also work.
Since it was proposed in 2017, Transformer has become the mainstream architecture for large AI models and has been firmly in the C position.
However, what all researchers have to admit is that the Transformer performs extremely poorly on arithmetic tasks, albeit addition. This flaw largely stems from the Transformer's inability to track each of the large ranges of numbers. the exact location of the number.
In order to solve this problem, researchers from the University of Maryland, CMU and other institutions have launched a challenge to this problem. They solved this problem by adding an embedding to each number that encodes the position of the number relative to the beginning. The study found that it took just one day to train 20-digit numbers on a single GPU to achieve state-of-the-art performance, with up to 99% accuracy on the 100-digit addition problem.

Paper address: https://arxiv.org/pdf/2405.17399
Project address: https://github.com/mcleish7/arithmetic
Title: Transformers Can Do Arithmetic with the Right Embeddings
Specifically, the researchers suggested that a simple modification to the data table display could resolve this shortcoming. They proposed Abacus embeddings to encode the position within the range of each digital symbol token. Using Abacus embeddings in conjunction with standard positional embeddings, the study observed significant improvements in Transformer accuracy on arithmetic tasks, such that models trained with only up to 20-digit operands scaled to problems with 120-digit operands. . This number represents a 6x SOTA scaling factor, compared to the previous state-of-the-art scaling factor of only 2.5x. It is understood that this is the longest sequence of learning addition demonstrated to date.
In addition to studying optimizing the performance of Transformer in arithmetic and generalization, this article also explores several other methods to improve the performance of Transformer. They found that they could reduce the generalization error by 50% over the Abacus embedding baseline by inserting skip connections between the input injection layer and each decoder layer. The paper also finds that the looped Transformer architecture used in conjunction with embeddings can achieve almost perfect generalization on the addition problem.
The contributions of this paper can be summarized as follows:
This paper proposes a new positional embedding, called Abacus embedding, to better capture the importance of each number properties, thereby achieving near-perfect in-distribution generalization;
Study shows that when Abacus embedding is combined with input injection and looped transformer, the performance will be further improved, and the out-of-distribution accuracy From 92.9% to 99.1%, the error is reduced by 87% compared to embeddings using the standard architecture alone;
The researchers extended these findings to more complex problems, including multiplication and sorting, also exhibiting length generalization in these domains.
Achieve length generalization of addition
The authors studied a series of methods aimed at improving the arithmetic ability of language models trained from scratch. Performance. They mainly focus on two hypotheses: 1) the position information of individual digits within a number is being lost; 2) looping can improve the reasoning ability of the Transformer architecture on multi-step arithmetic reasoning problems. The authors briefly discuss the training and evaluation settings before describing each improvement in detail.
Experimental setup
The authors trained a causal language model containing only the decoder to solve the addition problem.
They considered two standard transformer architectures. First, they use a standard autoregressive transformer model with multiple decoder layers stacked in a feed-forward fashion. Second, they augment this standard transformer model with input injection, which adds embeddings to the input of each decoder layer. The authors visually depict these architectures in Figure 20.
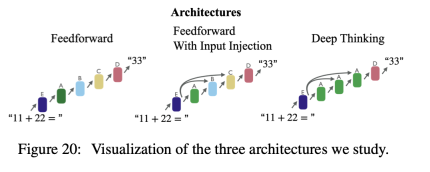
Abacus embedding helps align numbers
Through previous research and preliminary experiments, the author found that even if the entered number is displayed first Least of all numbers, the training data is hierarchical and rich (millions of examples), and it is difficult for standard transformers to learn multi-digit addition. They also observed that when humans perform long addition operations, they first arrange numbers with the same digit into columns. Therefore, the author's first hypothesis is that the digits of each number are not easily represented by the transformer, and that this subproblem poses a greater obstacle than the actual addition itself.
To address the limitations of the transformer in representing positional information, the authors designed a special positional embedding that encodes the position of each number relative to the starting position of the current number. The authors call this Abacus embedding. They apply the same positional embedding to all numbers with the same digit, providing an explicit signal that the model can use to align the numbers, as shown in Figure 2.

Abacus embedding solves the addition problem
For standard transformer architectures, Abacus embedding improves generalization performance to 100 bits and beyond. In Figure 3 (left), the authors highlight the comparative advantage of Abacus embeddings over standard transformer architectures and embeddings when performing additive operations, taking the average accuracy across all cases across the three models.
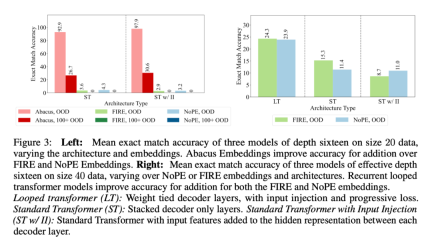
Figure 1 also shows accuracy results for standard transformer models trained with FIRE and Abacus, which were tested both in-domain (ID) and out-of-domain (OOD). 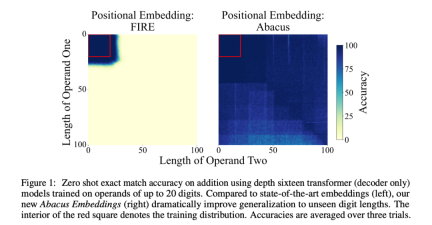
Loops in Transformer improve performance
After solving the position embedding problem, the author next explored whether the loop architecture can further improve the transformer execution of multiple bits Ability to add numbers. They use the term "recurrent block" to refer to a set of decoder layers with different weights, and "recurrence" refers to the number of repetitions of the recurrent block. The authors use the term effective depth to refer to the number of layers used in a transformer, regardless of whether their weights are unique. Unless otherwise stated, they use a max-loop architecture, which only loops through a unique layer to reach effective depth. They also used input injection and residual connections to propagate a copy of the input to each layer in the network.
Advantages of Loops
In Figure 3 (right), the authors compare all training methods using FIRE and NoPE embeddings for additions with operands up to 40 bits. Architecture variants. Although the number of parameters is only 1/10 of the other models, we can see that the looped transformer (looped, with input injection and progressive loss) achieves the best out-of-distribution performance when using any kind of positional embedding. In Figure 8, the authors demonstrate the robustness of this result across a variety of training data sizes.

For recurrent models, you can choose to change the number of loops for each forward pass during training. This tends to improve the generalization ability of the model to more difficult tasks when testing, which is also called progressive loss computation. This loss function is a convex combination of the loss values of two forward passes, one using a literal number of cycles (16 for the 1 × 16 model) and the other using a randomly smaller number of cycles.
Next, the authors explore the effect of changing the loop block size while keeping the effective depth fixed. They halved the number of layers in the loop block and doubled the loop count, going from a model with 16 layers in the block and only one loop count (16 × 1, the standard transformer) to a model with only one layer in the block and loop count There are 16 times (1 × 16) models.
Analyzing these results through Figure 4, the authors found that in some cases combining loops and Abacus embeddings can further improve performance. Specifically, on the OOD problem, the model with two cycles (8 × 2) produced half the error of the purely acyclic model (16 × 1), while on the OOD problem with 100+, its accuracy was also slightly higher. improve.
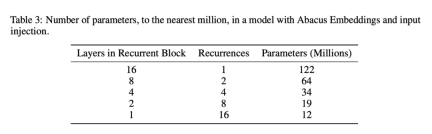
Finally, in Appendix A.7.3, the authors vary the effective depth of the model to analyze the impact of the number of parameters on this task, including Abacus, FIRE, and NoPE embeddings. While the experiments in Figure 4 are a fair comparison of different depths, the pure standard transformer model has many more parameters than the corresponding loop model. In Table 3 in the Appendix, the authors record parameter quantities to the nearest million.

Experiment
The researchers not only discussed addition problems, but also multiplication problems and sorting were studied.
Integer multiplication
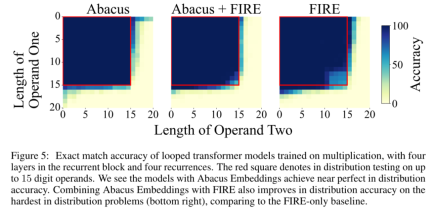
Figure 5 shows that the Abacus embedding model exceeds previous work in the distribution of 15-digit multiplications without requiring zeros for each digit. operands are padded to the same length. In particular, the study highlights that combining Abacus embeddings with FIRE also improves accuracy on the hardest distribution problems (bottom right) compared to the baseline using FIRE alone.
Array sort
Table 1 shows the performance of a standard transformer (eight layers) trained with different embeddings—FIRE, Abacus, and their combinations. The results show that the combined embedding method enhances the generalization ability of the model.

As shown in Table 2, the researchers observed that when pairing the Abacus+FIRE embedding combination with different model architectures (effective depth of 8), the results showed mixed sex.

Abacus and related embeddings
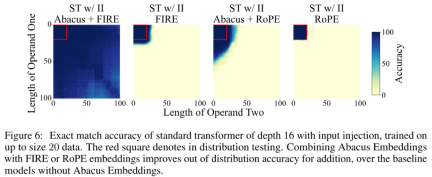
Figure 6 illustrates the real potential of integrating Abacus embeddings into more general systems, showing Abacus embedding combined with FIRE unlocks problem-solving capabilities that go far beyond FIRE embedding.
For more research details, please refer to the original paper.
The above is the detailed content of After one day of training on a single GPU, Transformer can achieve 99% accuracy in adding 100-digit numbers.. For more information, please follow other related articles on the PHP Chinese website!
 Why Sam Altman And Others Are Now Using Vibes As A New Gauge For The Latest Progress In AIMay 06, 2025 am 11:12 AM
Why Sam Altman And Others Are Now Using Vibes As A New Gauge For The Latest Progress In AIMay 06, 2025 am 11:12 AMLet's discuss the rising use of "vibes" as an evaluation metric in the AI field. This analysis is part of my ongoing Forbes column on AI advancements, exploring complex aspects of AI development (see link here). Vibes in AI Assessment Tradi
 Inside The Waymo Factory Building A Robotaxi FutureMay 06, 2025 am 11:11 AM
Inside The Waymo Factory Building A Robotaxi FutureMay 06, 2025 am 11:11 AMWaymo's Arizona Factory: Mass-Producing Self-Driving Jaguars and Beyond Located near Phoenix, Arizona, Waymo operates a state-of-the-art facility producing its fleet of autonomous Jaguar I-PACE electric SUVs. This 239,000-square-foot factory, opened
 Inside S&P Global's Data-Driven Transformation With AI At The CoreMay 06, 2025 am 11:10 AM
Inside S&P Global's Data-Driven Transformation With AI At The CoreMay 06, 2025 am 11:10 AMS&P Global's Chief Digital Solutions Officer, Jigar Kocherlakota, discusses the company's AI journey, strategic acquisitions, and future-focused digital transformation. A Transformative Leadership Role and a Future-Ready Team Kocherlakota's role
 The Rise Of Super-Apps: 4 Steps To Flourish In A Digital EcosystemMay 06, 2025 am 11:09 AM
The Rise Of Super-Apps: 4 Steps To Flourish In A Digital EcosystemMay 06, 2025 am 11:09 AMFrom Apps to Ecosystems: Navigating the Digital Landscape The digital revolution extends far beyond social media and AI. We're witnessing the rise of "everything apps"—comprehensive digital ecosystems integrating all aspects of life. Sam A
 Mastercard And Visa Unleash AI Agents To Shop For YouMay 06, 2025 am 11:08 AM
Mastercard And Visa Unleash AI Agents To Shop For YouMay 06, 2025 am 11:08 AMMastercard's Agent Pay: AI-Powered Payments Revolutionize Commerce While Visa's AI-powered transaction capabilities made headlines, Mastercard has unveiled Agent Pay, a more advanced AI-native payment system built on tokenization, trust, and agentic
 Backing The Bold: Future Ventures' Transformative Innovation PlaybookMay 06, 2025 am 11:07 AM
Backing The Bold: Future Ventures' Transformative Innovation PlaybookMay 06, 2025 am 11:07 AMFuture Ventures Fund IV: A $200M Bet on Novel Technologies Future Ventures recently closed its oversubscribed Fund IV, totaling $200 million. This new fund, managed by Steve Jurvetson, Maryanna Saenko, and Nico Enriquez, represents a significant inv
 As AI Use Soars, Companies Shift From SEO To GEOMay 05, 2025 am 11:09 AM
As AI Use Soars, Companies Shift From SEO To GEOMay 05, 2025 am 11:09 AMWith the explosion of AI applications, enterprises are shifting from traditional search engine optimization (SEO) to generative engine optimization (GEO). Google is leading the shift. Its "AI Overview" feature has served over a billion users, providing full answers before users click on the link. [^2] Other participants are also rapidly rising. ChatGPT, Microsoft Copilot and Perplexity are creating a new “answer engine” category that completely bypasses traditional search results. If your business doesn't show up in these AI-generated answers, potential customers may never find you—even if you rank high in traditional search results. From SEO to GEO – What exactly does this mean? For decades
 Big Bets On Which Of These Pathways Will Push Today's AI To Become Prized AGIMay 05, 2025 am 11:08 AM
Big Bets On Which Of These Pathways Will Push Today's AI To Become Prized AGIMay 05, 2025 am 11:08 AMLet's explore the potential paths to Artificial General Intelligence (AGI). This analysis is part of my ongoing Forbes column on AI advancements, delving into the complexities of achieving AGI and Artificial Superintelligence (ASI). (See related art


Hot AI Tools

Undresser.AI Undress
AI-powered app for creating realistic nude photos

AI Clothes Remover
Online AI tool for removing clothes from photos.

Undress AI Tool
Undress images for free

Clothoff.io
AI clothes remover

Video Face Swap
Swap faces in any video effortlessly with our completely free AI face swap tool!

Hot Article

Hot Tools

WebStorm Mac version
Useful JavaScript development tools

Safe Exam Browser
Safe Exam Browser is a secure browser environment for taking online exams securely. This software turns any computer into a secure workstation. It controls access to any utility and prevents students from using unauthorized resources.

VSCode Windows 64-bit Download
A free and powerful IDE editor launched by Microsoft

Dreamweaver CS6
Visual web development tools

DVWA
Damn Vulnerable Web App (DVWA) is a PHP/MySQL web application that is very vulnerable. Its main goals are to be an aid for security professionals to test their skills and tools in a legal environment, to help web developers better understand the process of securing web applications, and to help teachers/students teach/learn in a classroom environment Web application security. The goal of DVWA is to practice some of the most common web vulnerabilities through a simple and straightforward interface, with varying degrees of difficulty. Please note that this software





