Heim >Web-Frontend >js-Tutorial >Detaillierte Erläuterung der JavaScript-Datenstruktur und der Algorithmus-Stack_Javascript-Fähigkeiten
Detaillierte Erläuterung der JavaScript-Datenstruktur und der Algorithmus-Stack_Javascript-Fähigkeiten
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2016-05-16 16:10:141240Durchsuche
Im vorherigen Artikel hat der Blog die folgende Liste vorgestellt. Die Liste ist die einfachste Struktur, aber wenn Sie sich mit einigen komplexeren Strukturen befassen möchten, ist die Liste zu einfach, also brauchen wir etwas of und Lists ähneln, aber komplexeren Datenstrukturen – Stacks. Der Stapel ist eine effiziente Datenstruktur, da Daten nur oben im Stapel hinzugefügt oder gelöscht werden können, sodass dieser Vorgang schnell und einfach zu implementieren ist.
1: Operationen auf dem Stapel.
Der Stapel ist eine besondere Art von Liste. Auf die Elemente im Stapel kann nur über ein Ende der Liste zugegriffen werden, das sich am oberen Ende des Stapels befindet. Wenn Sie beispielsweise in einem Restaurant Geschirr spülen, können Sie zuerst nur den oberen Teller abwaschen. Nachdem der Teller abgewaschen ist, kann er nur noch oben auf den Tellerstapel geschraubt werden. Der Stapel ist eine Datenstruktur namens „Last In, First Out“ (LIFO).
Da der Stapel die Last-In-First-Out-Eigenschaft hat, kann nicht auf jedes Element zugegriffen werden, das sich nicht oben im Stapel befindet. Um das Element unten im Stapel zu erhalten, muss es sein zuerst entfernt. Die beiden Hauptoperationen, die wir am Stapel ausführen können, sind das Schieben eines Elements auf den Stapel und das Entfernen eines Elements vom Stapel. Wir können die Methode push() verwenden, um in den Stapel zu schieben, und die Methode pop(), um aus dem Stapel herauszuspringen. Obwohl die Methode pop() auf das Element oben im Stapel zugreifen kann, wird das Element oben im Stapel nach dem Aufruf dieser Methode dauerhaft aus dem Stapel gelöscht. Eine weitere häufig verwendete Methode ist peek(), die nur das oberste Element des Stapels zurückgibt, ohne es zu löschen.
Das eigentliche Diagramm zum Schieben und Platzieren auf den Stapel sieht wie folgt aus:
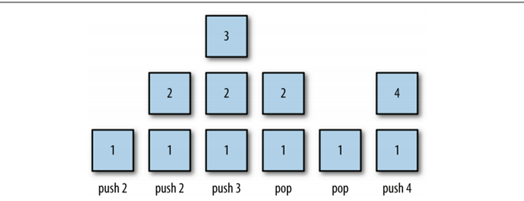
push(), pop() und peek() sind die drei Hauptmethoden des Stapels, aber der Stapel verfügt über andere Methoden und Eigenschaften. Wie folgt:
clear(): Alle Elemente im Stapel löschen.
length(): Zeichnen Sie die Anzahl der Elemente im Stapel auf.
2: Die Implementierung des Stapels ist wie folgt:
Wir können damit beginnen, die Methoden der Stack-Klasse wie folgt zu implementieren:
Funktion Stack() {
This.dataStore = [];
This.top = 0;
}
Wie oben: dataStore speichert alle Elemente im Stapel. Die Variable top zeichnet die Position der Oberseite des Stapels auf und wird auf 0 initialisiert. Dies bedeutet, dass die Startposition des Arrays, die der Oberseite des Stapels entspricht, 0 ist, wenn ein Element auf den Stapel geschoben wird. Der Variablenwert ändert sich entsprechend.
Wir haben auch die folgenden Methoden: push(), pop(), peek(), clear(), length();
1. Push()-Methode: Wenn ein neues Element in den Stapel verschoben wird, muss es an der Position gespeichert werden, die der Variablen oben im Array entspricht, und dann wird der oberste Wert um 1 erhöht, um auf das nächste zu zeigen Position im Array. Der folgende Code:
Funktion push(element) {
This.dataStore[this.top] = element;
}
2. Die Methode pop() ist das Gegenteil der Methode push() – sie gibt das oberste Element des Stapels zurück und dekrementiert den obersten Wert um 1. Der folgende Code:
Funktion pop(){
return this.dataStore[--this.top];
}
3. Die peek()-Methode gibt das Element an der obersten Position des Arrays zurück, das das oberste Element des Stapels ist;
return this.dataStore[this.top - 1];
}
return this.top;
}
Funktion clear() {
this.top = 0;
}
Alle Codes unten:
Funktion Stack() {
This.dataStore = [];
This.top = 0;
}
Stack.prototype = {
//Schiebe ein neues Element in den Stapel
Push: Funktion(Element) {
This.dataStore[this.top] = element;
},
// Auf das oberste Element des Stapels zugreifen, das oberste Element des Stapels wird dauerhaft gelöscht
pop: function(){
return this.dataStore[--this.top];
},
// Das Element an der obersten 1-Position im Array zurückgeben, d. h. das oberste Element des Stapels
peek: function(){
return this.dataStore[this.top - 1];
},
//Wie viele Elemente werden im Stapel gespeichert
Länge: function(){
return this.top;
},
//Stapel leeren
; klar: function(){
This.top = 0;
}
};
Das Demo-Beispiel sieht wie folgt aus:
var stack = new Stack();
stack.push("a");
stack.push("b");
stack.push("c");
console.log(stack.length()); // 3
console.log(stack.peek()); // c
var popped = stack.pop();
console.log(popped); // c
console.log(stack.peek()); // b
stack.push("d");
console.log(stack.peek()); // d
stack.clear();
console.log(stack.length()); // 0
console.log(stack.peek()); // undefiniert
Nachfolgend können wir eine rekursive Definition der Fakultätsfunktion implementieren, z. B. 5! Die Fakultät von 5! = 5 * 4 * 3 * 2 * 1;
Der folgende Code:
var s = new Stack();
; while(n > 1) {
s.push(n--);
}
var Produkt = 1;
While(s.length() > 0) {
Produkt *= s.pop();
}
Produkt zurückgeben;
}
console.log(fact(5));
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

