Heim >Technologie-Peripheriegeräte >KI >MLP wurde über Nacht getötet! MIT Caltech und andere revolutionäre KANs brechen Rekorde und entdecken mathematische Theoreme, die DeepMind zerstören
MLP wurde über Nacht getötet! MIT Caltech und andere revolutionäre KANs brechen Rekorde und entdecken mathematische Theoreme, die DeepMind zerstören
- PHPznach vorne
- 2024-05-06 15:10:011096Durchsuche
Über Nacht wird sich das Paradigma des maschinellen Lernens ändern!
Heutzutage ist die Infrastruktur, die den Bereich des Deep Learning dominiert, das Multilayer Perceptron (MLP), das Aktivierungsfunktionen auf Neuronen platziert.
Gibt es darüber hinaus einen neuen Weg, den wir einschlagen können?


Erst heute haben Teams vom MIT, dem California Institute of Technology, der Northeastern University und anderen Institutionen eine neue neuronale Netzwerkstruktur veröffentlicht – Kolmogorov-Arnold Networks (KAN).

Die Forscher haben eine einfache Änderung am MLP vorgenommen, nämlich die lernbare Aktivierungsfunktion von den Knoten (Neuronen) zu den Kanten (Gewichten) zu verschieben!

Papieradresse: https://arxiv.org/pdf/2404.19756
Diese Änderung mag zunächst unbegründet erscheinen, hat aber etwas mit „Approximationstheorien“ in der Mathematik zu tun. Ziemlich tiefe Verbindung.
Es stellt sich heraus, dass die Kolmogorov-Arnold-Darstellung einem zweischichtigen Netzwerk entspricht, mit lernbaren Aktivierungsfunktionen an den Kanten, nicht an den Knoten.
Inspiriert vom Darstellungssatz verwendeten Forscher neuronale Netze, um die Kolmogorov-Arnold-Darstellung explizit zu parametrisieren.
Es ist erwähnenswert, dass der Ursprung des Namens KAN im Gedenken an die beiden großen verstorbenen Mathematiker Andrey Kolmogorov und Vladimir Arnold liegt.

Experimentelle Ergebnisse zeigen, dass KAN eine bessere Leistung als herkömmliches MLP aufweist und die Genauigkeit und Interpretierbarkeit neuronaler Netze verbessert.

Das Unerwartetste ist, dass die Visualisierung und Interaktivität von KAN ihm potenziellen Anwendungswert in der wissenschaftlichen Forschung verleiht und Wissenschaftlern dabei helfen kann, neue mathematische und physikalische Gesetze zu entdecken.
In der Recherche nutzte der Autor KAN, um die mathematischen Gesetze in der Knotentheorie wiederzuentdecken!
Darüber hinaus hat KAN die Ergebnisse von DeepMind im Jahr 2021 mit einem kleineren Netzwerk und Automatisierung wiederholt.

In der Physik kann KAN Physikern dabei helfen, die Anderson-Lokalisierung (einen Phasenübergang in der Physik der kondensierten Materie) zu untersuchen.
Übrigens können alle KAN-Beispiele in der Studie (außer Parameter-Scanning) in weniger als 10 Minuten auf einer einzelnen CPU reproduziert werden.

Die Entstehung von KAN stellte eine direkte Herausforderung für die MLP-Architektur dar, die den Bereich des maschinellen Lernens schon immer dominiert hatte, und löste im gesamten Netzwerk Aufruhr aus.
Eine neue Ära des maschinellen Lernens hat begonnen
Manche Leute sagen, dass eine neue Ära des maschinellen Lernens begonnen hat!

Google DeepMind-Forscher sagte: „Kolmogorov-Arnold schlägt erneut zu! Eine wenig bekannte Tatsache: Dieses Theorem erschien in einer wegweisenden Arbeit über permutationsinvariante neuronale Netze (Tiefenmengen) und zeigte, dass diese Darstellung einen komplexen Zusammenhang mit der Art und Weise zeigt, wie Ensembles/ GNN-Aggregatoren werden gebaut (als Sonderfall)“.

Eine brandneue neuronale Netzwerkarchitektur war geboren! KAN wird die Art und Weise, wie künstliche Intelligenz trainiert und verfeinert wird, dramatisch verändern.


Ist die KI in die 2.0-Ära eingetreten?

Einige Internetnutzer verwendeten eine populäre Sprache, um eine anschauliche Metapher für den Unterschied zwischen KAN und MLP zu finden:
Das Kolmogorov-Arnold-Netzwerk (KAN) ist wie ein dreidimensionales Netzwerk, das jeden Kuchen backen kann . Ein Schichtkuchenrezept, während ein Multi-Layer Perceptron (MLP) ein individueller Kuchen mit unterschiedlicher Anzahl von Schichten ist. MLP ist komplexer, aber allgemeiner, während KAN statisch, aber einfacher und schneller für eine Aufgabe ist.

Der Autor des Papiers, MIT-Professor Max Tegmark, sagte, dass das neueste Papier zeigt, dass eine völlig andere Architektur als das standardmäßige neuronale Netzwerk bei der Bearbeitung interessanter physikalischer und mathematischer Probleme bessere Ergebnisse mit weniger Parametern erzielen kann . Hohe Präzision.

Als nächstes werfen wir einen Blick darauf, wie KAN, das die Zukunft des Deep Learning darstellt, implementiert wird?
KAN zurück am Pokertisch
Theoretische Basis von KAN
Der Kolmogorov-Arnold-Darstellungssatz (Kolmogorov-Arnold-Darstellungssatz) besagt, dass, wenn f auf einem begrenzten Gebiet definiert ist, eine kontinuierliche Funktion mit mehreren Variablen dann kann die Funktion als endliche Kombination mehrerer einvariabler, additiver stetiger Funktionen ausgedrückt werden.

Für maschinelles Lernen kann das Problem wie folgt beschrieben werden: Der Prozess des Lernens einer hochdimensionalen Funktion kann vereinfacht werden, um eine eindimensionale Funktion einer Polynomgröße zu lernen.
Aber diese eindimensionalen Funktionen können nicht glatt oder sogar fraktal sein und in der Praxis möglicherweise nicht erlernt werden. Genau wegen dieses „pathologischen Verhaltens“ wurde der Kolmogorov-Arnold-Darstellungssatz auf dem Gebiet der Maschine verwendet Beim Lernen wird es im Grunde zum „Tod“ verurteilt, das heißt, die Theorie ist richtig, aber in der Praxis nutzlos.
In diesem Artikel sind die Forscher immer noch optimistisch, was die Anwendung dieses Theorems im Bereich des maschinellen Lernens angeht, und schlagen zwei Verbesserungen vor:
1 In der ursprünglichen Gleichung gibt es nur zwei Ebenen der Nichtlinearität und eine verborgene Schicht (2n+1), die das Netzwerk auf beliebige Breite und Tiefe verallgemeinern kann
2 Die meisten Funktionen in der Wissenschaft und im täglichen Leben sind größtenteils glatt und weisen spärliche kombinatorische Strukturen auf, die dazu beitragen können, eine glatte Kolmogorov-Struktur zu bilden. Arnold-Darstellung. Ähnlich wie beim Unterschied zwischen Physikern und Mathematikern befassen sich Physiker eher mit typischen Szenarien, während Mathematiker sich eher mit Worst-Case-Szenarien befassen.
KAN-Architektur
Die Kernidee des Entwurfs des Kolmogorov-Arnold-Netzwerks (KAN) besteht darin, das Approximationsproblem von Funktionen mit mehreren Variablen in das Problem des Lernens einer Reihe von Funktionen mit einer Variablen umzuwandeln. Innerhalb dieses Rahmens kann jede univariate Funktion mit einem B-Spline parametrisiert werden, einer lokalen, stückweisen Polynomkurve, deren Koeffizienten lernbar sind.

Um das zweischichtige Netzwerk im ursprünglichen Satz tiefer und weiter zu erweitern, schlugen die Forscher eine „verallgemeinerte“ Version des Satzes vor, um das Design von KAN zu unterstützen:
Beeinflusst durch die Stapelstruktur von MLPs Inspiriert durch die Verbesserung der Netzwerktiefe stellt der Artikel auch ein ähnliches Konzept vor, die KAN-Schicht, die aus einer eindimensionalen Funktionsmatrix besteht und jede Funktion über trainierbare Parameter verfügt.

Nach dem Kolmogorov-Arnold-Theorem besteht die ursprüngliche KAN-Schicht aus internen Funktionen und externen Funktionen, die jeweils unterschiedlichen Eingabe- und Ausgabedimensionen entsprechen. Diese Entwurfsmethode zum Stapeln von KAN-Schichten erweitert nicht nur die Tiefe von KANs und erhält die Interpretierbarkeit und Ausdruckskraft des Netzwerks. Jede Schicht besteht aus Funktionen mit einer Variablen, und die Funktionen können unabhängig voneinander gelernt und verstanden werden.
f in der folgenden Formel entspricht KAN

Implementierungsdetails
Obwohl das Designkonzept von KAN einfach zu sein scheint und ausschließlich auf Stapeln basiert, ist es nicht einfach zu optimieren, was auch für Forscher gilt lernte während des Trainingsprozesses einige Techniken.
1. Restaktivierungsfunktion: Durch die Einführung einer Kombination aus Basisfunktion b(x) und Spline-Funktion und die Verwendung des Konzepts der Restverbindung zur Konstruktion der Aktivierungsfunktion ϕ(x) trägt es zur Stabilität des Trainings bei Verfahren.

2. Initialisierungsskalen (Skalen): Die Initialisierung der Aktivierungsfunktion wird auf eine Spline-Funktion nahe Null eingestellt, und das Gewicht w verwendet die Xavier-Initialisierungsmethode, die dazu beiträgt, die Stabilität des Gradienten aufrechtzuerhalten in der Anfangsphase der Ausbildung.
3. Aktualisieren Sie das Spline-Gitter: Da die Spline-Funktion innerhalb eines begrenzten Intervalls definiert ist und der Aktivierungswert dieses Intervall während des Trainingsprozesses des neuronalen Netzwerks überschreiten kann, kann die dynamische Aktualisierung des Spline-Gitters sicherstellen, dass die Spline-Funktion immer funktioniert im entsprechenden Bereich liegen.
Parameter: 1. Netzwerktiefe: L: 2. Breite jeder Ebene: N k-Reihenfolge (normalerweise k=3)
Die Parametermenge von KANs beträgt also ungefähr
Zum Vergleich: Die Parametermenge von MLP ist O(L*N^2), was besser zu sein scheint als KAN ist effizienter, aber KANs können kleinere Schichtbreiten (N) verwenden, was nicht nur die Generalisierungsleistung, sondern auch die Interpretierbarkeit verbessert.
Inwiefern ist KAN besser als MLP?
Stärkere Leistung
Verwendung von MLPs mit unterschiedlichen Tiefen und Breiten als Basismodelle, und sowohl KANs als auch MLPs verwenden den LBFGS-Algorithmus. Insgesamt waren 1800 Schritte erforderlich trainiert, und RMSE wurde als Vergleichsindikator verwendet.
Wie Sie den Ergebnissen entnehmen können, ist die KAN-Kurve nervöser, kann schnell konvergieren und erreicht einen stabilen Zustand und ist besser als die Skalierungskurve von MLP, insbesondere in hochdimensionalen Situationen.
Es ist auch ersichtlich, dass die Leistung von dreischichtigem KAN viel stärker ist als die von zweischichtigem, was darauf hindeutet, dass tiefere KANs erwartungsgemäß stärkere Ausdrucksfähigkeiten haben.
Interaktive Erklärung von KAN
Die Forscher haben ein einfaches Regressionsexperiment entworfen, um zu zeigen, dass Benutzer während der Interaktion mit KAN die am besten interpretierbaren Ergebnisse erzielen können.

Unter der Annahme, dass der Benutzer daran interessiert ist, die symbolische Formel herauszufinden, gibt es insgesamt 5 interaktive Schritte.

Schritt 1: Training mit Sparsifikation.
Ausgehend von einem vollständig verbundenen KAN kann das Training mit spärlicher Regularisierung das Netzwerk spärlicher machen, sodass festgestellt werden kann, dass 4 der 5 Neuronen in der verborgenen Schicht keine Wirkung zu haben scheinen.
Schritt 2: Beschneiden
Nach dem automatischen Beschneiden alle nutzlosen versteckten Neuronen verwerfen, sodass nur ein KAN übrig bleibt, und die Aktivierungsfunktion an die bekannte Vorzeichenfunktion anpassen. 🔜 oder nicht weiß, welche symbolischen Funktionen die Aktivierungsfunktion haben kann, stellen die Forscher eine Funktion suggest_symbolic bereit, um symbolische Kandidaten vorzuschlagen.
Schritt 4: Weiteres Training
Nachdem alle Aktivierungsfunktionen im Netzwerk symbolisiert sind, sind die einzigen verbleibenden Parameter die affinen Parameter. Fahren Sie mit dem Training der affinen Parameter fort, wenn Sie sehen, dass der Verlust auf Maschinengenauigkeit (Maschinenpräzision) sinkt. , erkennen Sie, dass das Modell den richtigen symbolischen Ausdruck gefunden hat.
 Schritt 5: Symbolische Formel ausgeben
Schritt 5: Symbolische Formel ausgeben
Verwenden Sie Sympy, um die symbolische Formel des Ausgabeknotens zu berechnen und die richtige Antwort zu überprüfen.
Überprüfung der Interpretierbarkeit
Die Forscher entwarfen zunächst sechs Proben in einem überwachten Spielzeugdatensatz, um die kombinatorischen Strukturfähigkeiten des KAN-Netzwerks anhand symbolischer Formeln zu demonstrieren.
Es ist ersichtlich, dass KAN die korrekte Einzelvariablenfunktion erfolgreich gelernt hat und durch Visualisierung den Denkprozess von KAN erklären kann.
In einer unbeaufsichtigten Umgebung enthält der Datensatz nur das Eingabemerkmal x. Durch die Gestaltung der Verbindung zwischen bestimmten Variablen (x1, x2, x3) kann die Fähigkeit des KAN-Modells getestet werden, Abhängigkeiten zwischen Variablen zu finden.
Den Ergebnissen zufolge hat das KAN-Modell die funktionale Abhängigkeit zwischen Variablen erfolgreich gefunden, der Autor wies jedoch auch darauf hin, dass Experimente immer noch nur mit synthetischen Daten durchgeführt werden und eine systematischere und kontrollierbarere Methode erforderlich ist vollständige Zusammenhänge zu entdecken. 
Pareto Optimal
Durch die Anpassung spezieller Funktionen zeigen die Autoren die Pareto-Grenze von KAN und MLP in der Ebene, die durch die Anzahl der Modellparameter und den RMSE-Verlust aufgespannt wird. 
Unter allen Sonderfunktionen hat KAN immer eine bessere Pareto-Front als MLP.

Partielle Differentialgleichungen lösen
Bei der Lösung partieller Differentialgleichungen zeichneten die Forscher die L2-Quadrat- und H1-Quadrat-Verluste zwischen der vorhergesagten und der wahren Lösung auf.
In der folgenden Abbildung sind die ersten beiden die Trainingsdynamik des Verlusts und die dritte und vierte das Sacling-Gesetz der Anzahl der Verlustfunktionen.
Wie in den folgenden Ergebnissen gezeigt wird, konvergiert KAN schneller, weist geringere Verluste auf und weist im Vergleich zu MLP ein steileres Expansionsgesetz auf.

Kontinuierliches Lernen, katastrophales Vergessen wird nicht auftreten
Wir alle wissen, dass katastrophales Vergessen ein ernstes Problem beim maschinellen Lernen darstellt.
Der Unterschied zwischen künstlichen neuronalen Netzen und dem Gehirn besteht darin, dass das Gehirn über verschiedene Module verfügt, die lokal im Raum funktionieren. Beim Erlernen einer neuen Aufgabe kommt es nur in den für die jeweilige Fertigkeit zuständigen lokalen Bereichen zu einer strukturellen Neuordnung, während andere Bereiche unverändert bleiben.
Allerdings verfügen die meisten künstlichen neuronalen Netze, einschließlich MLP, nicht über dieses Konzept der Lokalität, was der Grund für katastrophales Vergessen sein kann.
Untersuchungen haben gezeigt, dass KAN über lokale Plastizität verfügt und die Splines-Lokalität nutzen kann, um katastrophales Vergessen zu vermeiden.
Die Idee ist sehr einfach: Da der Spline lokal ist, wirkt sich die Probe nur auf einige nahe gelegene Spline-Koeffizienten aus, während die entfernten Koeffizienten unverändert bleiben.
Da MLP im Gegensatz dazu normalerweise eine globale Aktivierung verwendet (wie ReLU/Tanh/SiLU), können sich lokale Änderungen unkontrolliert in entfernte Regionen ausbreiten und die dort gespeicherten Informationen zerstören.
Die Forscher haben eine eindimensionale Regressionsaufgabe (bestehend aus 5 Gaußschen Peaks) übernommen. Die Daten um jeden Peak herum werden KAN und MLP nacheinander (und nicht alle auf einmal) präsentiert.
Die Ergebnisse sind in der folgenden Abbildung dargestellt. KAN rekonstruiert nur den Bereich, in dem Daten in der aktuellen Phase vorhanden sind, und lässt den vorherigen Bereich unverändert.
Und MLP wird den gesamten Bereich umgestalten, nachdem er neue Datenproben gesehen hat, was zu katastrophalem Vergessen führt.

Entdeckte die Knotentheorie und die Ergebnisse übertrafen DeepMind
Was bedeutet die Geburt von KAN für die zukünftige Anwendung des maschinellen Lernens?
Die Knotentheorie ist eine Disziplin der niederdimensionalen Topologie. Sie deckt die topologischen Probleme von Drei- und Viermannigfaltigkeiten auf und findet breite Anwendung in Bereichen wie der Biologie und dem topologischen Quantencomputing.

Im Jahr 2021 nutzte das DeepMind-Team KI, um die Knotentheorie zum ersten Mal in der Natur zu beweisen.
... algebraische und geometrische Knoteninvarianten.
Das heißt, die Gradientensalienz identifizierte wichtige Invarianten des Überwachungsproblems, was Fachexperten dazu veranlasste, eine Vermutung aufzustellen, die anschließend verfeinert und bewiesen wurde.
In diesem Zusammenhang untersucht der Autor, ob KAN bei demselben Problem gute interpretierbare Ergebnisse erzielen kann, um die Signatur von Knoten vorherzusagen.
Im DeepMind-Experiment sind die Hauptergebnisse ihrer Untersuchung des Knotentheorie-Datensatzes:
1 Mithilfe der Netzwerkattributionsmethode wurde festgestellt, dass die Signatur 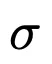 hauptsächlich vom Zwischenabstand
hauptsächlich vom Zwischenabstand  und dem Längsabstand λ abhängt.
und dem Längsabstand λ abhängt.
2 , wobei die Signatur als Ausgabe behandelt wird.  Ähnlich wie bei der Einrichtung in DeepMind werden Signaturen (gerade Zahlen) als One-Hot-Vektoren codiert und das Netzwerk wird mit Kreuzentropieverlust trainiert.
Ähnlich wie bei der Einrichtung in DeepMind werden Signaturen (gerade Zahlen) als One-Hot-Vektoren codiert und das Netzwerk wird mit Kreuzentropieverlust trainiert.  Die Ergebnisse ergaben, dass ein sehr kleines KAN eine Testgenauigkeit von 81,6 % erreichen kann, während DeepMinds 4-Schichten-Breite 300MLP nur eine Testgenauigkeit von 78 % erreichte.
Die Ergebnisse ergaben, dass ein sehr kleines KAN eine Testgenauigkeit von 81,6 % erreichen kann, während DeepMinds 4-Schichten-Breite 300MLP nur eine Testgenauigkeit von 78 % erreichte. 
Wie in der folgenden Tabelle gezeigt, hat KAN (G = 3, k = 3) etwa 200 Parameter, während MLP etwa 300.000 Parameter hat.
Es ist erwähnenswert, dass KAN nicht nur genauer ist; Gleichzeitig sind die Parameter effizienter als MLP.
Im Hinblick auf die Interpretierbarkeit skalierten die Forscher die Transparenz jeder Aktivierung anhand ihrer Größe, sodass ohne Merkmalszuordnung sofort klar war, welche Eingabevariablen wichtig waren.
Dann wird KAN auf drei wichtige Variablen trainiert und erreicht eine Testgenauigkeit von 78,2 %. 
Wie folgt, entdeckte der Autor durch KAN drei mathematische Beziehungen im Knotendatensatz wieder.
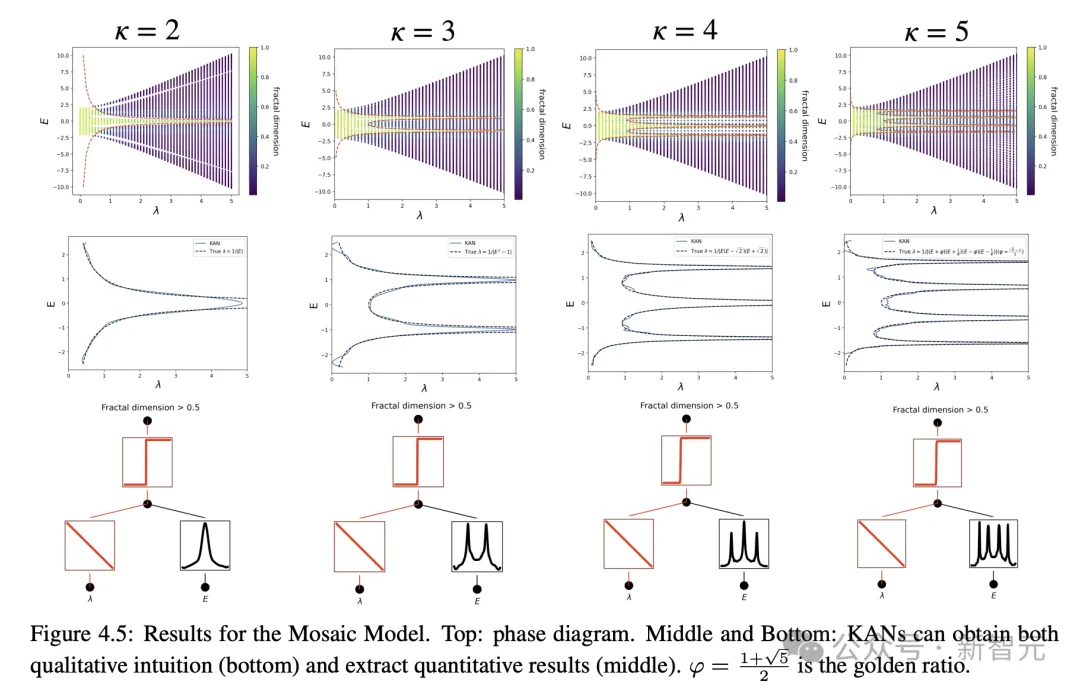
Die physikalische Anderson-Lokalisierung wurde gelöst
 Und auch in physikalischen Anwendungen hat KAN einen großen Wert gespielt.
Und auch in physikalischen Anwendungen hat KAN einen großen Wert gespielt.
Anderson ist ein grundlegendes Phänomen, bei dem eine Störung in einem Quantensystem zur Lokalisierung der Elektronenwellenfunktion führt, wodurch jegliche Übertragung zum Erliegen kommt.

Im Gegensatz dazu bildet eine kritische Energie in drei Dimensionen eine Phasengrenze, die erweiterte Zustände von lokalisierten Zuständen trennt, was als Mobilitätskante bezeichnet wird.
Das Verständnis dieser Mobilitätskanten ist entscheidend für die Erklärung verschiedener grundlegender Phänomene wie Metall-Isolator-Übergänge in Festkörpern und des Lokalisierungseffekts von Licht in photonischen Geräten.
Der Autor hat durch Untersuchungen herausgefunden, dass KANs es sehr einfach machen, Mobilitätskanten zu extrahieren, sei es numerisch oder symbolisch.
Offensichtlich ist KAN zu einem leistungsstarken Assistenten und wichtigen Mitarbeiter für Wissenschaftler geworden.
Alles in allem wird KAN dank seiner Vorteile in Bezug auf Genauigkeit, Parametereffizienz und Interpretierbarkeit ein nützliches Modell/Werkzeug für KI+Wissenschaft sein.
Zukünftige weitere Anwendungen von KAN im wissenschaftlichen Bereich müssen noch erforscht werden.

Das obige ist der detaillierte Inhalt vonMLP wurde über Nacht getötet! MIT Caltech und andere revolutionäre KANs brechen Rekorde und entdecken mathematische Theoreme, die DeepMind zerstören. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

