Heim >Web-Frontend >js-Tutorial >Eine kurze Diskussion über die Implementierung von acht Hauptsortierungen in Javascript_Javascript-Fähigkeiten
Eine kurze Diskussion über die Implementierung von acht Hauptsortierungen in Javascript_Javascript-Fähigkeiten
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2016-05-16 16:02:111107Durchsuche
Einen Monat nach Beginn des Schuljahres habe ich oft davon geträumt, dass in schriftlichen Prüfungen Fragen zu Datenstrukturalgorithmen auftauchen. Ich habe mehr Angst vor Datenstrukturen als vor irgendwelchen „Geistern“. Haha, es scheint wirklich notwendig zu sein, häufig verwendete Datenstrukturen zu überprüfen, um zu verhindern, dass der „Albtraum“ wahr wird.
Unnötig zu erwähnen, wie wichtig Programmiergrundlagen wie Datenstrukturen sind. Kommen wir gleich zur Sache.
Der Sortieralgorithmus ist in interne Sortierung und externe Sortierung unterteilt. Die interne Sortierung nutzt Speicher, und hier wird nur die interne Sortierung besprochen.
1. Einfügungssortierung: direkte Einfügungssortierung und Hill-Sortierung
2. Auswahlsortierung: einfache Auswahlsortierung und Heap-Sortierung
3. Austauschsortierung: Blasensortierung und Schnellsortierung
4, Sortierung zusammenführen
5, Basissortierung

Direkte Einfügungssortierung
Grundidee: In einer zu sortierenden Zahlenmenge wird unter der Annahme, dass die vorherigen (n-1) [n>=2] Zahlen bereits in Ordnung sind, zuerst die n-te Zahl in die zuvor geordnete Zahl eingefügt, also dass diese n Zahlen auch sortiert sind. Wiederholen Sie diesen Zyklus, bis alles in Ordnung ist.
Hügelsortierung
Grundidee: Der Algorithmus unterteilt zunächst eine zu sortierende Zahlenmenge entsprechend einem bestimmten Inkrement d (n/2, n ist die zu sortierende Zahl) in mehrere Gruppen, und die in jeder Gruppe aufgezeichneten Indizes unterscheiden sich um d . Führen Sie eine direkte Einfügungssortierung für alle Elemente in jeder Gruppe durch, gruppieren Sie sie dann mit einem kleineren Inkrement (d/2) und führen Sie eine direkte Einfügungssortierung für jede Gruppe durch. Wenn das Inkrement auf 1 reduziert wird, ist die Sortierung nach der Direkteinfügungssortierung abgeschlossen.
Einfache Auswahlsortierung
Grundidee: Wählen Sie aus einer zu sortierenden Zahlenmenge die kleinste Zahl aus und tauschen Sie sie mit der Zahl an der ersten Position aus. Finden Sie dann die kleinste Zahl unter den verbleibenden Zahlen und tauschen Sie sie mit der Zahl an der zweiten Position aus , also Finden Sie haha bis zur vorletzten Zahl und der letzten Zahl.
Heap-Sortierung
Grundidee: Heap-Sortierung ist eine Baumauswahlsortierung, die eine wirksame Verbesserung gegenüber der Direktauswahlsortierung darstellt.
Eine Sequenz (h1, h2,...,hn) mit n Elementen, genau dann, wenn (hi>=h2i,hi>=2i 1) oder (hi<=h2i,hi<=2i 1 ) ( i=1,2,...,n/2) wird als Heap bezeichnet. Hier werden nur Halden besprochen, die die erstere Bedingung erfüllen. Aus der Definition eines Heaps geht hervor, dass das oberste Element des Heaps (dh das erste Element) das größte Element (Big Top Heap) sein muss. Ein vollständiger Binärbaum kann die Struktur eines Heaps sehr intuitiv darstellen. Die Oberseite des Heaps ist die Wurzel, die anderen sind der linke und der rechte Teilbaum. Zunächst wird die zu sortierende Zahlenfolge als sequentiell gespeicherter Binärbaum betrachtet und ihre Speicherreihenfolge so angepasst, dass sie zu einem Heap wird. Zu diesem Zeitpunkt ist die Anzahl der Wurzelknoten des Heaps am größten. Tauschen Sie dann den Wurzelknoten mit dem letzten Knoten des Heaps aus. Passen Sie dann die vorherigen (n-1) Zahlen erneut an, um einen Heap zu bilden. Und so weiter, bis es einen Heap mit nur zwei Knoten gibt, diese ausgetauscht werden und schließlich eine geordnete Folge von n Knoten erhalten wird. Aus der Beschreibung des Algorithmus geht hervor, dass die Heap-Sortierung zwei Prozesse erfordert: Der eine besteht darin, den Heap einzurichten, und der andere darin, die Positionen zwischen der Oberseite des Heaps und dem letzten Element des Heaps auszutauschen. Die Heap-Sortierung besteht also aus zwei Funktionen. Eine davon ist die Penetrationsfunktion zum Aufbau des Heaps, die andere ist die Funktion zum wiederholten Aufrufen der Penetrationsfunktion zur Implementierung der Sortierung.
Blasensortierung
Grundidee: Vergleichen Sie in einem zu sortierenden Zahlensatz die beiden benachbarten Zahlen der Reihe nach von oben nach unten und passen Sie sie für alle Zahlen im Bereich an, die noch nicht sortiert wurden, sodass die größeren Zahlen sinken. und die kleineren steigen auf. Das heißt: Immer wenn zwei benachbarte Zahlen verglichen werden und sich herausstellt, dass ihre Reihenfolge der Reihenfolgeanforderung entgegengesetzt ist, werden sie vertauscht.
Schnellsortierung
Grundidee: Wählen Sie ein Benchmark-Element aus, normalerweise das erste oder letzte Element, und teilen Sie die zu sortierende Sequenz durch einen Scan in zwei Teile, wobei ein Teil kleiner als das Benchmark-Element und der andere Teil größer ist als oder gleich dem Benchmark-Element. Zu diesem Zeitpunkt befinden sich die Benchmark-Elemente an ihren korrekten sortierten Positionen, und dann werden die beiden geteilten Teile auf die gleiche Weise rekursiv sortiert.
Sortierung zusammenführen
Grundlegende Sortierung: Die Methode der Zusammenführungssortierung besteht darin, zwei (oder mehr) geordnete Listen zu einer neuen geordneten Liste zusammenzuführen, dh die zu sortierende Sequenz wird in mehrere Untersequenzen unterteilt, wobei jede Untersequenz sequentiell ist. Fügen Sie dann die geordneten Teilsequenzen zur geordneten Gesamtsequenz zusammen.
Radix-Sortierung
Grundidee: Alle zu vergleichenden Werte (positive ganze Zahlen) auf die gleiche Ziffernlänge vereinheitlichen und vor Zahlen mit kürzeren Ziffern Nullen hinzufügen. Sortieren Sie sie dann, beginnend mit dem niedrigsten Bit, einzeln. Auf diese Weise wird die Sequenz nach der Sortierung vom niedrigsten zum höchsten Bit zu einer geordneten Sequenz.
Code-Demonstrationsadresse: http://lovermap.sinaapp.com/test/sort.html
Jetzt analysieren wir die Stabilität von 8 Sortieralgorithmen.
(Internetnutzer werden gebeten, die Stabilität des Sortierens zu verstehen, indem sie die Grundideen des Sortierens zuvor kombinieren (die Grundideen der 8 Sortierarten wurden bereits erwähnt und werden hier nicht wiederholt), sonst kann es etwas vage sein)
(1) Direkte Einfügungssortierung : Bei der allgemeinen Einfügungssortierung beginnt der Vergleich mit dem letzten Element der geordneten Sequenz. Wenn es größer ist, wird es direkt dahinter eingefügt, andernfalls bleibt es erhalten vorwärts vergleichen. Wenn ein Element gefunden wird, das dem eingefügten Element entspricht, wird es nach dem gleichen Element eingefügt. Die Einfügungssortierung ist stabil.
(2) Hill-Sortierung : Die Hill-Sortierung ist eine Einfügungssortierung von Elementen nach unterschiedlichen Synchronisationslängen. Eine Einfügungssortierung ist stabil und ändert die relative Reihenfolge derselben Elemente nicht, jedoch in unterschiedlicher Reihenfolge Beim Einfügungssortierungsprozess können sich dieselben Elemente in ihrer jeweiligen Einfügungssortierung bewegen und die Stabilität wird zerstört, sodass die Hill-Sortierung instabil ist.
(3) Einfache Auswahlsortierung : Wenn in einer Auswahl das aktuelle Element kleiner als ein Element ist und das kleine Element hinter einem Element erscheint, das dem aktuellen Element entspricht, bleibt es danach stabil Austausch Sex wird zerstört. Es kann etwas vage sein, es einfach auszudrücken, schauen wir uns ein kleines Beispiel an: 858410, im ersten Scan wird das erste Element 8 durch 4 ausgetauscht, dann stimmt die relative Reihenfolge der beiden 8er in der Originalsequenz nicht mit überein die ursprüngliche Reihenfolge, daher ist die Auswahlsortierung nicht möglich. Stabilisieren.
(4) Heap-Sortierung : Der Prozess der Heap-Sortierung besteht darin, den größten (Big-Top-Heap) oder den Kleinsten (Small-Top-Heap) auszuwählen, beginnend mit dem n/2 und seinen untergeordneten Knoten mit a Insgesamt 3 Werte. Die Wahl zwischen 3 Elementen zerstört sicherlich nicht die Stabilität. Bei der Auswahl von Elementen für die übergeordneten Knoten n/2-1, n/2-2, ... ist es jedoch möglich, dass der n/2-te übergeordnete Knoten das nächste Element austauscht, der n/2-1-te übergeordnete Knoten jedoch nicht Tauschen Sie am Ende dasselbe Element aus, sodass die Heap-Sortierung nicht stabil ist.
(5) Blasensortierung : Wie aus dem vorherigen Inhalt hervorgeht, handelt es sich bei der Blasensortierung um einen Vergleich zweier benachbarter Elemente, und wenn die beiden Elemente gleich sind, findet auch ein Austausch statt. Kein Umtausch nötig. Die Blasensortierung ist also stabil.
(6) Schnelle Sortierung : Wenn das zentrale Element mit einem Element in der Sequenz ausgetauscht wird, ist es sehr wahrscheinlich, dass die Stabilität des vorherigen Elements gestört wird. Schauen wir uns ein kleines Beispiel an: 6 4 4 5 4 7 8 9. Im ersten Sortierdurchgang wird durch den Austausch des zentralen Elements 6 und des dritten Elements 4 die ursprüngliche Reihenfolge von Element 4 zerstört, sodass die schnelle Sortierung instabil ist.
(7) Zusammenführungssortierung : Wenn in der zerlegten Unterspalte 1 oder 2 Elemente vorhanden sind, wird 1 Element nicht ausgetauscht, und 2 Elemente werden nicht ausgetauscht, wenn sie gleich groß sind . Wenn während des Sequenzzusammenführungsprozesses die beiden aktuellen Elemente gleich sind, speichern wir die Elemente der vorherigen Sequenz vor der Ergebnissequenz, sodass auch die Zusammenführungssortierung stabil ist.
(8) Radix-Sortierung : Zuerst nach niedriger Reihenfolge sortieren, dann nach hoher Reihenfolge sortieren und dann bis zur höchsten Reihenfolge sortieren. Manchmal haben einige Attribute eine Prioritätsreihenfolge. Sie werden zuerst nach niedriger Priorität und dann nach hoher Priorität sortiert. Die endgültige Reihenfolge ist, dass diejenigen mit hoher Priorität zuerst kommen und diejenigen mit der gleichen hohen und niedrigen Priorität zuerst. Die Radix-Sortierung basiert auf getrennter Sortierung und getrennter Sammlung und ist daher stabil.
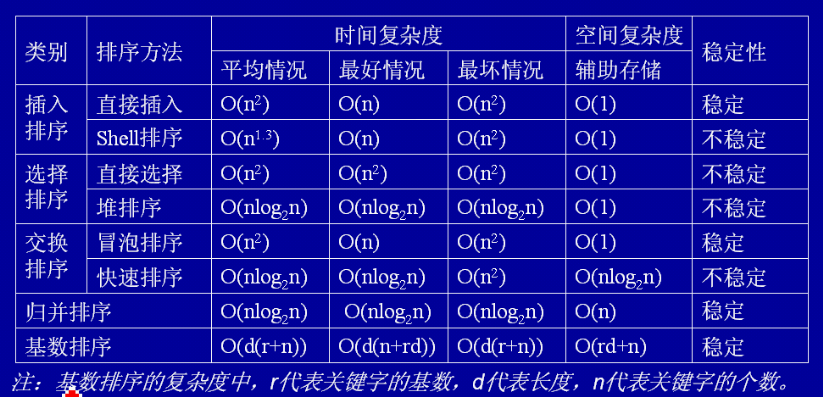
Zusammenfassung der Klassifizierung, Stabilität, Zeitkomplexität und Raumkomplexität von 8 Sortierarten:
Das Obige ist der gesamte Inhalt dieses Artikels. Ich hoffe, er gefällt Ihnen allen.
In Verbindung stehende Artikel
Mehr sehen- Eine eingehende Analyse der Bootstrap-Listengruppenkomponente
- Detaillierte Erläuterung des JavaScript-Funktions-Curryings
- Vollständiges Beispiel für die Generierung von JS-Passwörtern und die Erkennung der Stärke (mit Download des Demo-Quellcodes)
- Angularjs integriert WeChat UI (weui)
- Wie man mit JavaScript schnell zwischen traditionellem Chinesisch und vereinfachtem Chinesisch wechselt und wie Websites den Wechsel zwischen vereinfachtem und traditionellem Chinesisch unterstützen – Javascript-Kenntnisse

