Der Vorgang zur Überprüfung der perfekten Quadratformel mit dem Geometrischen Skizzenblock

PHP-Editor Xigua verrät Ihnen die geheime Strategie zum Freischalten aller Fähigkeiten von Winter Rhapsody. Dieses Charakter-Plot-Simulationsspiel basiert auf einer Kleinstadtgeschichte und enthält japanische Elemente. Die Spieler stehen vor der Herausforderung, Rätsel bis in die Tiefe zu lösen, wobei Geschicklichkeit zum Schlüsselfaktor wird. Das Spiel enthält umfangreiche und interessante Funktionen und bietet eine Vielzahl von Fähigkeiten zum Spielen, um alle Fähigkeiten für ein umfassenderes Spielerlebnis freizuschalten!

Erstellen Sie neue Parameter a und b. Öffnen Sie den geometrischen Skizzenblock, führen Sie den Befehl [Daten]-[Neuer Parameter] aus, geben Sie den Parameternamen a in das Popup-Dialogfeld ein, der Wert ist 6 und die Einheit ist der Abstand. Erstellen Sie auf diese Weise einen neuen Parameter b=2,00 cm und führen Sie den Befehl [Daten]-[Berechnen] aus, um den Wert von a+b zu berechnen.

Verwenden Sie den Wert von a+b als Seitenlänge, um a zu konstruieren Quadrat. Wählen Sie mit dem Verschieben-Werkzeug den berechneten Wert aus und führen Sie den Befehl [Transformieren] – [Markierungsabstand] aus. Zeichnen Sie mit dem Punktwerkzeug einen beliebigen Punkt A auf dem Zeichenbrett, wählen Sie den Punkt aus und führen Sie den Befehl [Transformieren] – [Übersetzen] aus, ändern Sie den Winkel im Popup-Dialogfeld auf 0 und klicken Sie auf „OK“, um Punkt B zu erhalten. Konstruieren Sie das Liniensegment AB, doppelklicken Sie auf Punkt A, um das Rotationszentrum zu markieren, wählen Sie das Liniensegment AB aus und führen Sie den Befehl [Transformieren] - [Drehen] aus. Der Winkel beträgt 90 und klicken Sie auf OK, um Punkt D zu erhalten. Wählen Sie Punkt D und das Liniensegment AB aus, um eine parallele Linie zu konstruieren. Wählen Sie außerdem Punkt B und das Liniensegment AD aus, um eine parallele Linie zu konstruieren. Konstruieren Sie die Liniensegmente BC und CD, um ein Quadrat ABCD zu erstellen.

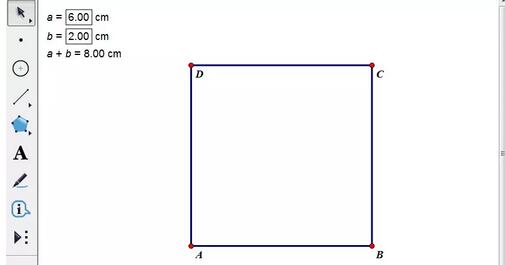
Teile das Quadrat. Wählen Sie Parameter a und führen Sie den Befehl [Transformieren] – [Markierungsabstand] aus. Wählen Sie Punkt A aus und führen Sie den Befehl [Transformieren] – [Translation] aus. Klicken Sie im Popup-Dialogfeld auf „OK“, um Punkt A zu erhalten '. Wählen Sie Parameter b und führen Sie den Befehl [Transformieren]-[Markierungsabstand] aus. Wählen Sie Punkt C aus und führen Sie den Befehl [Transformieren]-[Translation] aus. Im Popup-Dialogfeld beträgt der Winkel 180. Klicken Sie auf OK, um Punkt C zu erhalten '. Konstruieren Sie eine parallele Linie zur Seite AB durch Punkt A‘, konstruieren Sie eine parallele Linie zur Seite AD durch Punkt C‘ und erhalten Sie den Schnittpunkt E. Blenden Sie die parallelen Linien aus und konstruieren Sie die Liniensegmente wie unten gezeigt.

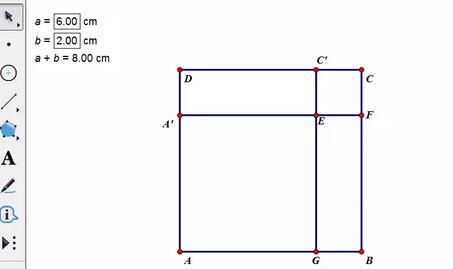
Berechnen Sie die Fläche des Quadrats ABCD und die Flächen der darin unterteilten vier Vierecke. Die Fläche des Quadrats ABCD kann ausgedrückt werden als: (a+b)*(a+b) und ihr Wert kann durch Berechnung ermittelt werden. Durch Berechnung kann geschlossen werden, dass die Flächen der vier kleinen Vierecke sind: ab, ab, a2, b2. Durch Addition der Flächen der vier kleinen Vierecke sollte der erhaltene Wert gleich der Fläche des Quadrats ABCD sein , damit die Vollständigkeit der Quadratformel überprüft werden kann.

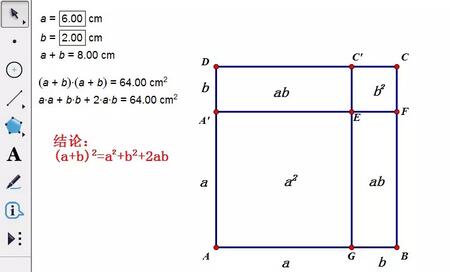
Das obige ist der detaillierte Inhalt vonDer Vorgang zur Überprüfung der perfekten Quadratformel mit dem Geometrischen Skizzenblock. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!