KI untergräbt die mathematische Forschung! Der Gewinner der Fields-Medaille und der chinesisch-amerikanische Mathematiker führten 11 hochrangige Arbeiten an | Gefällt mir bei Terence Tao

KI verändert tatsächlich die Mathematik.

Kürzlich hat Terence Tao, der diesem Thema große Aufmerksamkeit geschenkt hat, die neueste Ausgabe des „Bulletin of the American Mathematical Society“ weitergeleitet.

Zum Thema „Werden Maschinen die Mathematik verändern?“ äußerten viele Mathematiker ihre Meinung. Der gesamte Prozess war voller Funken, knallhart und spannend.

Der Autor hat eine starke Besetzung, darunter der Fields-Medaillengewinner Akshay Venkatesh, der chinesische Mathematiker Lejun Zheng, der Informatiker Ernest Davis von der New York University und viele andere bekannte Wissenschaftler der Branche.

Die Welt der KI hat weltbewegende Veränderungen erfahren. Viele dieser Artikel wurden vor einem Jahr eingereicht, und in diesem Jahr hat die KI viele bedeutende Veränderungen erfahren.

Trotzdem sind diese Artikel immer noch voller Gold und brachten sogar Terence Tao zum Schreien: „Dieses Feld bewegt sich zu schnell!“ Lässt meine unveröffentlichten Artikel überflüssig erscheinen.

Niemand kann leugnen, dass KI-Tools den Bereich der Mathematik in alarmierendem Tempo voranbringen.

Wird künstliche Intelligenz zu einer Revolution in der Art und Weise führen, wie Informationen in wissenschaftlichen Bereichen, einschließlich der reinen Mathematik, gesammelt und verarbeitet werden? Wird es die Art und Weise verändern, wie Mathematik betrieben wird?

Mathematiker sind gespalten: Einige glauben, dass ein weit verbreiteter Einsatz von maschinellem Lernen in der Forschung unmittelbar bevorsteht, während andere skeptisch sind und sich an den übermäßigen Optimismus und den darauf folgenden „KI-Winter“ erinnern.

Allerdings ist es sehr wahrscheinlich, dass es in der Praxis der mathematischen Forschung zu drastischen Veränderungen kommen wird. Jetzt ist es an der Zeit, dass Mathematiker sich mit den Problemen befassen, die diese Veränderungen mit sich bringen.

Kein Zweifel, der Sturm steht bevor.

Werden Maschinen die Mathematik verändern?

Der Einfluss der mathematischen Automatisierung auf die mathematische Forschung

In diesem Artikel untersucht der Fields-Medaillengewinner Akshay Venkatesh den Einfluss der Automatisierung auf die mathematische Forschung.

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01834-5/S0273-0979-2024-01834-5. pdf

In diesem Artikel schlug Akshay Venkatesh ein interessantes Gedankenexperiment vor –

Im Jahr 2017 brachte sich Alphazero von DeepMind über Nacht Schach und Go bei und übertraf damit die Menschen.

Was wäre, wenn zehn Jahre später auch „Alephzero“ (geschrieben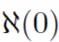) die gleiche formatierte Mathematik anwenden würde?

Das „Mathematik“ in diesem Artikel bezieht sich auf „reine mathematische Forschung“.

Unser Ausgangspunkt ist die Annahme, dass „Alephzero“ sich selbst Mathematik an der High School und am College beigebracht und alle Übungen der Reihe „Graduate Terts in Mathematics“ des SpringerVerlags abgeschlossen hat. Am nächsten Morgen veröffentlichten die Mathematiker es, die Kinder luden es herunter und führten es mit unseren Computerressourcen aus.

Das ist in der Tat ein Gedankenexperiment, weil es offensichtlich unrealistisch ist: Indem wir unseren Horizont auf die nächsten zehn oder zwanzig Jahre beschränken, erlauben wir uns, uns von den gesellschaftlichen Veränderungen zu lösen, die mit solchen technologischen Fortschritten einhergehen können. Das Nachdenken über dieses Problem ermöglicht es uns auch um nicht an extremere Arten maschineller Intelligenz zu denken, bei denen wir Alephzero eher als Elektrowerkzeug denn als lebenden Kollaborateur modellieren.

Wir können uns auf diese Weise trösten: Tatsächlich ist diese Prämisse zu weit von uns entfernt und wir müssen nicht darüber nachdenken. Aber wenn wir auch nur die geringste Chance zulassen, könnte dies in zwanzig Jahren passieren.

Bietet ein sehr grobes Modell, das einen Teil unseres Wertmechanismus durch Bayes'sche Interaktionen in Mathematikern und Problemnetzwerken veranschaulicht. Wir überlegen nun, wie sich „Alephzero“ auf dieses Netzwerk auswirken und das Ergebnis verändern wird.

Wie wir sehen, ist die wahrgenommene Schwierigkeit ein wichtiger Teil unserer Wertschöpfung.

Unabhängig von der konkreten Situation wird „Alephzero“ unsere Fähigkeit, Probleme zu lösen, und damit auch unsere Wahrnehmung der Schwierigkeit des Problems verändern.

Die Teile des mathematischen Prozesses, die am schnellsten beschleunigt werden können, werden die größte Verringerung ihrer wahrgenommenen Schwierigkeit erfahren, und gemäß unserem obigen Modell wird der Staat die größte Verringerung erleiden. Ein ähnliches Muster tritt in vielen Fällen der Automatisierung auf.

Schließlich wird „Alephzero“ das gesamte Spektrum interessanter Probleme in der Mathematik erheblich erweitern. Es würde gleiche Wettbewerbsbedingungen zwischen professionellen Mathematikern und allen anderen schaffen.

Wie Maschinen Mathematik aggregierter machen können

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01827-8 / S0273-0979-2024-01827-8.pdf

Der Mathematiker Zheng Lejun glaubt, dass wir diese Technologie nutzen können, um Mathematik stärker „aggregiert“ zu machen, da die Technologie die Art und Weise, wie wir Mathematik studieren, verändert hat, und das ist auch der Fall Es geht nicht darum, menschliche Mathematiker angesichts des technologischen Fortschritts überflüssig zu machen.

Als sie darüber nachdachte, was es bedeutet, „Mathematik zu betreiben“, untersuchte sie die folgenden Aspekte der mathematischen Technologie: Lehren und Lernen, Fragen stellen, zusammenarbeiten, kommunizieren und den Akt der Forschung.

Dies ist keine strenge Analyse, sondern eine weise Überlegung, die auf ihrer Erfahrung als Mathematikerin basiert.

Lejun Zheng glaubt, dass es zwar einige computergestützte Beweisprüfer und sogar Beweisgeneratoren gibt, die Technologie jedoch nicht wirklich in die tiefgreifendsten, kreativsten und menschlichsten Aspekte der mathematischen Forschung eingedrungen ist.

Der tiefe kreative Teil besteht zunächst darin, Ideen zu entwickeln – Ideen für Definitionen, Ideen für Beweise, Ideen für die Herstellung von Verbindungen zwischen verschiedenen Teilen der Mathematik, Ideen für neue Ausdrucksweisen, Ideen für Symbole und Terminologie, Ideen für grafisches Denken sowie Ideen zur visuellen Darstellung.

Damit Maschinen mathematische Forschung betreiben können, müssen wir einen Weg finden, ihnen zu sagen, dass sie es tun sollen. Es ist schwierig, ihnen zu sagen, wie sie es tun sollen, wenn wir nicht selbst wissen, wie sie es tun sollen.

Maschinen können ein gewisses Maß an Beweisprüfung durchführen, aber insgeheim wissen Mathematiker, dass wir keine völlig strengen Beweise schreiben können – wir argumentieren auf der Grundlage der Logik und führen logische Schritte aus, von denen wir glauben, dass unsere Kollegen sie auch befolgen werden einspringen können. Unterstützung.

Wir legen die Größe dieser Schritte nicht fest, daher ist es schwierig, der Maschine zu sagen, dass sie dies tun soll.

Das Erstellen von Beweisen ist eine ganz andere Fähigkeit, als sie nur zu überprüfen, wie jeder Mathematikstudent weiß. Es ist viel einfacher, den Beweisen einer anderen Person zu folgen, als selbst eine neue zu erfinden. Das soll nicht heißen, dass Computer menschliche Mathematiker in ihren mathematischen Forschungsfähigkeiten niemals übertreffen können.

Was Computer ihrer Meinung nach leistungsfähiger macht als menschliche Mathematiker, ist Folgendes:

Sie haben eine größere Fähigkeit, alle möglichen Aktionen zu durchsuchen, indem sie alle derzeit bekannten möglichen logischen Ergebnisse durchsuchen. Sie können versuchen, neue Mathematik zu entwickeln .

Dies erfordert einen Sprung an Vorstellungskraft, Rätselraten und Intuition. Was würde ein Computer ausreichen, um dies zu tun? Die Idee ist sehr interessant.

Können Computer uns beim logischen Denken helfen

?

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01833-3/S0273-0979-2024-01833-3.pdf

Computer haben die Art und Weise, wie wir mathematische Forschung durchführen, revolutioniert und komplexe Berechnungen zum Kinderspiel gemacht.

Aber werden sie als nächstes zu Assistenten für unser logisches Denken? Könnten sie eines Tages überhaupt unabhängig argumentieren?

Dieser Artikel gibt Ihnen einen Überblick über die jüngsten wichtigen Fortschritte bei neuronalen Netzen, Computer-Theorembeweisen und großen Sprachmodellen.

Wie formale Tools uns helfen können, bessere mathematische Forschung zu betreiben

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273- 0979- 2024-01832-1/S0273-0979-2024-01832-1.pdf

Seit Beginn des 20. Jahrhunderts haben wir verstanden, dass mathematische Definitionen und Beweise durch formale Systeme mit strenger Syntax und erreicht werden können Regeln werden dargestellt.

Auf dieser Grundlage ermöglicht uns die Entwicklung von Computerbeweisassistenten, mathematisches Wissen in digitaler Form zu kodieren.

In diesem Artikel wird untersucht, wie diese Art von Technologie und die damit verbundenen Tools uns dabei helfen können, bessere mathematische Forschung durchzuführen.

Verwenden Sie Theorembeweiser, um komplexe Probleme in der mathematischen Forschung zu vereinfachen

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/ S0273- 0979-2024-01831-X/S0273-0979-2024-01831-X.pdf

In diesem Artikel wird untersucht, wie ein interaktiver Theorembeweis verwendet werden kann, um komplexe Probleme in der mathematischen Forschung durch die Festlegung abstrakter Grenzen zu vereinfachen.

Seltsames neues Universum: LLM ermöglicht Mathematikern, mit Beweisassistenten in natürlicherer Sprache zu kommunizieren

Papieradresse: https://www.ams.org/journals/bull/2024-61 - 02/S0273-0979-2024-01830-8/S0273-0979-2024-01830-8.pdf

Aktuelle Computerprogramme, auch Beweisassistenten genannt, sind in der Lage, die Richtigkeit mathematischer Beweise zu überprüfen, Doch die spezielle Beweissprache, die sie verwenden, stellt für viele Mathematiker ein Hindernis dar.

Große Sprachmodelle (LLMs) haben das Potenzial, diese Barriere zu überwinden und es Mathematikern zu ermöglichen, mit Beweisassistenten in natürlicherer Sprache zu kommunizieren. Dies fördert nicht nur ihre Intuition, sondern stellt auch sicher, dass ihre Argumentation richtig ist.

Verwenden Sie Deep-Learning-Tools, um reine mathematische Forschung durchzuführen

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024 - 01829-1/S0273-0979-2024-01829-1.pdf

In diesem Artikel geht es um persönliche Erfahrungen und den informellen Austausch darüber, was ein reiner Mathematiker erwarten könnte, wenn er versucht, Deep-Learning-Tools in der Forschung einzusetzen.

Kann KI mathematische Forschung betreiben

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01828-X/S0273-0979-2024-01828-X.pdf

Dieser Artikel untersucht die Fähigkeiten und Grenzen der aktuellen KI-Technologie bei der Lösung von Textproblemen, die grundlegende Mathematik und gesundes Denken kombinieren.

Der Autor bespricht drei Methoden, die mithilfe der KI-Technologie für natürliche Sprache entwickelt wurden: direktes Geben von Antworten, Generieren von Computerprogrammen, die Probleme lösen, und Generieren formaler Darstellungen, die von automatisierten Theorem-Testern verwendet werden können.

Der Autor ist der Ansicht, dass die Bedeutung dieser Einschränkungen bei der Entwicklung der KI-Technologie für die rein mathematische Forschung noch nicht klar definiert ist, sie jedoch bei mathematischen Anwendungen äußerst kritisch sind und auch bei der Entwicklung von Programmen wichtig sind, die mathematische Inhalte verstehen können von Menschen geschrieben. „Was ist Beweis im Maschinenzeitalter?“ /S0273-0979-2024-01826-6.pdf

In diesem Artikel untersucht der Autor die Natur von Beweisen und ihre Entwicklung im Maschinenzeitalter, indem er die Werte in der traditionellen Verifizierung und der Computerverifizierungsanalyse gegenüberstellt.

Die in dem Artikel schließlich vorgeschlagene Methode könnte es Computern ermöglichen, erfolgreiche Strategien zu beweisen, die auf menschlicher Erfahrung basieren.

Automatisierung ermöglicht es Mathematikern, über ihren eigenen Wert nachzudenken

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01825 -4/S0273-0979-2024-01825-4.pdf

In diesem Artikel kritisiert der Autor scharf das mangelnde Denken von Kollegen, insbesondere wenn es um die mechanisierte Zukunft der Mathematik geht Künstliche Intelligenz auf einer breiteren Ebene in der Gesellschaft.

Fortsetzungsbrüche in p-adischen Zahlenfeldern

Papieradresse: https://www.ams.org/journals/bull/2024-61-02/S0273-0979-2024-01819 - 9/S0273-0979-2024-01819-9.pdf

Fortgesetzte Brüche haben eine lange Geschichte in der Zahlentheorie, insbesondere im Bereich der diophantischen Näherung.

Dieser Artikel zielt darauf ab, die Kernergebnisse der p-adischen Kettenbruchtheorie zu skizzieren, bei der es sich um einen Kettenbruch handelt, der auf dem p-adischen Zahlenkörper Qp definiert ist.

Der Inhalt beginnt mit grundlegenden Konzepten und stellt die neuesten Fortschritte und offenen Probleme vor, mit denen derzeit konfrontiert ist.

Tao Zhexuan hat gepostet: Maschinengestützter Beweis

Übrigens hat Tao Zhexuan auch den „Maschinengestützten Beweis“ des Artikels verwendet, den er zuvor geschrieben hat.

Papieradresse: https://terrytao.files.wordpress.com/2024/03/machine-assisted-proof-notices.pdf

In diesem Artikel sagte Tao Zhexuan, dass sie mithilfe der Fähigkeit von LLM, Eingaben in natürlicher Sprache zu verarbeiten, wahrscheinlich zu einer benutzerfreundlichen Plattform werden werden, die es Mathematikern ohne spezifische Softwarekenntnisse ermöglicht, fortschrittliche Tools zu verwenden.

Mittlerweile sind er und viele Wissenschaftler daran gewöhnt, diese Modelle zu verwenden, um einfache Codes in verschiedenen Sprachen zu generieren, einschließlich symbolischer Algebra-Pakete, oder um komplexe Diagramme und Bilder zu erstellen.

Da die formelle Beweisüberprüfung derzeit stark auf menschliche Anstrengungen angewiesen ist, ist es derzeit unpraktisch, eine große Anzahl aktueller Forschungsarbeiten in Echtzeit vollständig zu formalisieren.

Im Bereich partieller Differentialgleichungen ist es oft notwendig, Integralausdrücke mit einer oder mehreren unbekannten Funktionen (z. B. die Lösung einer PDE) über mehrere Berechnungsseiten abzuschätzen.

Dazu gehört die Verwendung der Grenzen dieser Funktionen in verschiedenen Funktionsraumnormen (z. B. der Sobolev-Raumnorm), kombiniert mit Standardungleichungen (z. B. Hölder-Ungleichung und Sobolev-Ungleichung) und beispielsweise partiellen Integral- oder Integralzeichen-Differentialgleichungen .

Obwohl es sich bei dieser Art von Berechnung um einen Routinevorgang handelt, kann er Fehler unterschiedlichen Ausmaßes enthalten (z. B. Vorzeichenfehler). Es ist für Prüfer mühsam und zeitaufwändig, diese Berechnungen im Detail zu überprüfen, und diese Berechnungen selbst sind in Abgesehen von der Tatsache, dass die Schätzung korrekt ist, ist es schwierig, ein tieferes mathematisches Verständnis oder einen tieferen Einblick zu vermitteln.

Es ist denkbar, dass in Zukunft Tools entwickelt werden, um mathematische Schätzungen automatisch oder halbautomatisch zu erstellen und die derzeit langwierigen und wenig inspirierenden Schätzungsnachweise durch einen Link zu einem formellen Nachweiszertifikat zu ersetzen.

Wenn wir noch einen Schritt weiter gehen, können wir vielleicht davon ausgehen, dass ein zukünftiges KI-Tool auf der Grundlage einer ersten Reihe von Annahmen und Methoden in der Lage sein wird, die bestmögliche Schätzung abzugeben, ohne dass dafür zunächst Papierkram erledigt werden muss -und-Bleistift-Berechnungen, um vorherzusagen, was diese Schätzung sein könnte.

Derzeit ist der geschätzte mögliche Zustandsraum zu komplex, um ihn automatisch zu erkunden, aber mit der Entwicklung der Technologie ist die Möglichkeit, eine solche automatisierte Erkundung zu realisieren, nicht außer Reichweite.

Nach der Implementierung werden wir in der Lage sein, mathematische Untersuchungen in einem Umfang durchzuführen, der derzeit undurchführbar erscheint.

Nehmen wir als Beispiel partielle Differentialgleichungen. Die aktuelle Forschung untersucht normalerweise nur eine oder zwei Gleichungen gleichzeitig, aber in Zukunft können wir möglicherweise Hunderte von Gleichungen gleichzeitig untersuchen.

Entwickeln Sie beispielsweise zunächst ein vollständiges Argument für eine Gleichung und lassen Sie das KI-Tool diese Argumente dann gegebenenfalls an eine große Anzahl verwandter Gleichungsfamilien anpassen, wenn bei der Erweiterung des Arguments unkonventionelle Situationen auftreten. Die KI wird dem Autor Fragen stellen.

In anderen Bereichen der Mathematik, beispielsweise der Graphentheorie, zeichnen sich bereits erste Anzeichen dieser groß angelegten mathematischen Erkundung ab.

Allerdings lassen sich diese aktuellen Vorversuche nur schwer in großem Maßstab vorantreiben, da sie auf extrem rechenintensiven KI-Modellen basieren oder ein hohes Maß an menschlicher Beteiligung und Aufsicht auf Expertenebene erfordern.

Terence Tao glaubt jedoch, dass wir in naher Zukunft die Geburt innovativerer maschinengestützter mathematischer Methoden erleben werden.

Das obige ist der detaillierte Inhalt vonKI untergräbt die mathematische Forschung! Der Gewinner der Fields-Medaille und der chinesisch-amerikanische Mathematiker führten 11 hochrangige Arbeiten an | Gefällt mir bei Terence Tao. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!