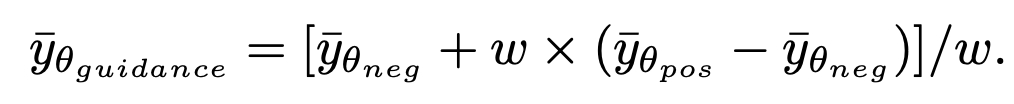Das Diffusionsmodell eröffnet mit seiner hervorragenden Leistung bei der Bilderzeugung eine neue Ära generativer Modelle. Große Modelle wie Stable Diffusion, DALLE, Imagen, SORA usw. sind entstanden und haben die Anwendungsaussichten generativer KI weiter bereichert. Aktuelle Diffusionsmodelle sind jedoch theoretisch nicht perfekt, und nur wenige Studien haben sich mit dem Problem undefinierter Singularitäten an den Endpunkten der Abtastzeit befasst. Darüber hinaus wurden der durchschnittliche Grauwert, der durch das Singularitätsproblem in der Anwendung verursacht wird, und andere Probleme, die sich auf die Qualität des generierten Bildes auswirken, nicht gelöst. Um dieses Problem zu lösen, arbeitete das WeChat Vision-Team mit der Sun Yat-sen-Universität zusammen, um gemeinsam das Singularitätsproblem im Diffusionsmodell zu untersuchen, und schlug eine Plug-and-Play-Methode vor, die das Sampling-Problem am effektiv löste Anfangsmoment. Diese Methode löst erfolgreich das Problem der durchschnittlichen Graustufen und verbessert die Generierungsfähigkeit vorhandener Diffusionsmodelle erheblich. Die Forschungsergebnisse wurden auf der CVPR 2024-Konferenz vorgestellt. Diffusionsmodelle haben bemerkenswerte Erfolge bei multimodalen Inhaltsgenerierungsaufgaben erzielt, einschließlich der Bild-, Audio-, Text- und Videogenerierung. Die erfolgreiche Modellierung dieser Modelle beruht größtenteils auf der Annahme, dass der umgekehrte Prozess des Diffusionsprozesses auch den Gaußschen Eigenschaften entspricht. Diese Hypothese wurde jedoch nicht vollständig bewiesen. Insbesondere am Endpunkt, also bei t=0 oder t=1, tritt das Singularitätsproblem auf, das die vorhandenen Methoden zur Untersuchung der Stichprobe an der Singularität einschränkt. Darüber hinaus wirkt sich das Singularitätsproblem auch auf die Generierungsfähigkeit des Diffusionsmodells aus, was dazu führt, dass das Modell das durchschnittliche Graustufenproblem aufweist, das heißt, es ist schwierig, Bilder mit starker oder schwacher Helligkeit zu erzeugen in der folgenden Abbildung dargestellt. Dies schränkt auch den Anwendungsbereich aktueller Diffusionsmodelle in gewissem Maße ein. Um das Singularitätsproblem des Diffusionsmodells am Zeitendpunkt zu lösen, arbeitete das WeChat-Vision-Team mit der Sun Yat-sen-Universität zusammen und führte eingehende Forschungen sowohl unter theoretischen als auch unter praktischen Gesichtspunkten durch. Zunächst schlug das Team eine Fehlerobergrenze vor, die eine ungefähre Gaußsche Verteilung des Umkehrprozesses im Singularitätsmoment enthält, was eine theoretische Grundlage für nachfolgende Forschungen lieferte. Basierend auf dieser theoretischen Garantie untersuchte das Team die Probenahme an singulären Punkten und kam zu zwei wichtigen Schlussfolgerungen: 1) Der singuläre Punkt bei t=1 kann durch Finden des Grenzwerts in einen abnehmbaren singulären Punkt umgewandelt werden, 2) die Singularität bei t=0 ist eine inhärente Eigenschaft des Diffusionsmodells und muss nicht vermieden werden. Basierend auf diesen Schlussfolgerungen schlug das Team eine Plug-and-Play-Methode vor: SingDiffusion, um das Problem der Abtastung des Diffusionsmodells im ersten Moment zu lösen. Eine große Anzahl experimenteller Überprüfungen hat gezeigt, dass das SingDiffusion-Modul mit nur einem Training nahtlos auf bestehende Diffusionsmodelle angewendet werden kann, wodurch das Problem des durchschnittlichen Grauwerts erheblich gelöst wird. Ohne den Einsatz klassifikatorfreier Leittechnologie kann SingDiffusion die Generierungsqualität aktueller Methoden erheblich verbessern, insbesondere nach der Anwendung auf Stable Diffusion1.5 (SD-1.5) wird die Qualität der generierten Bilder um 33 % verbessert Papieradresse: https://arxiv.org/pdf/2403.08381.pdf
 Projektadresse: https://pangzecheung.github.io/SingDiffusion/Papiertitel: Tackling the Singularities at the Endpoints of Time Intervals in Diffusion Modelle: Gaußsche Eigenschaften des inversen Prozesses Eigenschaften. Definieren Sie zunächst
Projektadresse: https://pangzecheung.github.io/SingDiffusion/Papiertitel: Tackling the Singularities at the Endpoints of Time Intervals in Diffusion Modelle: Gaußsche Eigenschaften des inversen Prozesses Eigenschaften. Definieren Sie zunächst als Trainingsprobe des Diffusionsmodells. Die Verteilung der Trainingsprobe kann ausgedrückt werden als:
Wobei δ die Dirac-Funktion darstellt. Gemäß der Definition des kontinuierlichen Zeitdiffusionsmodells in [1] kann der Vorwärtsprozess für zwei beliebige Momente 0≤s,t≤1 ausgedrückt werden als: wobei  ,
,  ,
,  ,
,  monoton mit sind Zeitwechsel von 1 auf 0. Unter Berücksichtigung der soeben definierten Trainingsmusterverteilung kann die Einzelmoment-Grenzwahrscheinlichkeitsdichte von
monoton mit sind Zeitwechsel von 1 auf 0. Unter Berücksichtigung der soeben definierten Trainingsmusterverteilung kann die Einzelmoment-Grenzwahrscheinlichkeitsdichte von  wie folgt ausgedrückt werden:
wie folgt ausgedrückt werden: 
Daraus kann die bedingte Verteilung des inversen Prozesses mithilfe der Bayes-Formel berechnet werden:

Allerdings handelt es sich bei der Verteilung um eine Mischung aus Gaußschen Verteilungen, die schwer in ein Netzwerk einzupassen ist. Daher gehen gängige Diffusionsmodelle normalerweise davon aus, dass diese Verteilung durch eine einzelne Gaußsche Verteilung angepasst werden kann.

wobei:  Um diese Hypothese zu testen, schätzt die Studie den Fehler dieser Anpassung in Satz 1.
Um diese Hypothese zu testen, schätzt die Studie den Fehler dieser Anpassung in Satz 1. 
Die Studie ergab jedoch, dass bei t=1, wenn s sich 1 nähert, auch  sich 1 nähert und der Fehler nicht ignoriert werden kann. Daher beweist Proposition 1 nicht die inverse Gaußsche Eigenschaft bei t=1. Um dieses Problem zu lösen, liefert diese Studie einen neuen Vorschlag:
sich 1 nähert und der Fehler nicht ignoriert werden kann. Daher beweist Proposition 1 nicht die inverse Gaußsche Eigenschaft bei t=1. Um dieses Problem zu lösen, liefert diese Studie einen neuen Vorschlag: 
Gemäß Satz 2 nähert sich  , wenn t=1 ist und s sich 1 nähert, 0. Somit beweist diese Studie, dass der gesamte inverse Prozess einschließlich des Singularitätsmoments den Gaußschen Eigenschaften entspricht. Sampling im Singularitätsmoment Betrachten Sie zunächst das Singularitätsproblem zum Zeitpunkt t=1. Wenn t=1, =0, wird der Nenner der folgenden Stichprobenformel durch 0 geteilt:
, wenn t=1 ist und s sich 1 nähert, 0. Somit beweist diese Studie, dass der gesamte inverse Prozess einschließlich des Singularitätsmoments den Gaußschen Eigenschaften entspricht. Sampling im Singularitätsmoment Betrachten Sie zunächst das Singularitätsproblem zum Zeitpunkt t=1. Wenn t=1, =0, wird der Nenner der folgenden Stichprobenformel durch 0 geteilt: Das Forschungsteam hat herausgefunden, dass durch die Berechnung des Grenzwerts der singuläre Punkt in einen trennbaren singulären Punkt umgewandelt werden kann:
Diese Grenze kann jedoch bei der Prüfung nicht berechnet werden. Zu diesem Zweck schlägt diese Studie vor, dass wir
zum Zeitpunkt t=1 anpassen und „x-Vorhersage“ verwenden können, um das Stichprobenproblem am anfänglichen singulären Punkt zu lösen. 

Betrachten Sie dann die Zeit t = 0. Der umgekehrte Prozess der Gaußschen Verteilungsanpassung wird zu einer Gaußschen Verteilung mit einer Varianz von 0, dh zur Dirac-Funktion:

wobei
. Solche Singularitäten führen dazu, dass der Stichprobenprozess zu den richtigen Daten konvergiert  . Daher ist die Singularität bei t=0 eine gute Eigenschaft des Diffusionsmodells und muss nicht vermieden werden. Darüber hinaus untersucht die Studie im Anhang auch das Singularitätsproblem in DDIM, SDE, ODE.
. Daher ist die Singularität bei t=0 eine gute Eigenschaft des Diffusionsmodells und muss nicht vermieden werden. Darüber hinaus untersucht die Studie im Anhang auch das Singularitätsproblem in DDIM, SDE, ODE. 
 Plug-and-Play-SingDiffusion-Modul
Plug-and-Play-SingDiffusion-Modul Die Abtastung an einzelnen Punkten wirkt sich auf die Qualität des vom Diffusionsmodell erzeugten Bildes aus. Wenn beispielsweise Hinweise mit hoher oder niedriger Helligkeit eingegeben werden, können bestehende Methoden oft nur Bilder mit durchschnittlichen Graustufen erzeugen, was als durchschnittliches Graustufenproblem bezeichnet wird. Dieses Problem ergibt sich aus der Tatsache, dass bestehende Methoden die Abtastung am singulären Punkt bei t=0 ignorieren und stattdessen die
Die Abtastung an einzelnen Punkten wirkt sich auf die Qualität des vom Diffusionsmodell erzeugten Bildes aus. Wenn beispielsweise Hinweise mit hoher oder niedriger Helligkeit eingegeben werden, können bestehende Methoden oft nur Bilder mit durchschnittlichen Graustufen erzeugen, was als durchschnittliches Graustufenproblem bezeichnet wird. Dieses Problem ergibt sich aus der Tatsache, dass bestehende Methoden die Abtastung am singulären Punkt bei t=0 ignorieren und stattdessen die Standard-Gauß-Verteilung
als Anfangsverteilung für die Abtastung zum Zeitpunkt 1-ϵ verwenden. Wie in der Abbildung oben gezeigt, besteht jedoch eine große Lücke zwischen der Standard-Gauß-Verteilung und der tatsächlichen Datenverteilung zum Zeitpunkt 1-ϵ.
Unter einer solchen Lücke entspricht die bestehende Methode gemäß Satz 3 der Erzeugung eines Bildes mit einem Mittelwert von 0 bei t = 1, also einem durchschnittlichen Graustufenbild. Daher ist es mit bestehenden Methoden schwierig, Bilder mit extrem starker oder schwacher Helligkeit zu erzeugen. Um dieses Problem zu lösen, schlägt diese Studie eine Plug-and-Play-SingDiffusion-Methode vor, um diese Lücke zu schließen, indem die Konvertierung zwischen einer Standard-Gauß-Verteilung und der tatsächlichen Datenverteilung angepasst wird. Der Algorithmus von SingDiffuion ist in der folgenden Abbildung dargestellt:

Gemäß der Schlussfolgerung des vorherigen Abschnitts verwendete diese Studie die „x-Prediction“-Methode zum Zeitpunkt t=1, um das Stichprobenproblem zu lösen am singulären Punkt. Für Bild-Text-Datenpaare  trainiert diese Methode ein Unet
trainiert diese Methode ein Unet  passend
passend  . Die Verlustfunktion wird wie folgt ausgedrückt:
. Die Verlustfunktion wird wie folgt ausgedrückt: 
Nachdem das Modell konvergiert ist, können Sie der folgenden DDIM-Abtastformel folgen und das neu erhaltene Modul  Abtastung
Abtastung verwenden.
verwenden. 
Die Abtastformel von DDIM stellt sicher, dass das generierte  der Datenverteilung
der Datenverteilung  zum 1-ε-Moment entspricht und löst so das durchschnittliche Graustufenproblem. Nach diesem Schritt kann das vorab trainierte Modell verwendet werden, um nachfolgende Stichprobenschritte durchzuführen, bis
zum 1-ε-Moment entspricht und löst so das durchschnittliche Graustufenproblem. Nach diesem Schritt kann das vorab trainierte Modell verwendet werden, um nachfolgende Stichprobenschritte durchzuführen, bis  generiert wird. Es ist erwähnenswert, dass SingDiffusion auf die meisten vorhandenen Diffusionsmodelle angewendet werden kann, da diese Methode nur am ersten Schritt der Probenahme beteiligt ist und nichts mit dem nachfolgenden Probenahmeprozess zu tun hat. Um das Datenüberlaufproblem zu vermeiden, das durch den Betrieb ohne Klassifikatorführung verursacht wird, verwendet diese Methode außerdem die folgende Normalisierungsoperation: Bei negativen Eingabeaufforderungen stellt pos die Ausgabe bei positiven Eingabeaufforderungen dar und ω stellt die Stärke der Führung dar.
generiert wird. Es ist erwähnenswert, dass SingDiffusion auf die meisten vorhandenen Diffusionsmodelle angewendet werden kann, da diese Methode nur am ersten Schritt der Probenahme beteiligt ist und nichts mit dem nachfolgenden Probenahmeprozess zu tun hat. Um das Datenüberlaufproblem zu vermeiden, das durch den Betrieb ohne Klassifikatorführung verursacht wird, verwendet diese Methode außerdem die folgende Normalisierungsoperation: Bei negativen Eingabeaufforderungen stellt pos die Ausgabe bei positiven Eingabeaufforderungen dar und ω stellt die Stärke der Führung dar. 
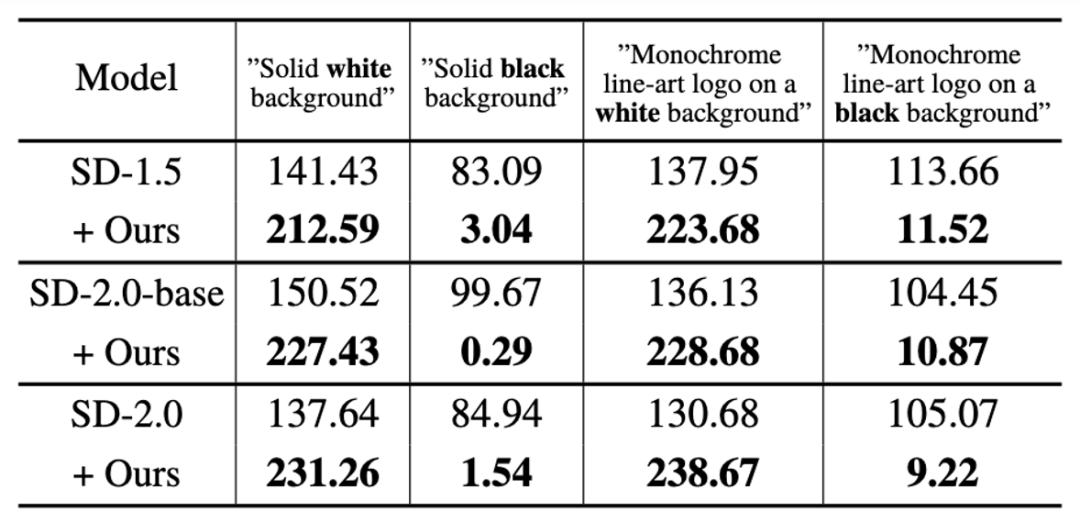
ExperimenteZuerst bestätigte diese Studie die Fähigkeit von SingDiffusion, das durchschnittliche Graustufenproblem auf drei Modellen zu lösen: SD-1.5, SD-2.0-Basis und SD-2.0. In dieser Studie wurden vier extreme Eingabeaufforderungen, darunter „reinweißer/schwarzer Hintergrund“ und „monochromes Strichzeichnungslogo auf weißem/schwarzem Hintergrund“, als Bedingungen für die Generierung ausgewählt und der durchschnittliche Graustufenwert des generierten Bildes berechnet, wie in der folgenden Tabelle gezeigt Angezeigt: Wie aus der Tabelle ersichtlich ist, kann diese Forschung das Problem des durchschnittlichen Grauwerts erheblich lösen und Bilder erzeugen, die der Helligkeit der Eingabetextbeschreibung entsprechen. Darüber hinaus visualisierte die Studie auch die Generierungsergebnisse unter diesen vier Eingabeaufforderungen, wie in der folgenden Abbildung dargestellt: 
Wie aus der Abbildung ersichtlich ist, kann das vorhandene Diffusionsmodell nach Hinzufügen dieser Methode Schwarz oder Weiß erzeugen Bild. 
Um die durch diese Methode erzielte Verbesserung der Bildqualität weiter zu untersuchen, wählte die Studie 30.000 Beschreibungen zum Testen im COCO-Datensatz aus. Erstens demonstriert diese Studie die generative Fähigkeit des Modells selbst, ohne eine klassifikatorfreie Anleitung zu verwenden, wie in der folgenden Tabelle gezeigt: Wie aus der Tabelle ersichtlich ist, kann die vorgeschlagene Methode den FID des generierten Modells erheblich reduzieren Bilder und verbessern CLIP-Anzeigen. Es ist erwähnenswert, dass die Methode in diesem Artikel im SD-1.5-Modell den FID-Index im Vergleich zum Originalmodell um 33 % reduziert. 
Um die Generierungsfähigkeit der vorgeschlagenen Methode ohne Klassifikatorführung zu überprüfen, zeigt die Studie außerdem in der folgenden Abbildung, dass unter verschiedenen Anleitungsgrößen ω∈[1,5,2,3,4,5,6, 7,8] Pareto-Kurve von CLIP vs. FID: Wie aus der Abbildung ersichtlich ist, kann die vorgeschlagene Methode auf derselben CLIP-Ebene niedrigere FID-Werte erzielen und realistischere Bilder erzeugen. Darüber hinaus demonstriert diese Studie auch die Generalisierungsfähigkeit der vorgeschlagenen Methode unter verschiedenen vorab trainierten CIVITAI-Modellen, wie in der folgenden Abbildung dargestellt: 
Es ist ersichtlich, dass die in dieser Studie vorgeschlagene Methode muss nur nach einem Training einfach auf vorhandene Diffusionsmodelle angewendet werden, um das Problem der durchschnittlichen Graustufen zu lösen.
Schließlich kann die in dieser Forschung vorgeschlagene Methode auch nahtlos auf das vorab trainierte ControlNet-Modell angewendet werden, wie in der folgenden Abbildung dargestellt: 
Wie aus den Ergebnissen ersichtlich ist, kann diese Methode den Durchschnitt effektiv lösen graues Problem des ControlNet-Gradproblems.
[1] Tero Karras, Miika Aittala, Timo Aila und Samuli Laine. Erläuterungen zum Designraum diffusionsbasierter generativer Modelle (NeurIPS), Seiten 26565–26577, 2022. 3Das obige ist der detaillierte Inhalt vonCVPR 2024|Kann bei extrem starkem Licht keine Bilder erzeugt werden? Das WeChat Vision Team löst effektiv das Singularitätsproblem des Diffusionsmodells. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Projektadresse: https://pangzecheung.github.io/SingDiffusion/
Projektadresse: https://pangzecheung.github.io/SingDiffusion/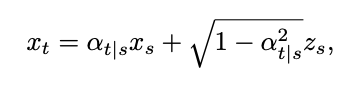
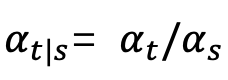 ,
, 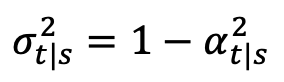 ,
, 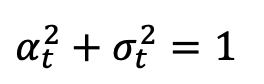 ,
, 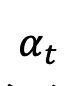 monoton mit sind Zeitwechsel von 1 auf 0. Unter Berücksichtigung der soeben definierten Trainingsmusterverteilung kann die Einzelmoment-Grenzwahrscheinlichkeitsdichte von
monoton mit sind Zeitwechsel von 1 auf 0. Unter Berücksichtigung der soeben definierten Trainingsmusterverteilung kann die Einzelmoment-Grenzwahrscheinlichkeitsdichte von 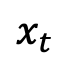 wie folgt ausgedrückt werden:
wie folgt ausgedrückt werden: 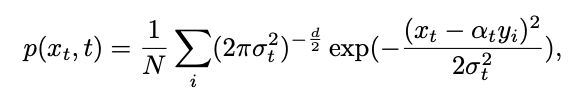
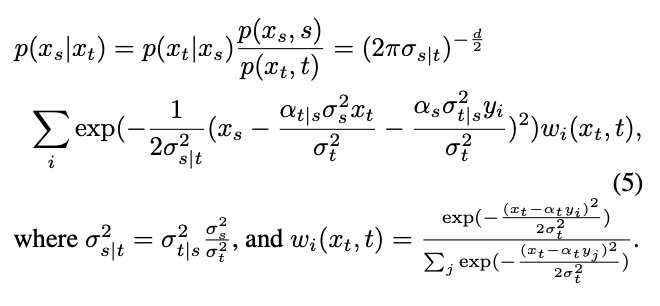
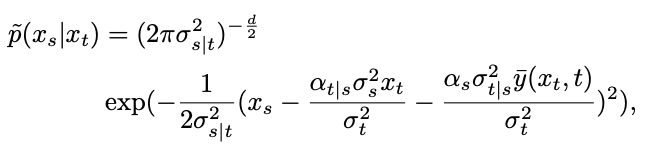
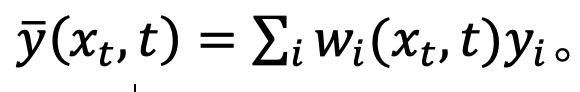 Um diese Hypothese zu testen, schätzt die Studie den Fehler dieser Anpassung in Satz 1.
Um diese Hypothese zu testen, schätzt die Studie den Fehler dieser Anpassung in Satz 1. 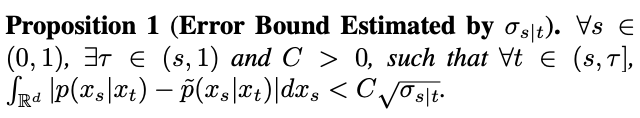
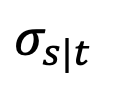 sich 1 nähert und der Fehler nicht ignoriert werden kann. Daher beweist Proposition 1 nicht die inverse Gaußsche Eigenschaft bei t=1. Um dieses Problem zu lösen, liefert diese Studie einen neuen Vorschlag:
sich 1 nähert und der Fehler nicht ignoriert werden kann. Daher beweist Proposition 1 nicht die inverse Gaußsche Eigenschaft bei t=1. Um dieses Problem zu lösen, liefert diese Studie einen neuen Vorschlag: 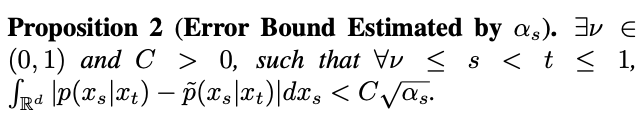
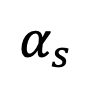 , wenn t=1 ist und s sich 1 nähert, 0. Somit beweist diese Studie, dass der gesamte inverse Prozess einschließlich des Singularitätsmoments den Gaußschen Eigenschaften entspricht. Sampling im Singularitätsmoment
, wenn t=1 ist und s sich 1 nähert, 0. Somit beweist diese Studie, dass der gesamte inverse Prozess einschließlich des Singularitätsmoments den Gaußschen Eigenschaften entspricht. Sampling im Singularitätsmoment 
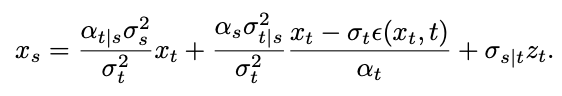
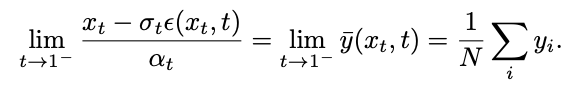
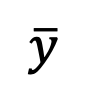 . Daher ist die Singularität bei t=0 eine gute Eigenschaft des Diffusionsmodells und muss nicht vermieden werden.
. Daher ist die Singularität bei t=0 eine gute Eigenschaft des Diffusionsmodells und muss nicht vermieden werden. 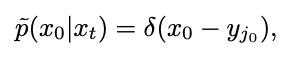
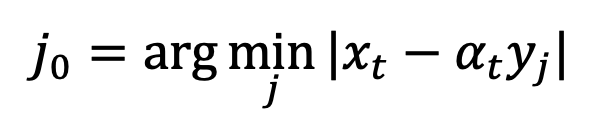 Plug-and-Play-SingDiffusion-Modul
Plug-and-Play-SingDiffusion-Modul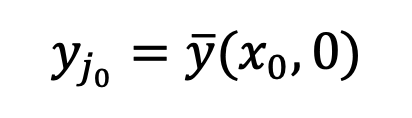

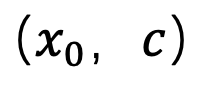 trainiert diese Methode ein Unet
trainiert diese Methode ein Unet 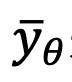 passend
passend 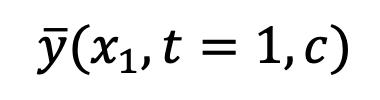 . Die Verlustfunktion wird wie folgt ausgedrückt:
. Die Verlustfunktion wird wie folgt ausgedrückt: 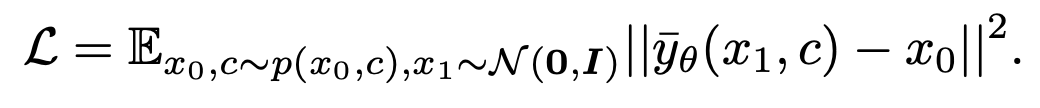
 Abtastung
Abtastung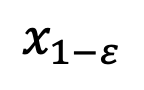 verwenden.
verwenden. 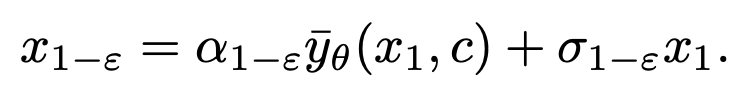
 der Datenverteilung
der Datenverteilung 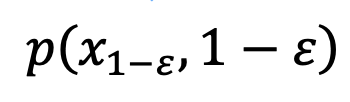 zum 1-ε-Moment entspricht und löst so das durchschnittliche Graustufenproblem. Nach diesem Schritt kann das vorab trainierte Modell verwendet werden, um nachfolgende Stichprobenschritte durchzuführen, bis
zum 1-ε-Moment entspricht und löst so das durchschnittliche Graustufenproblem. Nach diesem Schritt kann das vorab trainierte Modell verwendet werden, um nachfolgende Stichprobenschritte durchzuführen, bis 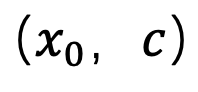 generiert wird. Es ist erwähnenswert, dass SingDiffusion auf die meisten vorhandenen Diffusionsmodelle angewendet werden kann, da diese Methode nur am ersten Schritt der Probenahme beteiligt ist und nichts mit dem nachfolgenden Probenahmeprozess zu tun hat. Um das Datenüberlaufproblem zu vermeiden, das durch den Betrieb ohne Klassifikatorführung verursacht wird, verwendet diese Methode außerdem die folgende Normalisierungsoperation: Bei negativen Eingabeaufforderungen stellt pos die Ausgabe bei positiven Eingabeaufforderungen dar und ω stellt die Stärke der Führung dar.
generiert wird. Es ist erwähnenswert, dass SingDiffusion auf die meisten vorhandenen Diffusionsmodelle angewendet werden kann, da diese Methode nur am ersten Schritt der Probenahme beteiligt ist und nichts mit dem nachfolgenden Probenahmeprozess zu tun hat. Um das Datenüberlaufproblem zu vermeiden, das durch den Betrieb ohne Klassifikatorführung verursacht wird, verwendet diese Methode außerdem die folgende Normalisierungsoperation: Bei negativen Eingabeaufforderungen stellt pos die Ausgabe bei positiven Eingabeaufforderungen dar und ω stellt die Stärke der Führung dar.