 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte KI
KI Lernen Sie gut lineare Algebra und spielen Sie mit Empfehlungssystemen
Lernen Sie gut lineare Algebra und spielen Sie mit EmpfehlungssystemenLernen Sie gut lineare Algebra und spielen Sie mit Empfehlungssystemen
Autor |. Wang Hao
Rezensent |. Apropos 21
Century Internet-Technologie, außerPython/Rust/Go Warten Sie eine Minute Die Geburt Ein Highlight sind auch die Entwicklung einer Reihe neuer Programmiersprachen und die starke Entwicklung der Information-Retrieval-Technologie. Das erste rein technologische Geschäftsmodell im Internet war die Suchmaschinentechnologie, vertreten durch Google und Baidu. Was jedoch nicht jeder erwartet, ist, dass das Empfehlungssystem schon vor langer Zeit geboren wurde. Bereits 1992 wurde das erste Empfehlungssystem in der Geschichte der Menschheit in Form eines Papiers veröffentlicht. Zu diesem Zeitpunkt waren Google und Baidu noch nicht geboren. wird nicht als starre Notwendigkeit betrachtet wie Suchmaschinen, und viele Einhörner wurden bald geboren. Technologieunternehmen mit Empfehlungssystemen als Kerntechnologie werden erst mit dem Aufstieg von Toutiao und Douyin in der Ära
2010 
—— Informationsabruf basierend auf großen Sprachmodellen. Derzeit sind europäische und amerikanische Länder die Vorreiter, aber China und die Vereinigten Staaten gehen derzeit gemeinsam voran. In den letzten Jahren hat die maßgebliche Konferenz auf dem Gebiet der Empfehlungssysteme RecSys
häufig den Preis für das beste Papier anSequential Recommendation (Sequential Recommendation) verliehen. Dies zeigt, dass in diesem Bereich vertikale Anwendungen immer mehr Beachtung finden. Es gibt eine vertikale Anwendung des Empfehlungssystems, die so wichtig ist, aber bisher keine großen Wellen geschlagen hat. In diesem Bereich handelt es sich um szenariobasierte Empfehlungen (Kontextbewusste Empfehlung), die als CARS bezeichnet werden. Gelegentlich sehen wir einige WORKSHOP von CARS , aber diese Workshop produzieren jedes Jahr nicht mehr als 10 Papiere, was eine Handvoll ist. AUTOS Wofür kann es verwendet werden? Erstens wird
CARSbereits von Fast-Food-Unternehmen wie Burger King genutzt. Es kann Benutzern auch Musik basierend auf der Szene während der Autofahrt empfehlen. Darüber hinaus können wir darüber nachdenken, ob es uns möglich ist, Benutzern Reisepläne basierend auf den Wetterbedingungen zu empfehlen. Oder Benutzern Mahlzeiten basierend auf ihrer körperlichen Verfassung empfehlen? Solange wir unserer Fantasie freien Lauf lassen, können wir tatsächlich immer verschiedene praktische Anwendungen für AUTOS finden. Es stellt sich jedoch die Frage: Da CARS
so weit verbreitet ist, warum veröffentlichen so wenige Menschen Artikel? Der Grund ist einfach, denn fürCARS sind fast keine öffentlichen Datensätze verfügbar. Der derzeit beste öffentliche Datensatz von CARS ist der LDOS-CoMoDa Datensatz aus Slowenien. Abgesehen davon ist es schwierig, andere Datensätze zu finden. LDOS-CoMoDa stellt Benutzerszenendaten beim Ansehen von Filmen in Form von Umfragen bereit und ermöglicht es Forschern, sich an der CARS -Forschung zu beteiligen. Der Zeitpunkt für die Offenlegung der Daten liegt zwischen 2012 und 2013 , aber derzeit wissen nur sehr wenige Menschen von dieser Datenerhebung. Zurück zur Sache: In diesem Artikel werden hauptsächlich der Algorithmus MatMat / MovieMat
und der AlgorithmusPowerMat vorgestellt. Diese Algorithmen sind leistungsstarke Werkzeuge zur Lösung des CARS -Problems. Schauen wir uns zunächst an, wie MatMat das CARS -Problem definiert: Wir definieren zunächst die Benutzerbewertungsmatrix neu und ersetzen jeden Bewertungswert der Benutzerbewertungsmatrix durch eine quadratische Matrix. Die diagonalen Elemente der quadratischen Matrix sind die ursprünglichen Bewertungswerte und die nicht diagonalen Elemente sind Szeneninformationen. Im Folgenden definieren wir die Verlustfunktion des
MatMat 
wobei U und V beide Matrizen sind. Auf diese Weise ändern wir das Vektorskalarprodukt in der ursprünglichen Matrixfaktorisierung. Verwandeln Sie die Vektorpunktmultiplikation in eine Matrixmultiplikation. Nehmen wir das folgende Beispiel:
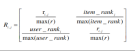
Wir haben ein Leistungsvergleichsexperiment mit MovieLens Small Dataset durchgeführt und die folgenden Ergebnisse erhalten:

Wie Sie sehen können, MatMa t Die Wirkung des Algorithmus ist besser als die des klassischen Matrixzerlegungsalgorithmus. Überprüfen wir noch einmal die Fairness des Empfehlungssystems:

Es zeigt sich, dass MatMat in Bezug auf Fairness-Indikatoren immer noch gut abschneidet. Der Lösungsprozess von MatMat ist relativ kompliziert. Selbst der Autor, der den Algorithmus erfunden hat, hat den Ableitungsprozess nicht in der Arbeit beschrieben. Aber wie heißt es so schön: Wenn Sie lineare Algebra lernen, werden Sie keine Angst davor haben, um die ganze Welt zu reisen. Ich glaube, dass kluge Leser in der Lage sein werden, die relevanten Formeln abzuleiten und diesen Algorithmus zu implementieren. MatMat Die Originaladresse des Algorithmuspapiers finden Sie unter folgendem Link: https://www.php.cn/link/9b8c60725a0193e78368bf8b84c37fb2 . Dieses Papier ist der Best Paper Report Award der International Academic Conference IEEE ICISCAE 2021 . Der Algorithmus
MatMat wird im Bereich der szenenbasierten Filmempfehlung angewendet. Die Filminstanz dieses Algorithmus heißt MovieMat. Die Bewertungsmatrix von MovieMat ist wie folgt definiert:
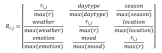
Der Autor führte dann ein Vergleichsexperiment durch:

auf dem LDOS-CoMoDa Datensatz, MovieMat erreicht eine weitaus höhere Leistung als die klassische Matrixzerlegung. Werfen wir einen Blick auf die Ergebnisse der Fairness-Bewertung:

In Bezug auf Fairness hat die klassische Matrixzerlegung bessere Ergebnisse erzielt als MovieMat . Das Originalpapier von MovieMat finden Sie unter folgendem Link: https://www.php.cn/link/f4ec6380c50a68a7c35d109bec48aebf .
Manchmal stoßen wir auf solche Probleme. Was sollen wir tun, wenn wir an einem neuen Ort ankommen und nur Szenendaten, aber keine Benutzerbewertungsdaten haben? Es spielt keine Rolle, Ratidar Technologies LLC (Beijing Daping Qizhi Network Technology Co., Ltd. ) hat den Algorithmus CARS basierend auf Zero-Shot-Lernen erfunden – PowerMat. Das Originalpapier von PowerMat finden Sie unter folgendem Link: https://www.php.cn/link/1514f187930072575629709336826443 . Der Erfinder von
PowerMat hat sich MAP und DotMat ausgeliehen und die folgende MAP -Funktion definiert:

wo U ist der Benutzer The Feature-Vektor, V ist der Element-Feature-Vektor, R ist der Benutzerbewertungswert und C ist die Szenenvariable. Konkret erhalten wir die folgende Formel:

Durch die Verwendung des stochastischen Gradientenabstiegs zur Lösung dieses Problems erhalten wir die folgende Formel:
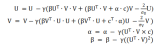
Durch Beobachtung haben wir festgestellt, dass dieser Formelsatz keine eingabedatenbezogenen Variablen enthält, also PowerMat ist ein Zero-Shot-Lernalgorithmus, der sich nur auf Szenarien bezieht. Dieser Algorithmus kann in den folgenden Szenarien angewendet werden: Touristen planen eine Reise zu einem bestimmten Ort, waren aber noch nie dort und verfügen daher nur über Szenendaten wie das Wetter. Wir können PowerMat verwenden, um Check-in-Attraktionen zu empfehlen Touristen usw.
Das Folgende sind die Vergleichsdaten zwischen PowerMat und anderen Algorithmen:

Durch dieses Bild finden wir PowerMat und MovieMat Flagge Die Trommeln sind ruhig, nicht Sie sind vergleichbar und die Ergebnisse sind besser als der klassische Matrixzerlegungsalgorithmus. Das Bild unten zeigt, dass PowerMat auch im Hinblick auf den Fairness--Index immer noch eine starke Leistung erbringt:

Durch Vergleichsexperimente haben wir festgestellt, dass PowerMat ausgezeichnet ist AUTOS Algorithmus.
Internet-Dateningenieure sagen oft, dass Daten über allem anderen stehen. Und um die Ära 2010 gab es im Internet einen starken Trend, der bei Daten optimistisch und bei Algorithmen bärisch war. CARS ist ein tolles Beispiel. Da die überwiegende Mehrheit der Menschen keinen Zugriff auf relevante Daten hat, ist die Entwicklung dieses Bereichs stark eingeschränkt. Dank slowenischer Forscher für die Veröffentlichung der LDOS-CoMoDa Datensammlung haben wir die Möglichkeit, dieses Feld weiterzuentwickeln. Wir hoffen auch, dass immer mehr Menschen auf Autos, die Landung von Autos und die Finanzierung von Autos ... achten
Funplus Leiter des Labors für künstliche Intelligenz. Er hatte Technologie- und Technologieführungspositionen bei
Das obige ist der detaillierte Inhalt vonLernen Sie gut lineare Algebra und spielen Sie mit Empfehlungssystemen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Teslas Robovan war das versteckte Juwel im Robotaxi -Teaser 2024Apr 22, 2025 am 11:48 AM
Teslas Robovan war das versteckte Juwel im Robotaxi -Teaser 2024Apr 22, 2025 am 11:48 AMSeit 2008 habe ich mich für den Shared-Bride-Van eingesetzt, der als "Robotjitney" als "Vansit" als Zukunft des städtischen Transports bezeichnet wurde. Ich sehe diese Fahrzeuge als Transitlösung der nächsten Generation des 21. Jahrhunderts, Surpas, voraus
 Sam's Club -Wetten auf KI zur Beseitigung von Quittungsprüfungen und zur Verbesserung des EinzelhandelsApr 22, 2025 am 11:29 AM
Sam's Club -Wetten auf KI zur Beseitigung von Quittungsprüfungen und zur Verbesserung des EinzelhandelsApr 22, 2025 am 11:29 AMRevolutionieren die Erfahrung im Checkout Der innovative "Just Go" -System von Sam's Club baut auf seiner vorhandenen KI-angetriebenen "Scan & Go" -Technologie auf und ermöglicht es den Mitgliedern, während ihres Einkaufsbaus Einkäufe über die Sam's Club-App zu scannen.
 Die AI -Omniverse von Nvidia erweitert sich bei GTC 2025Apr 22, 2025 am 11:28 AM
Die AI -Omniverse von Nvidia erweitert sich bei GTC 2025Apr 22, 2025 am 11:28 AMVerbesserte Vorhersehbarkeit und neue Produktaufstellung von NVIDIA bei GTC 2025 Nvidia, ein wichtiger Akteur in der KI -Infrastruktur, konzentriert sich auf eine erhöhte Vorhersagbarkeit seiner Kunden. Dies beinhaltet eine konsequente Produktlieferung, die Erwartung der Leistungsverwaltung und die Erfüllung der Leistungsverwalter und beinhaltet
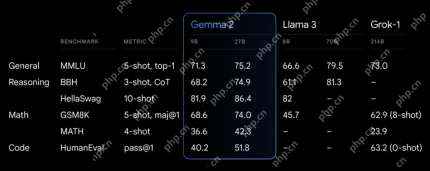 Erkundung der Funktionen der Gemma 2 -Modelle von Google.Apr 22, 2025 am 11:26 AM
Erkundung der Funktionen der Gemma 2 -Modelle von Google.Apr 22, 2025 am 11:26 AMGoogles Gemma 2: Ein leistungsstarkes, effizientes Sprachmodell Die Gemma-Familie von Google von Sprachmodellen, die für Effizienz und Leistung gefeiert wurde
 Die nächste Welle von Genai: Perspektiven mit Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AM
Die nächste Welle von Genai: Perspektiven mit Dr. Kirk Borne - Analytics VidhyaApr 22, 2025 am 11:21 AMDiese Führung mit Daten -Episode zeigt Dr. Kirk Borne, einen führenden Datenwissenschaftler, Astrophysiker und TEDX -Sprecher. Dr. Borne, ein renommierter Experte für Big Data, KI und maschinelles Lernen, bietet unschätzbare Einblicke in den aktuellen Zustand und den zukünftigen Traje
 KI für Läufer und Sportler: Wir machen hervorragende FortschritteApr 22, 2025 am 11:12 AM
KI für Läufer und Sportler: Wir machen hervorragende FortschritteApr 22, 2025 am 11:12 AMEs gab einige sehr aufschlussreiche Perspektiven in dieser Rede - Background -Informationen über Ingenieurwesen, die uns zeigten, warum künstliche Intelligenz so gut darin ist, die körperliche Bewegung der Menschen zu unterstützen. Ich werde eine Kernidee aus der Perspektive jedes Mitwirkenden skizzieren, um drei Designaspekte zu demonstrieren, die ein wichtiger Bestandteil unserer Erforschung der Anwendung künstlicher Intelligenz im Sport sind. Edge -Geräte und rohe personenbezogene Daten Diese Vorstellung von künstlicher Intelligenz enthält tatsächlich zwei Komponenten - eine, die sich darauf bezieht, wo wir große Sprachmodelle platzieren, und die andere hängt mit den Unterschieden zwischen unserer menschlichen Sprache und der Sprache zusammen, die unsere Vitalfunktionen „ausdrücken“, wenn sie in Echtzeit gemessen werden. Alexander Amini weiß viel über Laufen und Tennis, aber er immer noch
 Jamie Engstrom über Technologie, Talent und Transformation bei CaterpillarApr 22, 2025 am 11:10 AM
Jamie Engstrom über Technologie, Talent und Transformation bei CaterpillarApr 22, 2025 am 11:10 AMJamie Engstrom, Chief Information Officer und Senior Vice President It, leitet ein globales Team von über 2.200 IT -Fachleuten in 28 Ländern. Mit 26 Jahren in Caterpillar, darunter viereinhalb Jahre in ihrer gegenwärtigen Rolle, Engst
 Neues Google -Fotos Update macht ein Foto mit Ultra HDR -Qualität PopApr 22, 2025 am 11:09 AM
Neues Google -Fotos Update macht ein Foto mit Ultra HDR -Qualität PopApr 22, 2025 am 11:09 AMDas neue Ultra HDR -Tool von Google Photos: Eine schnelle Anleitung Verbessern Sie Ihre Fotos mit dem neuen Ultra HDR-Tool von Google Photos und verwandeln Sie Standardbilder in lebendige Meisterwerke mit hohem Dynamik. Dieses Tool ist ideal für soziale Medien und steigert die Auswirkungen eines Fotos.


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Herunterladen der Mac-Version des Atom-Editors
Der beliebteste Open-Source-Editor

SublimeText3 Linux neue Version
SublimeText3 Linux neueste Version

mPDF
mPDF ist eine PHP-Bibliothek, die PDF-Dateien aus UTF-8-codiertem HTML generieren kann. Der ursprüngliche Autor, Ian Back, hat mPDF geschrieben, um PDF-Dateien „on the fly“ von seiner Website auszugeben und verschiedene Sprachen zu verarbeiten. Es ist langsamer und erzeugt bei der Verwendung von Unicode-Schriftarten größere Dateien als Originalskripte wie HTML2FPDF, unterstützt aber CSS-Stile usw. und verfügt über viele Verbesserungen. Unterstützt fast alle Sprachen, einschließlich RTL (Arabisch und Hebräisch) und CJK (Chinesisch, Japanisch und Koreanisch). Unterstützt verschachtelte Elemente auf Blockebene (wie P, DIV),

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

SecLists
SecLists ist der ultimative Begleiter für Sicherheitstester. Dabei handelt es sich um eine Sammlung verschiedener Arten von Listen, die häufig bei Sicherheitsbewertungen verwendet werden, an einem Ort. SecLists trägt dazu bei, Sicherheitstests effizienter und produktiver zu gestalten, indem es bequem alle Listen bereitstellt, die ein Sicherheitstester benötigen könnte. Zu den Listentypen gehören Benutzernamen, Passwörter, URLs, Fuzzing-Payloads, Muster für vertrauliche Daten, Web-Shells und mehr. Der Tester kann dieses Repository einfach auf einen neuen Testcomputer übertragen und hat dann Zugriff auf alle Arten von Listen, die er benötigt.




