Datenstrukturen und Algorithmen in JavaScript (3): verknüpfte list_javascript-Kenntnisse

Wir können sehen, dass die Warteschlange und der Stapel im JavaScript-Konzept sowohl eine spezielle lineare Listenstruktur als auch eine relativ einfache Array-basierte sequentielle Speicherstruktur sind. Da der JavaScript-Interpreter direkt für Arrays optimiert wurde, gibt es in vielen Programmiersprachen nicht das Problem der festen Länge von Arrays (es ist schwieriger, das Array hinzuzufügen, nachdem es voll ist, einschließlich Hinzufügen und Löschen, alles muss sein). im Array) Alle Elemente ändern ihre Position, und JavaScript-Arrays werden tatsächlich direkt optimiert, z. B. Push-, Pop-, Shift-, Unshift-, Split-Methoden usw.)

Der größte Nachteil der sequentiellen Speicherstruktur einer linearen Tabelle besteht darin, dass die Änderung der Anordnung eines der Elemente zu Änderungen in der gesamten Sammlung führt. Der Grund dafür ist, dass die Speicherung im Speicher von Natur aus kohärent ist und keine Lücken aufweist. Das Löschen eines Elements wird dies natürlich ausgleichen. Nach der Optimierung dieser Struktur ist die Kettenspeicherstruktur entstanden. Um die Denkweise zu ändern, ist uns die Anordnung der Daten völlig egal. Wir müssen also nur die Position der nächsten Daten innerhalb jedes Elements aufzeichnen Verwendung Die im Link-Modus gespeicherte lineare Liste wird kurz als verknüpfte Liste bezeichnet. In der verknüpften Struktur lautet data = (Informationsadresse)

In der Kettenstruktur können wir die Adresse auch als „Kette“ bezeichnen. Eine Dateneinheit ist ein Knoten, sodass man sagen kann, dass die verknüpfte Liste eine Sammlung von Knoten ist. Jeder Knoten verfügt über eine Datenblockreferenz, die auf seinen nächsten Knoten

verweist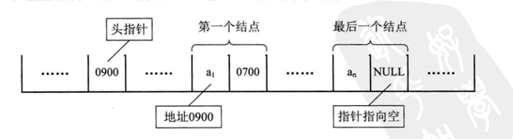

Array-Elemente werden basierend auf Positionsbeziehungen logisch referenziert, während verknüpfte Listen basierend darauf referenziert werden, dass jedes Datenelement eine Referenzzeigerbeziehung speichert

Die Vorteile dieser Struktur liegen auf der Hand. Beim Einfügen eines Datenelements müssen Sie sich überhaupt keine Gedanken über dessen Anordnung machen. Sie müssen lediglich die Richtungen der „Kette“ verbinden

Die Idee verknüpfter Listen ist auf diese Weise nicht auf Arrays beschränkt. Wir können Objekte verwenden, solange eine Referenzbeziehung zwischen Objekten besteht

Leads umfassen im Allgemeinen einfach verknüpfte Listen, statisch verknüpfte Listen, zirkulär verknüpfte Listen und doppelt verknüpfte Listen

Einfach verknüpfte Liste: Es handelt sich um eine sehr einfache Abwärtsübertragung. Genau wie Tony Leung in Infernal Affairs kommuniziert der Undercover-Agent mit dem Vermittler wird abgeschnitten, dann kann ich meine Identität nicht beweisen, daher steht am Ende des Films ein Satz: „Ich bin ein guter Mensch, wer weiß?“

Statische verknüpfte Liste: Es handelt sich um eine verknüpfte Liste, die durch ein Array beschrieben wird. Das heißt, jede Tabelle im Array ist ein „Abschnitt“, der Daten und Zeiger

enthält

Zirkular verknüpfte Liste: Da die einfach verknüpfte Liste nur rückwärts weitergegeben wird, ist es beim Erreichen des Endes sehr mühsam, zum Kopf zurückzukehren, sodass die Kette des Endabschnitts mit dem Kopf verbunden wird, um eine zu bilden Schleife

Doppelt verknüpfte Liste: Optimierung für einfach verknüpfte Listen, sodass jeder Abschnitt wissen kann, wer davor und danach ist. Daher wird es zusätzlich zum hinteren Zeigerfeld auch ein vorderes Zeigerfeld geben, was die Sucheffizienz verbessert, aber bringt einige Designprobleme mit sich. Im Allgemeinen besteht die Komplexität darin, Raum gegen Zeit auszutauschen

Zusammenfassend lässt sich sagen, dass die verknüpfte Liste tatsächlich eine Optimierungsmethode für die sequentielle Speicherstruktur in der linearen Liste ist. Aufgrund der Besonderheit des Arrays (automatische Aktualisierung der Referenzposition) haben wir jedoch kann Objekte zum Speichern der verknüpften Liste verwenden

Einfach verknüpfte Liste

Wir implementieren die einfachste verknüpfte Listenbeziehung

function createLinkList() {
  var _this = {},
    prev = null;
  return {
    add: function(val) {
      //保存当前的引用
      prev = {
        data: val,
        next: prev || null
      }
    }
  }
}
var linksList = createLinkList(); 
linksList.add("arron1"); 
linksList.add("arron2"); 
linksList.add("arron3");
//node节的next链就是 -arron3-arron2-arron1

Verweisen Sie direkt auf das nächste Knotenobjekt über das nächste Knotenobjekt. Diese Kettenidee wird zunächst in der then-Methode in der asynchronen Verzögerung von jQuery und in der jsderferre von Japans cho45 verwendet . . Bei dieser Implementierung gibt es noch ein weiteres äußerst kritisches Problem: Wie fügen wir Daten dynamisch nach dem ausgeführten Abschnitt ein?

Wir müssen also eine Traversal-Methode entwerfen, um die Daten in dieser Knotenkette zu durchsuchen, dann die entsprechenden Daten finden, den neuen Abschnitt in die aktuelle Kette einfügen und den Standortdatensatz neu schreiben

//在链表中找到对应的节
var findNode = function createFindNode(currNode) {
  return function(key){
    //循环找到执行的节，如果没有返回本身
    while (currNode.data != key) {
      currNode = currNode.next;
    }
    return currNode;        
  }
}(headNode);

Dies ist eine Methode zum Suchen des aktuellen Abschnitts, indem der ursprüngliche Head-HeadNode-Abschnitt übergeben wird, um als nächstes zu suchen, bis die entsprechenden Abschnittsinformationen gefunden werden

Dies wird mit der Curry-Methode umgesetzt

Beim Einfügen eines Abschnitts lautet die Konvertierungsbeziehung für die Adresse der verknüpften Liste wie folgt:

Wenn Sie in der verknüpften Liste von a-b-c-d ein f

nach c(c.next->d) einfügen möchten

a-b-c-f-d , dann c,next->f , f.next-d

Abschnitt über die Einfügemethode hinzufügen

首先分离出createNode节的构建，在初始化的时候先创建一个头部节对象用来做节开头的初始化对象

在insert增加节方法中，通过对headNode链的一个查找，找到对应的节，把新的节给加后之后，最后就是修改一下链的关系

如何从链表中删除一个节点？

由于链表的特殊性，我们a->b->c->d  ，如果要删除c那么就必须修改b.next->c为 b.next->d，所以找到前一个节修改其链表next地址，这个有点像dom操作中removeChild找到其父节点调用移除子节点

同样的我们也在remove方法的设计中，需要设计一个遍历往上回溯一个父节点即可

//找到前一个节
var findPrevious = function(currNode) {
  return function(key){
    while (!(currNode.next == null) &&
      (currNode.next.data != key)) {
      currNode = currNode.next;
    }
    return currNode;      
  }
}(headNode);

//插入方法
this.remove = function(key) {
  var prevNode = findPrevious(key);
  if (!(prevNode.next == null)) {
    //修改链表关系
    prevNode.next = prevNode.next.next;
  }
};

测试代码：

<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">
 //////////
 //创建链表 //
 //////////
 function createLinkList() {

 //创建节
 function createNode(data) {
  this.data = data;
  this.next = null;
 }

 //初始化头部节
 //从headNode开始形成一条链条
 //通过next衔接
 var headNode = new createNode("head");

 //在链表中找到对应的节
 var findNode = function createFindNode(currNode) {
  return function(key) {
  //循环找到执行的节，如果没有返回本身
  while (currNode.data != key) {
   currNode = currNode.next;
  }
  return currNode;
  }
 }(headNode);

 //找到前一个节
 var findPrevious = function(currNode) {
  return function(key) {
  while (!(currNode.next == null) &&
   (currNode.next.data != key)) {
   currNode = currNode.next;
  }
  return currNode;
  }
 }(headNode);


 //插入一个新节
 this.insert = function(data, key) {
  //创建一个新节
  var newNode = new createNode(data);
  //在链条中找到对应的数据节
  //然后把新加入的挂进去
  var current = findNode(key);
  //插入新的接，更改引用关系
  //1:a-b-c-d
  //2:a-b-n-c-d
  newNode.next = current.next;
  current.next = newNode;
 };

 //插入方法
 this.remove = function(key) {
  var prevNode = findPrevious(key);
  if (!(prevNode.next == null)) {
  //修改链表关系
  prevNode.next = prevNode.next.next;
  }
 };


 this.display = function(fn) {
  var currNode = headNode;
  while (!(currNode.next == null)) {
  currNode = currNode.next;
  fn(currNode.data)
  }
 };

 }


 var cities = new createLinkList();

 function create() {
 var text = '';
 cities.display(function(data) {
  text += '-' + data;
 });
 var div = document.createElement('div')
 div.innerHTML = text;
 document.getElementById("listshow").appendChild(div)
 }

 document.getElementById("test1").onclick = function() {
 cities.insert("Conway", "head");
 cities.insert("Russellville", "Conway");
 cities.insert("Carlisle", "Russellville");
 cities.insert("Alma", "Carlisle");
 create();
 }

 document.getElementById("test2").onclick = function() {
 cities.remove("Russellville");
 create()
 }

</script>

双链表

原理跟单链表是一样的，无非就是给每一个节增加一个前链表的指针

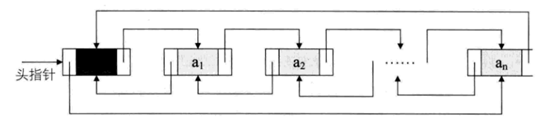
增加节

//插入一个新节
this.insert = function(data, key) {
  //创建一个新节
  var newNode = new createNode(data);
  //在链条中找到对应的数据节
  //然后把新加入的挂进去
  var current = findNode(headNode,key);
  //插入新的接，更改引用关系
  newNode.next   = current.next;
  newNode.previous = current
  current.next   = newNode;
};

删除节

this.remove = function(key) {
  var currNode = findNode(headNode,key);
  if (!(currNode.next == null)) {
    currNode.previous.next = currNode.next;
    currNode.next.previous = currNode.previous;
    currNode.next     = null;
    currNode.previous   = null;
  }
};

在删除操作中有一个明显的优化：不需要找到父节了，因为双链表的双向引用所以效率比单链要高

测试代码：

<!doctype html><button id="test1">插入多条数据</button>
<button id="test2">删除Russellville数据</button><div id="listshow"><br /></div><script type="text/javascript">

 //////////
 //创建链表 //
 //////////
 function createLinkList() {

 //创建节
 function createNode(data) {
  this.data = data;
  this.next = null;
  this.previous = null
 }

   //初始化头部节
 //从headNode开始形成一条链条
 //通过next衔接
 var headNode = new createNode("head");

 //在链表中找到对应的数据
 var findNode = function(currNode, key) {
  //循环找到执行的节，如果没有返回本身
  while (currNode.data != key) {
  currNode = currNode.next;
  }
  return currNode;
 }

 //插入一个新节
 this.insert = function(data, key) {
  //创建一个新节
  var newNode = new createNode(data);
  //在链条中找到对应的数据节
  //然后把新加入的挂进去
  var current = findNode(headNode,key);
  //插入新的接，更改引用关系
  newNode.next   = current.next;
  newNode.previous = current
  current.next   = newNode;
 };

 this.remove = function(key) {
  var currNode = findNode(headNode,key);
  if (!(currNode.next == null)) {
  currNode.previous.next = currNode.next;
  currNode.next.previous = currNode.previous;
  currNode.next     = null;
  currNode.previous   = null;
  }
 };

 this.display = function(fn) {
  var currNode = headNode;
  while (!(currNode.next == null)) {
  currNode = currNode.next;
  fn(currNode.data)
  }
 };

 }


 var cities = new createLinkList();

 function create() {
 var text = '';
 cities.display(function(data) {
  text += '-' + data;
 });
 var div = document.createElement('div')
 div.innerHTML = text;
 document.getElementById("listshow").appendChild(div)
 }

 document.getElementById("test1").onclick = function() {
 cities.insert("Conway", "head");
 cities.insert("Russellville", "Conway");
 cities.insert("Carlisle", "Russellville");
 cities.insert("Alma", "Carlisle");
 create();
 }

 document.getElementById("test2").onclick = function() {
 cities.remove("Russellville");
 create()
 }


</script>

git代码下载：https://github.com/JsAaron/data_structure.git