Datenstrukturen und Algorithmen in JavaScript (1): Stack_Javascript-Kenntnisse

Vorwort

Datenstrukturen und Algorithmen JavaScript ist ein Buch, das es auf relativ einfache Weise erklärt. Der Vorteil besteht darin, dass es die JavaScript-Sprache verwendet, um häufig verwendete Datenstrukturen zu beschreiben, die berücksichtigt werden können Um mit der Zeit zu gehen, habe ich es mir als Amateur angeschaut und nebenbei aufgenommen

Git-Code-Download: https://github.com/JsAaron/data_structure.git

Stapelstruktur

Spezielle Liste, auf die Elemente im Stapel kann nur über ein Ende der Liste, die Oberseite des Stapels, zugegriffen werden

Last-in-first-out (LIFO, last-in-first-out) Datenstruktur

Javascript bietet ausführbare Methoden, Push und Pop, aber Pop entfernt die Daten im Stapel

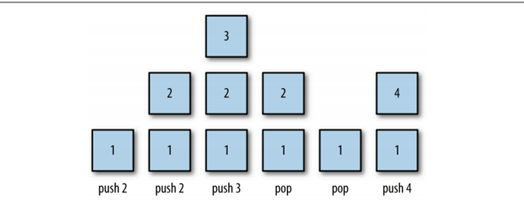
Eine Implementierungsklasse, die einen Stapel implementiert

Die zugrunde liegende Datenstruktur verwendet Arrays

Da pop die Daten im Stapel löscht, müssen Sie eine Suchmethode peek implementieren

Implementieren Sie eine klare Reinigungsmethode

Ermitteln Sie die Gesamtzahl der Elemente in der Stapellänge

Überprüfen Sie, ob das Element noch leer ist

Code kopieren Der Code lautet wie folgt:

Funktion Stack(){
This.dataStore = []
This.top = 0;
This.push = push
This.pop = pop
This.peek = peek
This.length = length;
}

Funktion push(element){
This.dataStore[this.top] = element;
}

Funktion peek(element){
Geben Sie this.dataStore[this.top-1];
zurück }

Funktion pop(){
Geben Sie this.dataStore[--this.top];
zurück }

Funktion clear(){
This.top = 0
}

Funktionslänge(){
Geben Sie this.top
zurück }

Palindrom

Ein Palindrom bezieht sich auf ein Wort, eine Reihe oder eine Phrase, die von vorne bis hinten gleich ist 12321.abcba

Die einfachste Idee eines Palindroms ist, dass, wenn das Element umgekehrt und gleich dem ursprünglichen Element ist, es sich um ein Palindrom handelt

Sie können diese Stack-Klasse verwenden, um hier zu arbeiten

Code kopieren Der Code lautet wie folgt:

Funktion isPalindrome(word) {
var s = new Stack()
for (var i = 0; i < word.length; i ) {
s.push(word[i])
}
var rword = "";
while (s.length() > 0) {
         rword = s.pop();
}
If (word == rword) {
        return true;
} sonst {
         return false;
}
}

isPalindrome("aarra") //false
isPalindrome("aaraa") //true

Sehen Sie sich diese isPalindrome-Funktion an. Sie ruft tatsächlich die Stack-Klasse auf und schiebt dann die an jede zerlegte Einheit übergebenen Wortelemente in den Stapel. Dabei gilt das Prinzip „Last in, first out“. Zerlegen Sie dieses Element mit der Pop-Methode und vergleichen Sie schließlich die Vorher- und Nachher-Assemblierung. Wenn sie gleich sind, handelt es sich um ein Palindrom

Rekursion

Verwenden Sie Rekursion, um einen faktoriellen Algorithmus zu implementieren

5! = 5 * 4 * 3 * 2 * 1 = 120

Rekursion verwenden

Code kopieren Der Code lautet wie folgt:

Funktion Fakultät(n) {
Wenn (n === 0) {
Rückgabe 1;
} sonst {
          return n * Faculty(n - 1);
}
}

Stapeloperationen verwenden

Code kopieren Der Code lautet wie folgt:

Funktion fact(n) {
var s = new Stack()
while (n > 1) {
              //[5,4,3,2]
s.push(n--);
}
var Produkt = 1;
while (s.length() > 0) {
Produkt *= s.pop();
}
Produkt zurückgeben;
}

Fakt(5) //120

Schieben Sie n = 5 dekrementell durch while auf den Stapel und dann durch eine Schleife oder nehmen Sie gemäß dem Last-In-First-Out-Prinzip des Stapels den vordersten heraus und stapeln Sie ihn mit dem Produkt durch die Pop-Methode