Vergleichende Zusammenfassung von zehn nichtlinearen Dimensionsreduktionstechniken beim maschinellen Lernen

Dimensionalitätsreduzierung bedeutet, die Hauptinformationen der Daten so weit wie möglich beizubehalten und gleichzeitig die Anzahl der Features im Datensatz zu reduzieren. Bei Algorithmen zur Dimensionsreduktion handelt es sich um unbeaufsichtigtes Lernen, und der Algorithmus wird anhand unbeschrifteter Daten trainiert.

Obwohl es viele Arten von Dimensionsreduktionsmethoden gibt, können sie alle in zwei Hauptkategorien eingeteilt werden: linear und nichtlinear.

Lineare Methoden projizieren Daten linear von einem hochdimensionalen Raum in einen niedrigdimensionalen Raum (daher der Name lineare Projektion). Beispiele hierfür sind PCA und LDA.

Nichtlineare Methoden sind eine Möglichkeit zur nichtlinearen Dimensionsreduktion und werden häufig verwendet, um die nichtlineare Struktur von Originaldaten zu ermitteln. Methoden zur nichtlinearen Dimensionsreduktion sind besonders wichtig, wenn die Originaldaten nicht einfach linear getrennt werden können. In einigen Fällen wird die nichtlineare Dimensionsreduktion auch als Mannigfaltigkeitslernen bezeichnet. Diese Methode kann hochdimensionale Daten effizienter verarbeiten und dabei helfen, die zugrunde liegende Struktur der Daten aufzudecken. Durch nichtlineare Dimensionsreduktion können wir die Beziehung zwischen Daten besser verstehen, verborgene Muster und Regeln in den Daten entdecken und starke Unterstützung für weitere Datenanalysen und -anwendungen bieten.

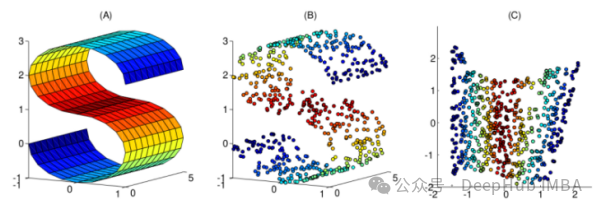
In diesem Artikel wurden 10 häufig verwendete nichtlineare Dimensionsreduktionstechniken zusammengestellt, um Ihnen bei der Auswahl bei Ihrer täglichen Arbeit zu helfen.

1. Kernel-PCA. Möglicherweise kennen Sie die normale PCA, eine lineare Dimensionsreduktionstechnik. Kernel-PCA kann als nichtlineare Version der normalen Hauptkomponentenanalyse betrachtet werden.

Sowohl die Hauptkomponentenanalyse als auch die Kernel-Hauptkomponentenanalyse können zur Dimensionsreduzierung verwendet werden, aber die Kernel-PCA ist effektiver bei der Verarbeitung linear untrennbarer Daten. Der Hauptvorteil von Kernel-PCA besteht darin, nichtlinear trennbare Daten in linear trennbare Daten umzuwandeln und gleichzeitig die Datendimension zu reduzieren. Kernel-PCA kann die nichtlineare Struktur in den Daten durch die Einführung von Kernel-Techniken erfassen und so die Klassifizierungsleistung der Daten verbessern. Daher verfügt die Kernel-PCA über eine stärkere Ausdruckskraft und Generalisierungsfähigkeit beim Umgang mit komplexen Datensätzen.

Wir erstellen zunächst ganz klassische Daten:

import matplotlib.pyplot as plt plt.figure(figsize=[7, 5])  from sklearn.datasets import make_moons X, y = make_moons(n_samples=100, noise=None, random_state=0)  plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='plasma') plt.title('Linearly inseparable data')

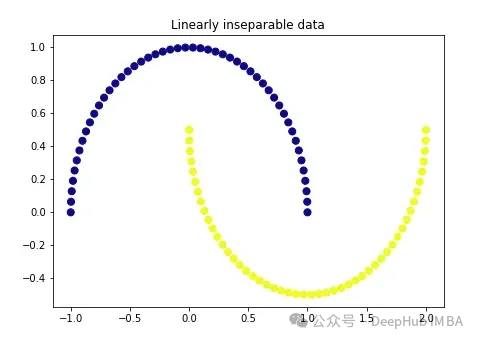Diese beiden Farben repräsentieren zwei linear untrennbare Kategorien. Es ist hier unmöglich, eine gerade Linie zu ziehen, um diese beiden Kategorien zu trennen.

Wir beginnen mit der regulären PCA.

 import numpy as np from sklearn.decomposition import PCA  pca = PCA(n_components=1) X_pca = pca.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_pca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after linear PCA') plt.xlabel('PC1')

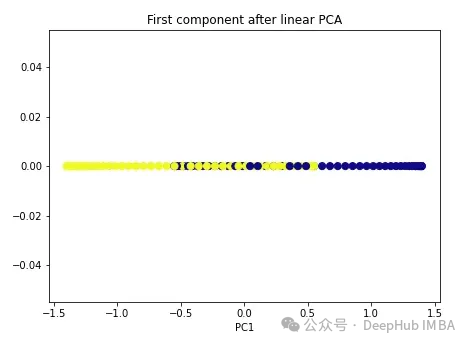Wie Sie sehen können, sind diese beiden Klassen immer noch linear untrennbar. Versuchen wir es nun mit Kernel-PCA.

 import numpy as np from sklearn.decomposition import KernelPCA  kpca = KernelPCA(n_components=1, kernel='rbf', gamma=15) X_kpca = kpca.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_kpca[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.axvline(x=0.0, linestyle='dashed', color='black', linewidth=1.2) plt.title('First component after kernel PCA') plt.xlabel('PC1')

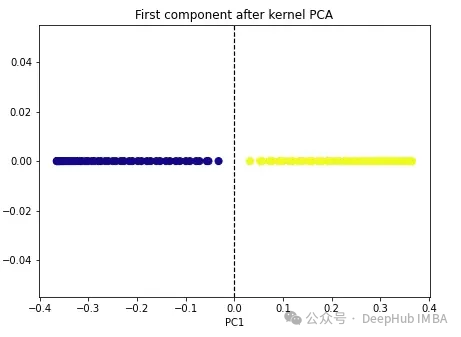Die beiden Klassen werden linear trennbar und der Kernel-PCA-Algorithmus verwendet unterschiedliche Kernel, um Daten von einer Form in eine andere umzuwandeln. Kernel-PCA ist ein zweistufiger Prozess. Zunächst projiziert die Kernelfunktion die Originaldaten vorübergehend in einen hochdimensionalen Raum, in dem die Klassen linear trennbar sind. Der Algorithmus projiziert diese Daten dann zurück auf die niedrigeren Dimensionen, die im Hyperparameter n_components angegeben sind (die Anzahl der Dimensionen, die wir beibehalten möchten).

Es gibt vier Kernel-Optionen in sklearn: linear“, „poly“, „rbf“ und „sigmoid“. Wenn wir den Kernel als „linear“ angeben, wird eine normale PCA durchgeführt. Jeder andere Kernel führt eine nichtlineare PCA durch. Der rbf-Kernel (radiale Basisfunktion) wird am häufigsten verwendet.

2. Multidimensionale Skalierung (MDS)

Multidimensionale Skalierung ist eine weitere nichtlineare Dimensionsreduktionstechnik, die eine Dimensionsreduktion durch Beibehaltung des Abstands zwischen hoch- und niedrigdimensionalen Datenpunkten durchführt. Beispielsweise erscheinen Punkte, die in der ursprünglichen Dimension näher beieinander liegen, auch in der unteren Dimension näher.

Dazu können wir in Scikit-learn die Klasse MDS() verwenden.

 from sklearn.manifold import MDS  mds = MDS(n_components, metric) mds_transformed = mds.fit_transform(X)

metrische Hyperparameter unterscheiden zwei Arten von MDS-Algorithmen: metrische und nichtmetrische. Wenn metric=True, führen Sie metric MDS aus. Andernfalls führen Sie nicht-metrische MDS durch.

Wir wenden zwei Arten von MDS-Algorithmen auf die folgenden nichtlinearen Daten an.

 import numpy as np from sklearn.manifold import MDS  mds = MDS(n_components=1, metric=True) # Metric MDS X_mds = mds.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('Metric MDS') plt.xlabel('Component 1')

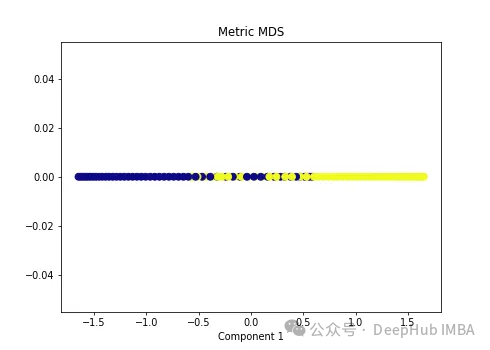
 import numpy as np from sklearn.manifold import MDS  mds = MDS(n_components=1, metric=False) # Non-metric MDS X_mds = mds.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_mds[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('Non-metric MDS') plt.xlabel('Component 1')

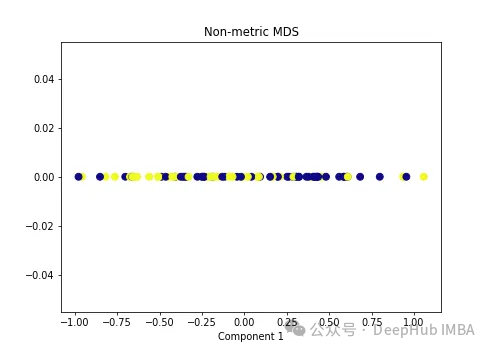
可以看到MDS后都不能使数据线性可分，所以可以说MDS不适合我们这个经典的数据集。

3、Isomap

Isomap(Isometric Mapping)在保持数据点之间的地理距离，即在原始高维空间中的测地线距离或者近似的测地线距离，在低维空间中也被保持。Isomap的基本思想是通过在高维空间中计算数据点之间的测地线距离(通过最短路径算法，比如Dijkstra算法)，然后在低维空间中保持这些距离来进行降维。在这个过程中，Isomap利用了流形假设，即假设高维数据分布在一个低维流形上。因此，Isomap通常在处理非线性数据集时表现良好，尤其是当数据集包含曲线和流形结构时。

 import matplotlib.pyplot as plt plt.figure(figsize=[7, 5])  from sklearn.datasets import make_moons X, y = make_moons(n_samples=100, noise=None, random_state=0)  import numpy as np from sklearn.manifold import Isomap  isomap = Isomap(n_neighbors=5, n_components=1) X_isomap = isomap.fit_transform(X)  plt.figure(figsize=[7, 5]) plt.scatter(X_isomap[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying Isomap') plt.xlabel('Component 1')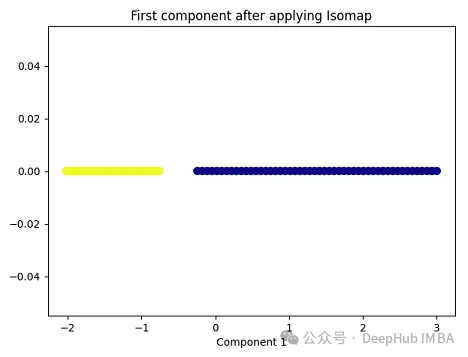

就像核PCA一样，这两个类在应用Isomap后是线性可分的!

4、Locally Linear Embedding(LLE)

与Isomap类似，LLE也是基于流形假设，即假设高维数据分布在一个低维流形上。LLE的主要思想是在局部邻域内保持数据点之间的线性关系，并在低维空间中重构这些关系。

 from sklearn.manifold import LocallyLinearEmbedding lle = LocallyLinearEmbedding(n_neighbors=5,n_components=1) lle_transformed = lle.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(lle_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying LocallyLinearEmbedding') plt.xlabel('Component 1')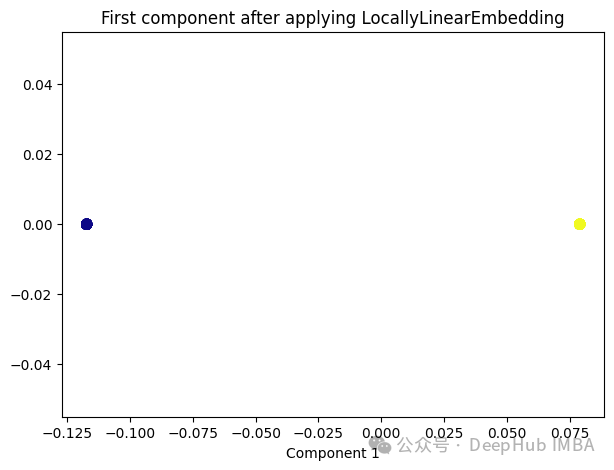

只有2个点，其实并不是这样，我们打印下这个数据

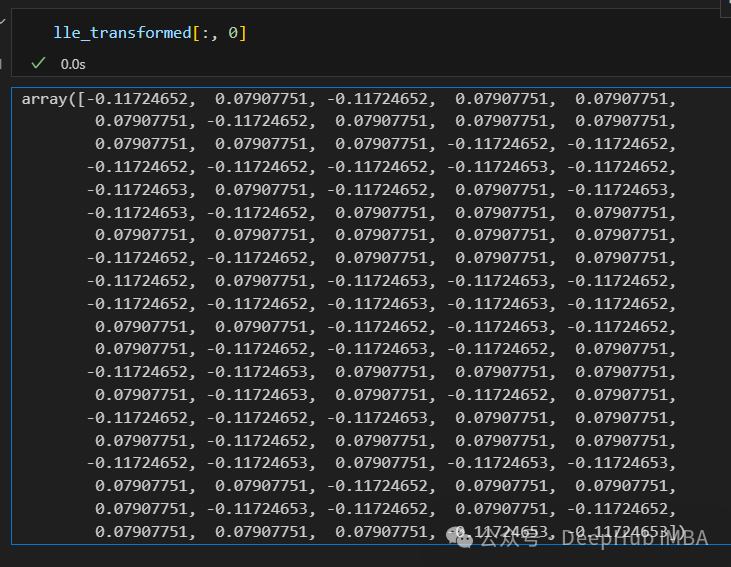
可以看到数据通过降维变成了同一个数字，所以LLE降维后是线性可分的，但是却丢失了数据的信息。

5、Spectral Embedding

Spectral Embedding是一种基于图论和谱理论的降维技术，通常用于将高维数据映射到低维空间。它的核心思想是利用数据的相似性结构，将数据点表示为图的节点，并通过图的谱分解来获取低维表示。

 from sklearn.manifold import SpectralEmbedding sp_emb = SpectralEmbedding(n_components=1, affinity='nearest_neighbors') sp_emb_transformed = sp_emb.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(sp_emb_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying SpectralEmbedding') plt.xlabel('Component 1')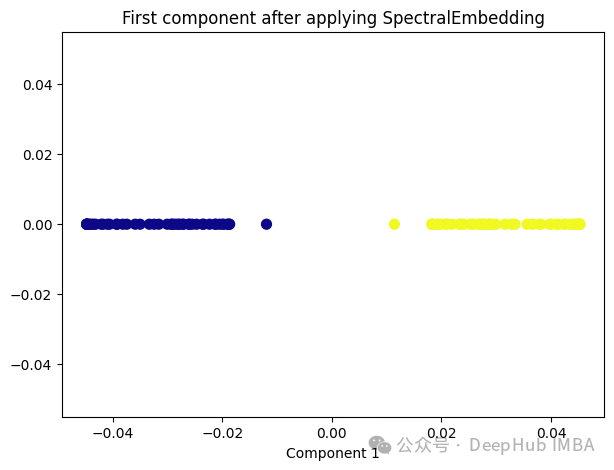

6、t-Distributed Stochastic Neighbor Embedding (t-SNE)

t-SNE的主要目标是保持数据点之间的局部相似性关系，并在低维空间中保持这些关系，同时试图保持全局结构。

from sklearn.manifold import TSNE tsne = TSNE(1, learning_rate='auto', init='pca') tsne_transformed = tsne.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(tsne_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying TSNE') plt.xlabel('Component 1')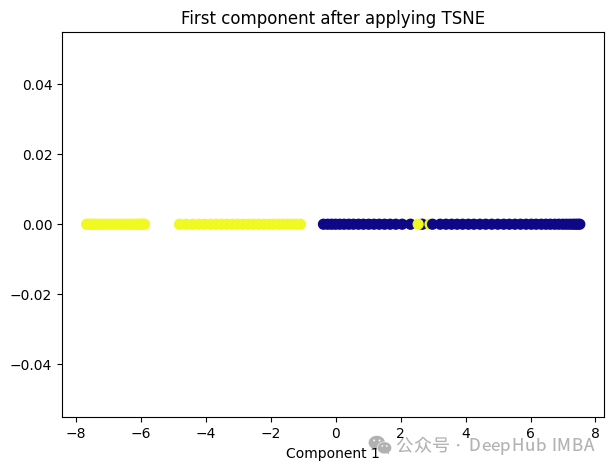

t-SNE好像也不太适合我们的数据。

7、Random Trees Embedding

Random Trees Embedding是一种基于树的降维技术，常用于将高维数据映射到低维空间。它利用了随机森林(Random Forest)的思想，通过构建多棵随机决策树来实现降维。

Random Trees Embedding的基本工作流程：

• 构建随机决策树集合：首先，构建多棵随机决策树。每棵树都是通过从原始数据中随机选择子集进行训练的，这样可以减少过拟合，提高泛化能力。
• 提取特征表示：对于每个数据点，通过将其在每棵树上的叶子节点的索引作为特征，构建一个特征向量。每个叶子节点都代表了数据点在树的某个分支上的位置。
• 降维：通过随机森林中所有树生成的特征向量，将数据点映射到低维空间中。通常使用降维技术，如主成分分析(PCA)或t-SNE等，来实现最终的降维过程。

Random Trees Embedding的优势在于它的计算效率高，特别是对于大规模数据集。由于使用了随机森林的思想，它能够很好地处理高维数据，并且不需要太多的调参过程。

RandomTreesEmbedding使用高维稀疏进行无监督转换，也就是说，我们最终得到的数据并不是一个连续的数值，而是稀疏的表示。所以这里就不进行代码展示了，有兴趣的看看sklearn的sklearn.ensemble.RandomTreesEmbedding

8、Dictionary Learning

Dictionary Learning是一种用于降维和特征提取的技术，它主要用于处理高维数据。它的目标是学习一个字典，该字典由一组原子(或基向量)组成，这些原子是数据的线性组合。通过学习这样的字典，可以将高维数据表示为一个更紧凑的低维空间中的稀疏线性组合。

Dictionary Learning的优点之一是它能够学习出具有可解释性的原子，这些原子可以提供关于数据结构和特征的重要见解。此外，Dictionary Learning还可以产生稀疏表示，从而提供更紧凑的数据表示，有助于降低存储成本和计算复杂度。

 from sklearn.decomposition import DictionaryLearning  dict_lr = DictionaryLearning(n_components=1) dict_lr_transformed = dict_lr.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(dict_lr_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying DictionaryLearning') plt.xlabel('Component 1')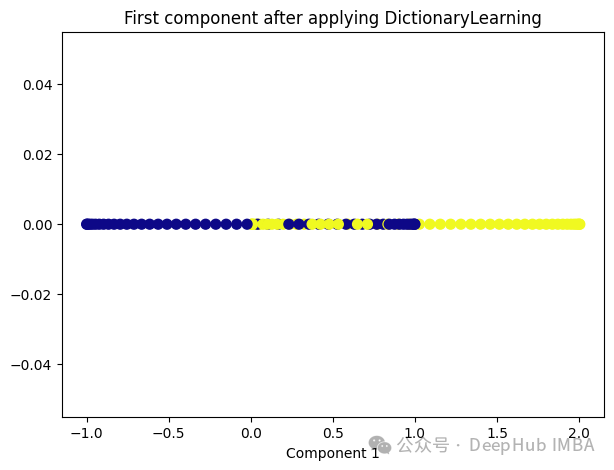

9、Independent Component Analysis (ICA)

Independent Component Analysis (ICA) 是一种用于盲源分离的统计方法，通常用于从混合信号中估计原始信号。在机器学习和信号处理领域，ICA经常用于解决以下问题：

• 盲源分离：给定一组混合信号，其中每个信号是一组原始信号的线性组合，ICA的目标是从混合信号中分离出原始信号，而不需要事先知道混合过程的具体细节。
• 特征提取：ICA可以被用来发现数据中的独立成分，提取数据的潜在结构和特征，通常在降维或预处理过程中使用。

ICA的基本假设是，混合信号中的各个成分是相互独立的，即它们的统计特性是独立的。这与主成分分析(PCA)不同，PCA假设成分之间是正交的，而不是独立的。因此ICA通常比PCA更适用于发现非高斯分布的独立成分。

 from sklearn.decomposition import FastICA  ica = FastICA(n_components=1, whiten='unit-variance') ica_transformed = dict_lr.fit_transform(X) plt.figure(figsize=[7, 5]) plt.scatter(ica_transformed[:, 0], np.zeros((100,1)), c=y, s=50, cmap='plasma') plt.title('First component after applying FastICA') plt.xlabel('Component 1')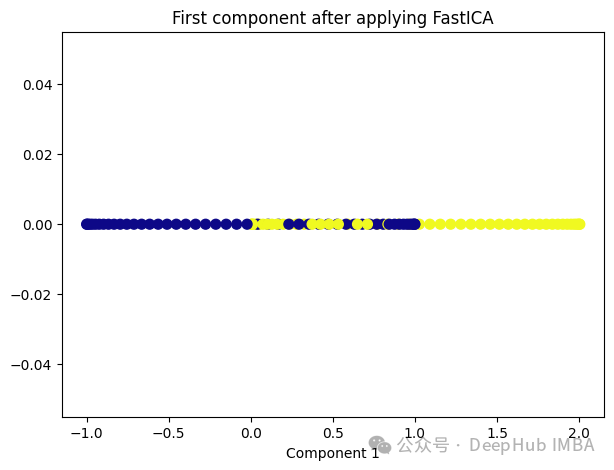

10、Autoencoders (AEs)

到目前为止，我们讨论的NLDR技术属于通用机器学习算法的范畴。而自编码器是一种基于神经网络的NLDR技术，可以很好地处理大型非线性数据。当数据集较小时，自动编码器的效果可能不是很好。

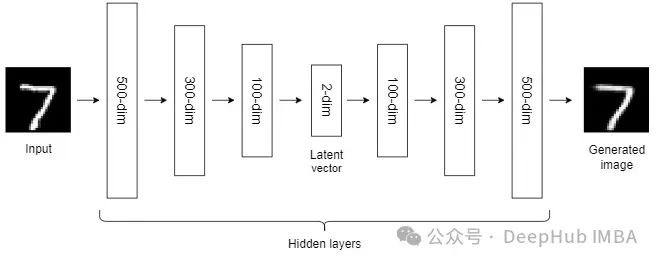
自编码器我们已经介绍过很多次了，所以这里就不详细说明了。

总结

非线性降维技术是一类用于将高维数据映射到低维空间的方法，它们通常适用于数据具有非线性结构的情况。

大多数NLDR方法基于最近邻方法，该方法要求数据中所有特征的尺度相同，所以如果特征的尺度不同，还需要进行缩放。

另外这些非线性降维技术在不同的数据集和任务中可能表现出不同的性能，因此在选择合适的方法时需要考虑数据的特征、降维的目标以及计算资源等因素。

Das obige ist der detaillierte Inhalt vonVergleichende Zusammenfassung von zehn nichtlinearen Dimensionsreduktionstechniken beim maschinellen Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!