[Bearbeiten] Die charakteristische Funktion kann durch Fourier-Transformation der Wahrscheinlichkeitsdichtefunktion erhalten werden. Es besteht eine Eins-zu-Eins-Beziehung zwischen der charakteristischen Funktion und der Wahrscheinlichkeitsdichtefunktion. Daher ist die Kenntnis der charakteristischen Funktion einer Verteilung gleichbedeutend mit der Kenntnis der Wahrscheinlichkeitsdichtefunktion einer Verteilung. da:Sandsynlighedstæthedsfunktion en:Probability Density Function it:Funzione di densità di probabilità nl:Kansdichtheid sv:TäthetsfunktionEin Partikelstrahl wird durch ein Hindernis (befindet sich bei x = 0) zerstreut. Seine Wellenfunktion ist wie folgt: Ψ(x, t) = Ae-iEt/h[wenn x
Ψ(x, t) = e-iEt/h( Beikx+ Ce-ikx) [wenn x> 0 ]
Wobei E = h2k2/( 2m ) und k > 0, sind A, B und C komplexe Koeffizienten.
﹝Das „h“ ist „h-bar“, also die horizontale Linie über h﹞
(a) Berechnen Sie die Wahrscheinlichkeitsdichte p(x, t), wenn x
(b) Berechnen Sie die Wahrscheinlichkeit der Flussdichte j(x, t), wenn x
(c) Berechnen Sie die Wahrscheinlichkeitsdichte p(x, t), wenn x > 0.
(d) Berechnen Sie die Wahrscheinlichkeit der Flussdichte j(x, t), wenn x > 0.
(e) Die obige Wellenfunktion enthält drei verschiedene Teile, drei Koeffizienten A, B und C. Sagen Sie, ob sich jeder nach rechts oder links bewegt. Die drei stehen für Einfall, Reflexion und Emission. Welches ist das?
Hinweis: Die Antworten auf p(x, t) und j(x, t) müssen reelle Zahlen sein.
Wie man zwischen Wahrscheinlichkeitsfunktion und Wahrscheinlichkeitsdichte unterscheidet
Mathematische Definition der Wahrscheinlichkeitsdichte
Wenn es für die Zufallsvariable
Kontinuierliche Zufallsvariablen werden oft intuitiv durch ihre Wahrscheinlichkeitsdichtefunktionen beschrieben. Die Wahrscheinlichkeitsdichtefunktion f(x) kontinuierlicher Zufallsvariablen hat die folgenden Eigenschaften:
Dies bezieht sich auf eindimensionale kontinuierliche Zufallsvariablen, und mehrdimensionale kontinuierliche Variablen sind ähnlich.
Wahrscheinlichkeitsdichtefunktion von Zufallsdaten: Stellt die Wahrscheinlichkeit dar, dass die momentane Amplitude in einen bestimmten Bereich fällt, und ist daher eine Funktion der Amplitude. Sie variiert mit der Größe des eingenommenen Bereichs.
Die Dichtefunktion f(x) hat die folgenden Eigenschaften:
(1)f(x)≧0;
(2) ∫f(x)d(x)=1;
(3) P(a
Angenommen, die Wahrscheinlichkeitsdichtefunktion der Zufallsvariablen X N0 1 Y |x|
Der Problemlösungsprozess ist wie folgt: 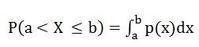
Erweiterte Informationen
Wahrscheinlichkeitsdichtemethode: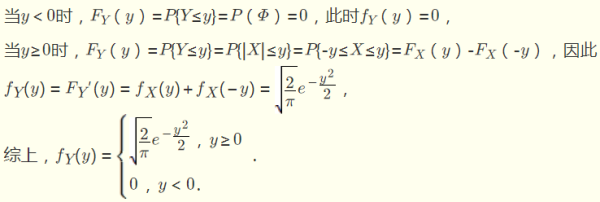
Angenommen, die Zufallsvariable Unter diesen ist α=min(g(-∞), g(∞)), β=max(g(-∞), g(∞)), h(y) die Umkehrfunktion von g(x).
Einfach über die Wahrscheinlichkeitsdichte zu sprechen, hat keine praktische Bedeutung. Sie muss ein bestimmtes begrenztes Intervall als Prämisse haben. Die Wahrscheinlichkeitsdichte kann als Ordinate und das Intervall als Abszisse betrachtet werden. Das Integral der Wahrscheinlichkeitsdichte über das Intervall ist die Fläche, und diese Fläche ist die Wahrscheinlichkeit, dass ein Ereignis in diesem Intervall auftritt . Daher ist es sinnlos, die Wahrscheinlichkeitsdichte eines Punktes allein zu analysieren. Er muss ein Intervall als Referenz und Vergleich haben.
Wahrscheinlichkeit bezieht sich auf die Wahrscheinlichkeit, dass ein Ereignis zufällig auftritt. Bei einer gleichmäßigen Verteilungsfunktion ist die Wahrscheinlichkeitsdichte gleich der Wahrscheinlichkeit eines Intervalls (dem Wertebereich des Ereignisses) geteilt durch die Länge des Intervalls. negativ und kann sehr groß oder sehr klein sein.
Wählen Sie zufällig ein Produkt aus einer Charge echter und fehlerhafter Produkte aus, und „das, das Sie ziehen, ist echt“ ist ein Zufallsereignis. Angenommen, ein Zufallsphänomen wird n-mal getestet und beobachtet, und Ereignis A tritt m-mal auf, d. h. seine Auftrittshäufigkeit beträgt m/n. Nach vielen wiederholten Experimenten nähert sich m/n oft immer mehr einer bestimmten Konstante (siehe Bernoullis Gesetz der großen Zahlen zum Beweis dieser Schlussfolgerung).

