 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte KI
KI TimePillars: Wo kann die reine LiDAR-3D-Erkennungsroute erweitert werden? Direkte Abdeckung von 200m!
TimePillars: Wo kann die reine LiDAR-3D-Erkennungsroute erweitert werden? Direkte Abdeckung von 200m!TimePillars: Wo kann die reine LiDAR-3D-Erkennungsroute erweitert werden? Direkte Abdeckung von 200m!
Die 3D-Objekterkennung auf Basis der LiDAR-Punktwolke ist ein sehr klassisches Problem. Sowohl die Wissenschaft als auch die Industrie haben verschiedene Modelle vorgeschlagen, um Genauigkeit, Geschwindigkeit und Robustheit zu verbessern. Aufgrund der komplexen Außenumgebung ist die Leistung der Objekterkennung für Punktwolken im Freien jedoch nicht sehr gut. Lidar-Punktwolken sind von Natur aus spärlich. Wie kann dieses Problem gezielt gelöst werden? Das Papier gibt seine eigene Antwort: Extrahieren Sie Informationen basierend auf der Aggregation von Zeitreiheninformationen.
Vorher geschrieben

In diesem Artikel geht es hauptsächlich um eine wichtige Herausforderung beim autonomen Fahren: wie man eine genaue dreidimensionale Darstellung der Umgebung erstellt. Dies ist entscheidend für die Gewährleistung der Zuverlässigkeit und Sicherheit autonomer Fahrzeuge. Insbesondere müssen autonome Fahrzeuge in der Lage sein, umliegende Objekte wie Fahrzeuge und Fußgänger zu erkennen und deren Position, Größe und Ausrichtung genau zu bestimmen. Typischerweise verwenden Menschen tiefe neuronale Netze, um LiDAR-Daten zu verarbeiten und diese Aufgabe zu erfüllen.
Aktuelle Forschung konzentriert sich hauptsächlich auf Single-Frame-Methoden, also die Verwendung von Daten aus jeweils einem Sensorscan. Diese Methode schneidet bei klassischen Benchmarks gut ab und erkennt Objekte in Entfernungen von bis zu 75 Metern. Allerdings ist die Spärlichkeit von Lidar-Punktwolken besonders auf große Entfernungen deutlich zu erkennen. Daher sind die Forscher der Ansicht, dass es nicht ausreicht, sich allein auf einen einzigen Scan zur Erkennung über große Entfernungen zu verlassen, beispielsweise bis zu einer Entfernung von 200 Metern. Daher muss sich die zukünftige Forschung auf die Bewältigung dieser Herausforderung konzentrieren.
Um dieses Problem zu lösen, besteht eine Möglichkeit darin, die Punktwolkenaggregation zu verwenden, bei der eine Reihe von LIDAR-Scandaten verkettet werden, um eine dichtere Eingabe zu erhalten. Dieser Ansatz ist jedoch rechenintensiv und nutzt die Aggregation innerhalb des Netzwerks nicht vollständig aus. Um die Rechenkosten zu senken und Informationen besser zu nutzen, sollten Sie die Verwendung rekursiver Methoden in Betracht ziehen. Rekursive Methoden sammeln Informationen im Laufe der Zeit und erzeugen genauere Ausgaben, indem sie die aktuelle Eingabe iterativ mit früheren aggregierten Ergebnissen fusionieren. Diese Methode kann nicht nur die Berechnungseffizienz verbessern, sondern auch historische Informationen effektiv nutzen, um die Vorhersagegenauigkeit zu verbessern. Rekursive Methoden finden breite Anwendung bei Punktwolkenaggregationsproblemen und haben zufriedenstellende Ergebnisse erzielt.
In dem Artikel wurde auch erwähnt, dass zur Vergrößerung des Erkennungsbereichs einige erweiterte Operationen verwendet werden können, z. B. spärliche Faltung, Aufmerksamkeitsmodul und 3D-Faltung. Allerdings ignorieren diese Vorgänge normalerweise die Kompatibilitätsprobleme der Zielhardware. Beim Einsatz und Training neuronaler Netze unterscheidet sich die verwendete Hardware häufig erheblich in Bezug auf unterstützte Vorgänge und Latenz. Beispielsweise unterstützt Zielhardware wie Nvidia Orin DLA häufig keine Vorgänge wie Sparse Convolution oder Attention. Darüber hinaus ist die Verwendung von Ebenen wie 3D-Faltungen aufgrund der Anforderungen an die Echtzeitlatenz häufig nicht möglich. Dies unterstreicht die Notwendigkeit, einfache Operationen wie die 2D-Faltung zu verwenden.
Das Papier schlägt ein neues zeitlich rekursives Modell vor, TimePillars, das den Satz von Operationen berücksichtigt, die auf gemeinsamer Zielhardware unterstützt werden, auf 2D-Faltung basiert, auf der Eingabedarstellung einer Punktsäule (Pillar) und einer Faltungsrekursiveinheit basiert. Mithilfe einer einzelnen Faltung und Hilfslernen wird die Eigenbewegungskompensation auf den verborgenen Zustand der wiederkehrenden Einheit angewendet. Der Einsatz von Hilfsaufgaben zur Sicherstellung der Korrektheit dieser Manipulation hat sich in Ablationsstudien als angemessen erwiesen. Das Papier untersucht auch die optimale Platzierung des rekursiven Moduls in der Pipeline und zeigt deutlich, dass die beste Leistung erzielt wird, wenn es zwischen dem Backbone des Netzwerks und dem Erkennungskopf platziert wird. Am neu veröffentlichten Zenseact Open Dataset (ZOD) demonstriert das Papier die Wirksamkeit der TimePillars-Methode. Im Vergleich zu Single-Frame- und Multi-Frame-Point-and-Pillar-Basislinien erzielt TimePillars erhebliche Verbesserungen der Auswertungsleistung, insbesondere bei der Erkennung über große Entfernungen (bis zu 200 Meter) in den wichtigen Kategorien Radfahrer und Fußgänger. Schließlich haben TimePillars eine deutlich geringere Latenz als Multi-Frame-Punktsäulen, wodurch sie für Echtzeitsysteme geeignet sind.
Dieses Papier schlägt ein neues zeitlich rekursives Modell namens TimePillars vor, um die Aufgabe der 3D-Lidar-Objekterkennung zu lösen, und berücksichtigt die Reihe von Operationen, die von gängiger Zielhardware unterstützt werden. Experimente haben gezeigt, dass TimePillars bei der Fernerkennung eine deutlich bessere Leistung als Single-Frame- und Multi-Frame-Point-Pillar-Basislinien erzielt. Darüber hinaus bewertet das Papier erstmals ein 3D-Lidar-Objekterkennungsmodell anhand des offenen Datensatzes von Zenseact. Die Einschränkungen des Papiers bestehen jedoch darin, dass es sich nur auf LiDAR-Daten konzentriert, andere Sensoreingaben nicht berücksichtigt und seinen Ansatz auf einer einzigen Basislinie auf dem neuesten Stand der Technik basiert. Nichtsdestotrotz sind die Autoren davon überzeugt, dass ihr Rahmenwerk allgemeingültig ist, d. h. zukünftige Verbesserungen der Basislinie werden sich in Gesamtleistungsverbesserungen niederschlagen.
Detaillierte Erklärung von TimePillars

Eingabevorverarbeitung
Im Abschnitt „Eingabevorverarbeitung“ dieses Dokuments verwendet der Autor eine Technik namens „Pillarisierung“, um die Eingabepunktwolkendaten zu verarbeiten. Im Gegensatz zur herkömmlichen Voxelisierung segmentiert diese Methode die Punktwolke in vertikale Säulenstrukturen, wobei die Segmentierung nur in horizontaler Richtung (x- und y-Achse) erfolgt, während in vertikaler Richtung (z-Achse) eine feste Höhe beibehalten wird. Der Vorteil dieser Verarbeitungsmethode besteht darin, dass sie die Konsistenz der Netzwerkeingabegröße aufrechterhalten und die 2D-Faltung für eine effiziente Verarbeitung nutzen kann. Auf diese Weise können Punktwolkendaten effizient verarbeitet werden und liefern genauere und zuverlässigere Eingaben für nachfolgende Aufgaben.
Ein Problem bei der Pillarisierung besteht jedoch darin, dass sie viele leere Spalten erzeugt, was zu sehr spärlichen Daten führt. Um dieses Problem zu lösen, schlägt das Papier den Einsatz der dynamischen Voxelisierungstechnologie vor. Diese Technik vermeidet die Notwendigkeit, für jede Spalte eine vordefinierte Anzahl von Punkten zu haben, wodurch Kürzungs- oder Fülloperationen für jede Spalte entfallen. Stattdessen werden die gesamten Punktwolkendaten als Ganzes verarbeitet, um der erforderlichen Gesamtpunktzahl zu entsprechen, die hier auf 200.000 Punkte festgelegt ist. Der Vorteil dieser Vorverarbeitungsmethode besteht darin, dass sie den Informationsverlust minimiert und die generierte Datendarstellung stabiler und konsistenter macht.
Modellarchitektur
Dann stellt der Autor für die Modellarchitektur detailliert eine neuronale Netzwerkarchitektur vor, die aus einem Pillar-Feature-Encoder (Pillar Feature Encoder), einem 2D-Convolutional Neural Network (CNN)-Backbone und einem Erkennungskopf besteht.
- Pillar Feature Encoder: Dieser Teil ordnet den vorverarbeiteten Eingabetensor einem BEV-Pseudobild (Bird's Eye View) zu. Nach Verwendung der dynamischen Voxelisierung wird das vereinfachte PointNet entsprechend angepasst. Die Eingabe wird durch 1D-Faltung, Batch-Normalisierung und ReLU-Aktivierungsfunktion verarbeitet, was zu einem Tensor mit der Form führt, wobei die Anzahl der Kanäle darstellt. Vor der letzten Scatter-Max-Schicht wird Max-Pooling auf die Kanäle angewendet, wodurch ein latenter Formraum entsteht . Da der anfängliche Tensor als codiert ist, was nach der vorherigen Ebene zu wird, wird die Max-Pooling-Operation entfernt.
- Backbone: Verwendung der im ursprünglichen Säulenpapier vorgeschlagenen 2D-CNN-Backbone-Architektur aufgrund ihrer überlegenen Tiefeneffizienz. Der latente Raum wird mithilfe von drei Downsampling-Blöcken (Conv2D-BN-ReLU) reduziert und mithilfe von drei Upsampling-Blöcken und transponierter Faltung mit einer Ausgabeform von wiederhergestellt.
- Speichereinheit: Modellieren Sie den Speicher des Systems als wiederkehrendes neuronales Netzwerk (RNN), insbesondere unter Verwendung von Faltungs-GRU (convGRU), der Faltungsversion von Gated Recurrent Unit. Der Vorteil der Faltungs-GRU besteht darin, dass sie das Problem des verschwindenden Gradienten vermeidet und die Effizienz verbessert, während die räumlichen Dateneigenschaften erhalten bleiben. Im Vergleich zu anderen Optionen wie LSTM verfügt GRU aufgrund der geringeren Anzahl von Gattern über weniger trainierbare Parameter und kann als Speicherregulierungstechnik betrachtet werden (die die Komplexität der verborgenen Zustände verringert). Durch die Zusammenführung von Vorgängen ähnlicher Art wird die Anzahl der erforderlichen Faltungsschichten reduziert, wodurch die Einheit effizienter wird.
- Erkennungskopf: Eine einfache Modifikation des SSD (Single Shot MultiBox Detector). Das Kernkonzept von SSD bleibt erhalten, d. h. ein einzelner Durchgang ohne Regionsvorschlag, die Verwendung von Ankerboxen wird jedoch eliminiert. Die direkte Ausgabe von Vorhersagen für jede Zelle im Raster vermeidet zwar die Fähigkeit zur Erkennung mehrerer Zellenobjekte, vermeidet jedoch mühsame und oft ungenaue Anpassungen der Ankerbox-Parameter und vereinfacht den Inferenzprozess. Die lineare Ebene verarbeitet die jeweiligen Ausgaben der Klassifizierung und Lokalisierungsregression (Position, Größe und Winkel). Nur die Größe verwendet eine Aktivierungsfunktion (ReLU), um die Annahme negativer Werte zu verhindern. Darüber hinaus vermeidet dieser Artikel im Gegensatz zur einschlägigen Literatur das Problem der direkten Winkelregression, indem er die Sinus- und Cosinuskomponenten der Fahrtrichtung des Fahrzeugs unabhängig vorhersagt und daraus Winkel extrahiert.
Feature Ego-Motion Compensation
In diesem Teil des Artikels diskutiert der Autor, wie die von der Faltungs-GRU ausgegebenen verborgenen Zustandsmerkmale verarbeitet werden, die durch das Koordinatensystem des vorherigen Frames dargestellt werden. Bei direkter Speicherung und Verwendung zur Berechnung der nächsten Vorhersage kommt es aufgrund der Eigenbewegung zu einer räumlichen Nichtübereinstimmung.
Für die Konvertierung können verschiedene Techniken angewendet werden. Im Idealfall würden die korrigierten Daten in das Netzwerk eingespeist und nicht innerhalb des Netzwerks transformiert. Dies ist jedoch nicht die in der Arbeit vorgeschlagene Methode, da sie das Zurücksetzen der verborgenen Zustände bei jedem Schritt im Inferenzprozess, die Transformation der vorherigen Punktwolken und deren Verbreitung im gesamten Netzwerk erfordert. Dies ist nicht nur ineffizient, es macht auch den Zweck der Verwendung von RNNs zunichte. Daher muss in einem Schleifenkontext die Kompensation auf Feature-Ebene erfolgen. Dies macht die hypothetische Lösung effizienter, macht das Problem aber auch komplexer. Herkömmliche Interpolationsmethoden können verwendet werden, um Merkmale in transformierten Koordinatensystemen zu erhalten.
Im Gegensatz dazu schlägt das Papier, inspiriert von der Arbeit von Chen et al., vor, Faltungsoperationen und Hilfsaufgaben zur Durchführung von Transformationen zu verwenden. Unter Berücksichtigung der begrenzten Details der oben genannten Arbeit schlägt das Papier eine maßgeschneiderte Lösung für dieses Problem vor.
Der in der Arbeit verfolgte Ansatz besteht darin, das Netzwerk über eine zusätzliche Faltungsschicht mit den Informationen zu versorgen, die zur Durchführung der Merkmalstransformation erforderlich sind. Zuerst wird die relative Transformationsmatrix zwischen zwei aufeinanderfolgenden Frames berechnet, d. h. die Operationen, die für eine erfolgreiche Transformation von Merkmalen erforderlich sind. Extrahieren Sie dann die 2D-Informationen (Rotations- und Translationsteil) daraus:
Diese Vereinfachung vermeidet die Hauptmatrixkonstanten und funktioniert im 2D-Bereich (Pseudobild), wodurch 16 Werte auf 6 reduziert werden. Anschließend wird die Matrix abgeflacht und erweitert, um sie an die Form der zu kompensierenden verborgenen Merkmale anzupassen. Die erste Dimension stellt die Anzahl der Frames dar, die konvertiert werden müssen. Diese Darstellung eignet sich für die Verkettung jeder potenziellen Säule in der Kanaldimension des verborgenen Features.
Abschließend werden die verborgenen Zustandsmerkmale in eine 2D-Faltungsschicht eingespeist, die an den Transformationsprozess angepasst ist. Ein wichtiger Aspekt ist, dass die Durchführung einer Faltung nicht garantiert, dass die Transformation stattfindet. Durch die Kanalverkettung erhält das Netzwerk lediglich zusätzliche Informationen darüber, wie die Transformation durchgeführt werden könnte. In diesem Fall bietet sich der Einsatz von assistiertem Lernen an. Während des Trainings wird parallel zum Hauptziel (Objekterkennung) ein zusätzliches Lernziel (Koordinatentransformation) hinzugefügt. Es wird eine Hilfsaufgabe entworfen, deren Zweck darin besteht, das Netzwerk unter Aufsicht durch den Transformationsprozess zu führen, um die Korrektheit der Kompensation sicherzustellen. Die Hilfsaufgabe ist auf den Trainingsprozess beschränkt. Sobald das Netzwerk lernt, Features korrekt zu transformieren, verliert es seine Anwendbarkeit. Daher wird diese Aufgabe bei der Inferenz nicht berücksichtigt. Im nächsten Abschnitt werden weitere Experimente durchgeführt, um die Auswirkungen zu vergleichen.
Experimente

Experimentelle Ergebnisse zeigen, dass das TimePillars-Modell bei der Verarbeitung des ZOD-Frame-Datensatzes (Zenseact Open Dataset) eine gute Leistung erbringt, insbesondere bei der Verarbeitung von Entfernungen bis zu 120 Metern. Diese Ergebnisse verdeutlichen die Leistungsunterschiede von TimePillars bei verschiedenen Bewegungstransformationsmethoden und vergleichen sie mit anderen Methoden.
Nach dem Vergleich des Basismodells PointPillars und des Multi-Frame (MF) PointPillars ist ersichtlich, dass TimePillars bei mehreren wichtigen Leistungsindikatoren erhebliche Verbesserungen erzielt hat. Insbesondere beim NuScenes Detection Score (NDS) weist TimePillars eine höhere Gesamtpunktzahl auf, was seine Vorteile bei der Erkennungsleistung und Positionierungsgenauigkeit widerspiegelt. Darüber hinaus erzielte TimePillars auch niedrigere Werte beim durchschnittlichen Konvertierungsfehler (mATE), dem durchschnittlichen Skalenfehler (mASE) und dem durchschnittlichen Orientierungsfehler (mAOE), was darauf hinweist, dass es präziser in der Positionierungsgenauigkeit und Orientierungsschätzung ist. Besonders hervorzuheben ist, dass die unterschiedlichen Implementierungen von TimePillars im Hinblick auf die Bewegungskonvertierung einen erheblichen Einfluss auf die Leistung haben. Bei Verwendung der faltungsbasierten Bewegungstransformation (Conv-basiert) schneidet TimePillars besonders gut bei NDS, mATE, mASE und mAOE ab und beweist die Wirksamkeit dieser Methode bei der Bewegungskompensation und der Verbesserung der Erkennungsgenauigkeit. Im Gegensatz dazu übertrifft TimePillars mit der Interpolationsmethode ebenfalls das Basismodell, ist jedoch in einigen Indikatoren der Faltungsmethode unterlegen. Die Ergebnisse der durchschnittlichen Präzision (mAP) zeigen, dass TimePillars bei der Erkennung von Fahrzeugen, Radfahrern und Fußgängerkategorien gut abschneidet, insbesondere bei anspruchsvolleren Kategorien wie Radfahrern und Fußgängern ist die Leistungsverbesserung deutlicher. Aus Sicht der Verarbeitungsfrequenz (f (Hz)) sind TimePillars zwar nicht so schnell wie Single-Frame-PointPillars, aber schneller als Multi-Frame-PointPillars und behalten gleichzeitig eine hohe Erkennungsleistung bei. Dies zeigt, dass TimePillars eine effektive Fernerkennung und Bewegungskompensation durchführen und gleichzeitig die Echtzeitverarbeitung aufrechterhalten kann. Mit anderen Worten: Das TimePillars-Modell weist erhebliche Vorteile bei der Fernerkennung, Bewegungskompensation und Verarbeitungsgeschwindigkeit auf, insbesondere bei der Verarbeitung von Multiframe-Daten und der Verwendung einer faltungsbasierten Bewegungskonvertierungstechnologie. Diese Ergebnisse verdeutlichen das Anwendungspotenzial von TimePillars im Bereich der 3D-Lidar-Objekterkennung für autonome Fahrzeuge.

Die oben genannten experimentellen Ergebnisse zeigen, dass das TimePillars-Modell bei der Objekterkennung in verschiedenen Entfernungsbereichen eine hervorragende Leistung erbringt, insbesondere im Vergleich zum Benchmark-Modell PointPillars. Diese Ergebnisse sind in drei Haupterkennungsbereiche unterteilt: 0 bis 50 Meter, 50 bis 100 Meter und über 100 Meter.
Zuallererst sind der NuScenes Detection Score (NDS) und die Average Precision (mAP) die Gesamtleistungsindikatoren. TimePillars übertrifft PointPillars in beiden Metriken und weist insgesamt höhere Erkennungsfähigkeiten und Positionierungsgenauigkeit auf. Konkret liegt der NDS von TimePillars bei 0,723, was viel höher ist als der von PointPillars mit 0,657. In Bezug auf den mAP übertrifft TimePillars mit 0,570 auch deutlich den Wert von 0,475.

Im Leistungsvergleich innerhalb verschiedener Distanzbereiche zeigt sich, dass TimePillars in jedem Bereich besser abschneidet. Für die Fahrzeugkategorie beträgt die Erkennungsgenauigkeit von TimePillars in den Bereichen 0 bis 50 Meter, 50 bis 100 Meter und über 100 Meter 0,884, 0,776 bzw. 0,591, was allesamt höher ist als die Leistung von PointPillars im gleichen Bereich. Dies zeigt, dass TimePillars eine höhere Genauigkeit bei der Fahrzeugerkennung aufweist, sowohl im Nah- als auch im Fernbereich. TimePillars zeigte auch eine bessere Erkennungsleistung beim Umgang mit gefährdeten Fahrzeugen (wie Motorrädern, Rollstühlen, Elektrorollern usw.). Insbesondere im Bereich von mehr als 100 Metern beträgt die Erkennungsgenauigkeit von TimePillars 0,178, während PointPillars nur 0,036 beträgt, was erhebliche Vorteile bei der Erkennung über große Entfernungen zeigt. Bei der Fußgängererkennung zeigte TimePillars ebenfalls eine bessere Leistung, insbesondere im Bereich von 50 bis 100 Metern, mit einer Erkennungsgenauigkeit von 0,350, während PointPillars nur 0,211 betrug. Selbst auf größere Entfernungen (über 100 Meter) erreicht TimePillars noch eine gewisse Erkennungsgenauigkeit (Genauigkeit von 0,032), während PointPillars in dieser Entfernung keine Leistung erbringt.
Diese experimentellen Ergebnisse unterstreichen die überlegene Leistung von TimePillars bei der Bewältigung von Objekterkennungsaufgaben in verschiedenen Entfernungsbereichen. Ob im Nahbereich oder im anspruchsvolleren Fernbereich, TimePillars liefern genauere und zuverlässigere Erkennungsergebnisse, die für die Sicherheit und Effizienz autonomer Fahrzeuge von entscheidender Bedeutung sind.
Diskussion

Der Hauptvorteil des TimePillars-Modells ist zunächst seine Wirksamkeit bei der Objekterkennung über große Entfernungen. Durch den Einsatz dynamischer Voxelisierung und Faltungs-GRU-Strukturen ist das Modell besser in der Lage, spärliche LIDAR-Daten zu verarbeiten, insbesondere bei der Objekterkennung über große Entfernungen. Dies ist entscheidend für den sicheren Betrieb autonomer Fahrzeuge in komplexen und sich verändernden Straßenumgebungen. Darüber hinaus zeigt das Modell auch eine gute Leistung hinsichtlich der Verarbeitungsgeschwindigkeit, was für Echtzeitanwendungen unerlässlich ist. Andererseits verwendet TimePillars eine faltungsbasierte Methode zur Bewegungskompensation, was eine wesentliche Verbesserung gegenüber herkömmlichen Methoden darstellt. Dieser Ansatz stellt die Korrektheit der Transformation durch Hilfsaufgaben während des Trainings sicher und verbessert so die Genauigkeit des Modells beim Umgang mit bewegten Objekten.
Allerdings weist die Forschung dieser Arbeit auch einige Einschränkungen auf. Erstens schneidet TimePillars zwar gut bei der Erkennung entfernter Objekte ab, diese Leistungssteigerung kann jedoch zu Lasten einer gewissen Verarbeitungsgeschwindigkeit gehen. Die Geschwindigkeit des Modells ist zwar immer noch für Echtzeitanwendungen geeignet, im Vergleich zu Single-Frame-Methoden ist sie jedoch immer noch geringer. Darüber hinaus konzentriert sich das Papier hauptsächlich auf LiDAR-Daten und berücksichtigt keine anderen Sensoreingaben wie Kameras oder Radare, was die Anwendung des Modells in komplexeren Multisensorumgebungen einschränken könnte.
Das heißt, TimePillars hat erhebliche Vorteile bei der 3D-Lidar-Objekterkennung für autonome Fahrzeuge gezeigt, insbesondere bei der Fernerkennung und Bewegungskompensation. Trotz des leichten Kompromisses bei der Verarbeitungsgeschwindigkeit und Einschränkungen bei der Verarbeitung von Multisensordaten stellt TimePillars immer noch einen wichtigen Fortschritt auf diesem Gebiet dar.
Fazit
Diese Arbeit zeigt, dass die Berücksichtigung vergangener Sensordaten der bloßen Nutzung aktueller Informationen überlegen ist. Der Zugriff auf frühere Fahrumgebungsinformationen kann die spärliche Beschaffenheit von LIDAR-Punktwolken bewältigen und zu genaueren Vorhersagen führen. Wir zeigen, dass rekurrente Netzwerke als Mittel geeignet sind, Letzteres zu erreichen. Die Bereitstellung von Systemspeicher führt zu einer robusteren Lösung im Vergleich zu Punktwolken-Aggregationsmethoden, die durch umfangreiche Verarbeitung dichtere Datendarstellungen erstellen. Die von uns vorgeschlagene Methode TimePillars implementiert eine Möglichkeit zur Lösung des rekursiven Problems. Indem wir einfach drei zusätzliche Faltungsschichten zum Inferenzprozess hinzufügen, zeigen wir, dass grundlegende Netzwerkbausteine ausreichen, um signifikante Ergebnisse zu erzielen und sicherzustellen, dass bestehende Effizienz- und Hardware-Integrationsspezifikationen erfüllt werden. Nach unserem besten Wissen liefert diese Arbeit die ersten Benchmark-Ergebnisse für die 3D-Objekterkennungsaufgabe auf dem neu eingeführten offenen Zenseact-Datensatz. Wir hoffen, dass unsere Arbeit in Zukunft zu sichereren und nachhaltigeren Straßen beitragen kann.
Das obige ist der detaillierte Inhalt vonTimePillars: Wo kann die reine LiDAR-3D-Erkennungsroute erweitert werden? Direkte Abdeckung von 200m!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Die verborgenen Gefahren des internen Einsatzes der KI: Governance -Lücken und katastrophale RisikenApr 28, 2025 am 11:12 AM
Die verborgenen Gefahren des internen Einsatzes der KI: Governance -Lücken und katastrophale RisikenApr 28, 2025 am 11:12 AMLaut einem neuen Bericht der Apollo Research stellt die nicht kontrollierte interne Bereitstellung fortschrittlicher KI -Systeme erhebliche Risiken dar. Dieser mangelnde Aufsicht, der bei großen KI -Unternehmen weit verbreitet ist
 Bauen des AI PolygraphenApr 28, 2025 am 11:11 AM
Bauen des AI PolygraphenApr 28, 2025 am 11:11 AMTraditionelle Lügendetektoren sind veraltet. Wenn man sich auf den vom Armband verbundenen Zeiger stützt, ist ein Lügendetektor, der die lebenswichtigen Anzeichen und physikalischen Reaktionen des Probanden ausdruckt, bei der Identifizierung von Lügen nicht genau. Aus diesem Grund werden die Erkennungsergebnisse normalerweise nicht vom Gericht verabschiedet, obwohl es dazu geführt hat, dass viele unschuldige Menschen inhaftiert wurden. Im Gegensatz dazu ist künstliche Intelligenz eine leistungsstarke Datenmotor, und ihr Arbeitsprinzip besteht darin, alle Aspekte zu beobachten. Dies bedeutet, dass Wissenschaftler künstliche Intelligenz auf Anwendungen anwenden können, die auf verschiedene Weise Wahrheit suchen. Ein Ansatz besteht darin, die Vitalzeichenreaktionen der Person zu analysieren, die wie ein Lügendetektor befragt wird, jedoch mit einer detaillierteren und präziseren vergleichenden Analyse. Ein anderer Ansatz ist die Verwendung von Sprachmarkup, um zu analysieren, was Menschen tatsächlich sagen und Logik und Argumentation verwenden. Wie das Sprichwort sagt, züchtet eine Lüge eine andere Lüge und schließlich
 Wird die KI für den Start in der Luft- und Raumfahrtindustrie geklärt?Apr 28, 2025 am 11:10 AM
Wird die KI für den Start in der Luft- und Raumfahrtindustrie geklärt?Apr 28, 2025 am 11:10 AMDie Luft- und Raumfahrtindustrie, ein Pionier der Innovation, nutzt KI, um ihre komplizierten Herausforderungen zu bewältigen. Die zunehmende Komplexität der Modern Aviation erfordert die Automatisierung und Echtzeit-Intelligenzfunktionen von KI für verbesserte Sicherheit, reduzierter Oper
 Beobachten Sie das Frühling -Roboter -Rennen von PekingApr 28, 2025 am 11:09 AM
Beobachten Sie das Frühling -Roboter -Rennen von PekingApr 28, 2025 am 11:09 AMDie schnelle Entwicklung der Robotik hat uns eine faszinierende Fallstudie gebracht. Der N2 -Roboter von Noetix wiegt über 40 Pfund und ist 3 Fuß groß und soll in der Lage sein, sich zurückzufassen. Der G1 -Roboter von Unitree wiegt etwa doppelt so groß wie der N2 und ist etwa 4 Fuß hoch. Es gibt auch viele kleinere humanoide Roboter, die am Wettbewerb teilnehmen, und es gibt sogar einen Roboter, der von einem Fan vorangetrieben wird. Dateninterpretation Der Halbmarathon zog mehr als 12.000 Zuschauer an, aber nur 21 humanoide Roboter nahmen teil. Obwohl die Regierung darauf hinwies, dass die teilnehmenden Roboter vor dem Wettbewerb eine "intensive Ausbildung" durchführten, haben nicht alle Roboter den gesamten Wettbewerb abgeschlossen. Champion - Tiangong ult entwickelt vom Peking Humanoiden Roboter Innovation Center
 Die Spiegelfalle: AI -Ethik und der Zusammenbruch der menschlichen VorstellungskraftApr 28, 2025 am 11:08 AM
Die Spiegelfalle: AI -Ethik und der Zusammenbruch der menschlichen VorstellungskraftApr 28, 2025 am 11:08 AMKünstliche Intelligenz in ihrer aktuellen Form ist nicht wirklich intelligent. Es ist geschickt darin, vorhandene Daten nachzuahmen und zu verfeinern. Wir schaffen keine künstliche Intelligenz, sondern künstliche Schluss
 Neues Google Leak enthüllt praktische Google -Fotos -Funktionen UpdateApr 28, 2025 am 11:07 AM
Neues Google Leak enthüllt praktische Google -Fotos -Funktionen UpdateApr 28, 2025 am 11:07 AMIn einem Bericht wurde festgestellt, dass eine aktualisierte Schnittstelle im Code für Google Photos Android Version 7.26 versteckt wurde. Bei jedem Anzeigen eines Fotos werden am unteren Bildschirmrand eine Reihe neu erkannter Vorschaubildesansichten angezeigt. In den neuen Miniaturansichten des Gesichts fehlen Namensschilds. Ich vermute daher, dass Sie einzeln auf sie klicken müssen, um weitere Informationen zu jeder erkannten Person anzuzeigen. Im Moment bietet diese Funktion keine anderen Informationen als diejenigen, die Google Photos in Ihren Bildern gefunden haben. Diese Funktion ist noch nicht verfügbar, daher wissen wir nicht, wie Google sie genau verwendet. Google kann Miniaturansichten verwenden, um mehr Fotos von ausgewählten Personen zu finden, oder kann für andere Zwecke verwendet werden, z. B. für die Bearbeitung der Person. Lassen Sie uns warten und sehen. Wie vorerst
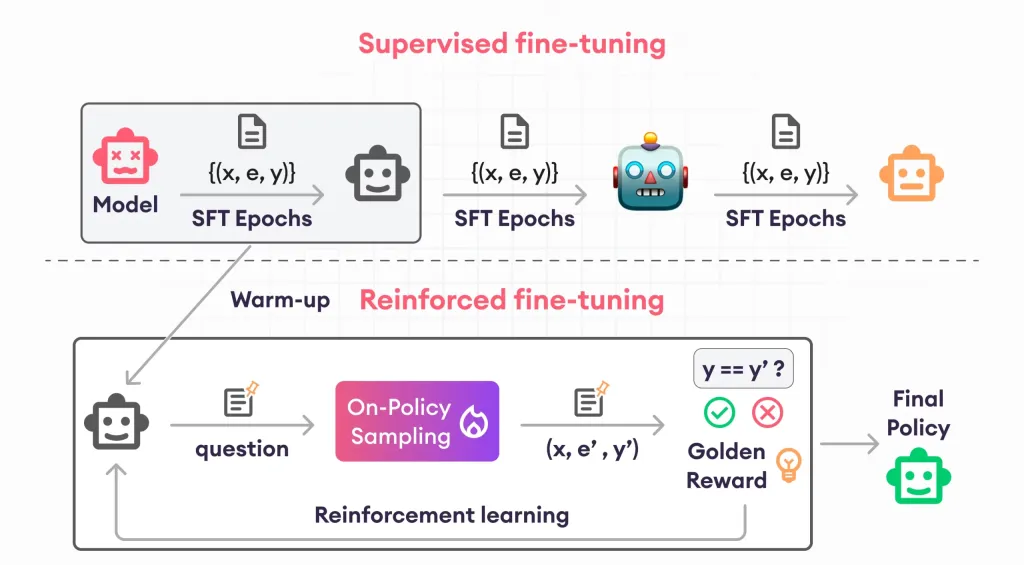 Leitfaden zur Verstärkungsfonetuning - Analytics VidhyaApr 28, 2025 am 09:30 AM
Leitfaden zur Verstärkungsfonetuning - Analytics VidhyaApr 28, 2025 am 09:30 AMDie Verstärkungsfonetuning hat die KI -Entwicklung erschüttert, indem sie Modelle unterrichten, um sich auf der Grundlage des menschlichen Feedbacks anzupassen. Es mischt beaufsichtigte Lernfundamente mit belohnungsbasierten Updates, um sie sicherer, genauerer und wirklich hilfreicher zu machen
 Lassen Sie uns tanzen: Strukturierte Bewegung, um unsere menschlichen neuronalen Netze zu optimierenApr 27, 2025 am 11:09 AM
Lassen Sie uns tanzen: Strukturierte Bewegung, um unsere menschlichen neuronalen Netze zu optimierenApr 27, 2025 am 11:09 AMWissenschaftler haben ausführlich menschliche und einfachere neuronale Netzwerke (wie die in C. elegans) untersucht, um ihre Funktionalität zu verstehen. Es stellt sich jedoch eine entscheidende Frage: Wie passen wir unsere eigenen neuronalen Netze an, um neben neuartigen Ai S effektiv zu arbeiten


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

mPDF
mPDF ist eine PHP-Bibliothek, die PDF-Dateien aus UTF-8-codiertem HTML generieren kann. Der ursprüngliche Autor, Ian Back, hat mPDF geschrieben, um PDF-Dateien „on the fly“ von seiner Website auszugeben und verschiedene Sprachen zu verarbeiten. Es ist langsamer und erzeugt bei der Verwendung von Unicode-Schriftarten größere Dateien als Originalskripte wie HTML2FPDF, unterstützt aber CSS-Stile usw. und verfügt über viele Verbesserungen. Unterstützt fast alle Sprachen, einschließlich RTL (Arabisch und Hebräisch) und CJK (Chinesisch, Japanisch und Koreanisch). Unterstützt verschachtelte Elemente auf Blockebene (wie P, DIV),

Dreamweaver CS6
Visuelle Webentwicklungstools

WebStorm-Mac-Version
Nützliche JavaScript-Entwicklungstools

Sicherer Prüfungsbrowser
Safe Exam Browser ist eine sichere Browserumgebung für die sichere Teilnahme an Online-Prüfungen. Diese Software verwandelt jeden Computer in einen sicheren Arbeitsplatz. Es kontrolliert den Zugriff auf alle Dienstprogramme und verhindert, dass Schüler nicht autorisierte Ressourcen nutzen.






