
Beim maschinellen Lernen sind Matrixoperationen ein wichtiges mathematisches Werkzeug zur Verarbeitung und Transformation von Daten. Durch die Darstellung von Daten in Matrixform können Sie verschiedene lineare Algebraoperationen wie Matrixmultiplikationen, Additionen und Umkehroperationen durchführen. Diese Operationen können zur Merkmalstransformation, Parameteroptimierung und Vorhersageberechnungen während des Modelltrainings und der Inferenz verwendet werden. Durch Matrixoperationen können wir große Datensätze effektiv verarbeiten und die Vorteile paralleler Berechnungen nutzen, um den Berechnungsprozess zu beschleunigen. Darüber hinaus stehen Matrixoperationen in engem Zusammenhang mit Bereichen wie Merkmalsextraktion, Dimensionsreduktion und Bildverarbeitung und bieten eine leistungsstarke mathematische Grundlage und Werkzeuge für maschinelles Lernen.
Matrixoperationen werden häufig beim maschinellen Lernen eingesetzt. Im Folgenden werden einige gängige Anwendungsszenarien ausführlich vorgestellt.
1. Lineare Regression
Die lineare Regression ist ein maschineller Lernalgorithmus, der verwendet wird, um lineare Beziehungen zwischen Variablen herzustellen. Es passt den Unterschied zwischen Datenpunkten und einem linearen Modell an, indem es eine Zielfunktion minimiert. Typischerweise verwendet die Zielfunktion den mittleren quadratischen Fehler, um den Grad der Anpassung zu messen. Um die Regressionskoeffizienten zu ermitteln und Vorhersagen zu treffen, können Matrixoperationen mit Methoden wie Normalgleichungen oder Gradientenabstieg durchgeführt werden.
2. Hauptkomponentenanalyse (PCA)
Die Hauptkomponentenanalyse ist eine häufig verwendete Technik zur Dimensionsreduktion, mit der die wichtigsten Merkmale aus hochdimensionalen Datensätzen extrahiert werden. PCA ordnet die Originaldaten einem neuen Merkmalsraum zu, sodass die Korrelation zwischen den neuen Merkmalen minimal ist. Dieser Abbildungsprozess umfasst die Eigenwertzerlegung der Datenkovarianzmatrix und die Auswahl des Eigenvektors, der dem größten Eigenwert entspricht, als Hauptkomponente. Durch Matrixoperationen kann der PCA-Algorithmus effektiv implementiert werden.
3. Neuronales Netzwerk
Neuronales Netzwerk ist ein Modell für maschinelles Lernen, das die Arbeitsweise von Neuronen im menschlichen Gehirn simuliert. Neuronale Netze bestehen normalerweise aus mehreren Neuronenschichten, wobei jedes Neuron mit allen Neuronen der nächsten Schicht verbunden ist. In neuronalen Netzen werden Eingaben und Gewichte als Matrizen dargestellt und Informationen werden durch eine Kombination aus Matrixmultiplikation und nichtlinearen Aktivierungsfunktionen übertragen und transformiert. Matrixoperationen spielen in neuronalen Netzen eine wichtige Rolle. Sie werden zur Berechnung der Eingabe und Ausgabe jedes Neurons sowie zur Aktualisierung von Netzwerkparametern (Gewichtungen und Bias) verwendet.
4. Bildverarbeitung
Bildverarbeitung ist ein weiteres wichtiges Anwendungsfeld im maschinellen Lernen. Bilder werden normalerweise als Matrix von Pixelwerten dargestellt. Durch die Durchführung von Matrixoperationen an Bildmatrizen können verschiedene Bildverarbeitungsaufgaben erreicht werden, z. B. Bildfilterung, Kantenerkennung, Bildverbesserung usw. Gängige Bildverarbeitungstechniken wie Faltungs-Neuronale Netze nutzen Faltungsoperationen, um Bilder zu extrahieren und zu klassifizieren.
5. Empfehlungssystem
Das Empfehlungssystem ist eine Schlüsseltechnologie, die Benutzern hilft, personalisierte Interessen zu entdecken. Auf Matrixoperationen basierende Empfehlungssysteme werden häufig verwendet, um die Interaktion zwischen Benutzern und Elementen zu analysieren und Elemente vorherzusagen, an denen der Benutzer interessiert sein könnte. Durch die Darstellung von Benutzerbewertungen oder Verhaltensdatensätzen als Matrizen können Methoden wie die Matrixfaktorisierung verwendet werden, um versteckte Merkmale zwischen Benutzern und Elementen abzuleiten und personalisierte Empfehlungen bereitzustellen.
Zusammenfassend lässt sich sagen, dass Matrixoperationen beim maschinellen Lernen in zahlreichen Anwendungsszenarien eine wichtige Rolle spielen. Sie können hochdimensionale Daten effektiv verarbeiten, Merkmale extrahieren, Modellparameter optimieren und komplexe Datentransformations- und Vorhersageaufgaben implementieren. Durch den Einsatz von Matrixoperationen können wir Daten besser verstehen und nutzen und genauere und effektivere Modelle für maschinelles Lernen erstellen.
Das obige ist der detaillierte Inhalt vonMatrixberechnung und Praxis im maschinellen Lernen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Lesen des AI-Index 2025: Ist AI Ihr Freund, Feind oder Co-Pilot?Apr 11, 2025 pm 12:13 PM
Lesen des AI-Index 2025: Ist AI Ihr Freund, Feind oder Co-Pilot?Apr 11, 2025 pm 12:13 PMDer Bericht des Stanford University Institute for Human-orientierte künstliche Intelligenz bietet einen guten Überblick über die laufende Revolution der künstlichen Intelligenz. Interpretieren wir es in vier einfachen Konzepten: Erkenntnis (verstehen, was geschieht), Wertschätzung (Sehenswürdigkeiten), Akzeptanz (Gesichtsherausforderungen) und Verantwortung (finden Sie unsere Verantwortlichkeiten). Kognition: Künstliche Intelligenz ist überall und entwickelt sich schnell Wir müssen uns sehr bewusst sein, wie schnell künstliche Intelligenz entwickelt und ausbreitet. Künstliche Intelligenzsysteme verbessern sich ständig und erzielen hervorragende Ergebnisse bei mathematischen und komplexen Denktests, und erst vor einem Jahr haben sie in diesen Tests kläglich gescheitert. Stellen Sie sich vor, KI zu lösen komplexe Codierungsprobleme oder wissenschaftliche Probleme auf Graduiertenebene-seit 2023-
 Erste Schritte mit Meta Lama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PM
Erste Schritte mit Meta Lama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PMMetas Lama 3.2: Ein Sprung nach vorne in der multimodalen und mobilen KI Meta hat kürzlich Lama 3.2 vorgestellt, ein bedeutender Fortschritt in der KI mit leistungsstarken Sichtfunktionen und leichten Textmodellen, die für mobile Geräte optimiert sind. Aufbau auf dem Erfolg o
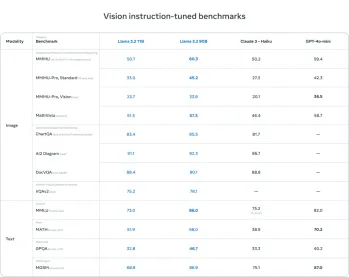 AV -Bytes: META ' S Lama 3.2, Googles Gemini 1.5 und mehrApr 11, 2025 pm 12:01 PM
AV -Bytes: META ' S Lama 3.2, Googles Gemini 1.5 und mehrApr 11, 2025 pm 12:01 PMDie KI -Landschaft dieser Woche: Ein Wirbelsturm von Fortschritten, ethischen Überlegungen und regulatorischen Debatten. Hauptakteure wie OpenAI, Google, Meta und Microsoft haben einen Strom von Updates veröffentlicht, von bahnbrechenden neuen Modellen bis hin zu entscheidenden Verschiebungen in LE
 Die menschlichen Kosten für das Gespräch mit Maschinen: Kann sich ein Chatbot wirklich darum kümmern?Apr 11, 2025 pm 12:00 PM
Die menschlichen Kosten für das Gespräch mit Maschinen: Kann sich ein Chatbot wirklich darum kümmern?Apr 11, 2025 pm 12:00 PMDie beruhigende Illusion der Verbindung: Blühen wir in unseren Beziehungen zur KI wirklich auf? Diese Frage stellte den optimistischen Ton des "Fortschritts -Menschen mit AI) des MIT Media Lab in Frage. Während die Veranstaltung moderne EDG präsentierte
 Verständnis der Scipy Library in PythonApr 11, 2025 am 11:57 AM
Verständnis der Scipy Library in PythonApr 11, 2025 am 11:57 AMEinführung Stellen Sie sich vor, Sie sind ein Wissenschaftler oder Ingenieur, der sich mit komplexen Problemen befasst - Differentialgleichungen, Optimierungsherausforderungen oder Fourier -Analysen. Pythons Benutzerfreundlichkeit und Grafikfunktionen sind ansprechend, aber diese Aufgaben erfordern leistungsstarke Tools
 3 Methoden zum Ausführen von LLAMA 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AM
3 Methoden zum Ausführen von LLAMA 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AMMETAs Lama 3.2: Ein multimodales KI -Kraftpaket Das neueste multimodale Modell von META, Lama 3.2, stellt einen erheblichen Fortschritt in der KI dar, das ein verbessertes Sprachverständnis, eine verbesserte Genauigkeit und die überlegenen Funktionen der Textgenerierung bietet. Seine Fähigkeit t
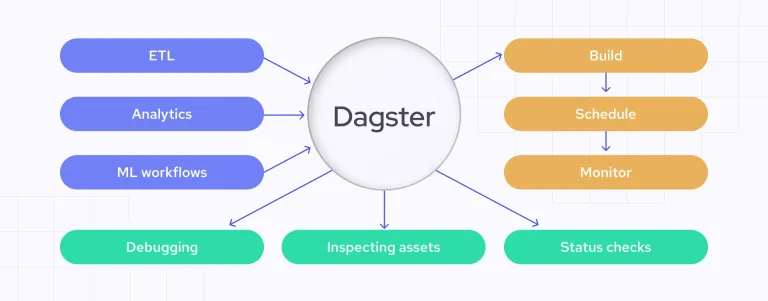 Automatisierung von Datenqualitätsprüfungen mit DagsterApr 11, 2025 am 11:44 AM
Automatisierung von Datenqualitätsprüfungen mit DagsterApr 11, 2025 am 11:44 AMDatenqualitätssicherung: Automatisieren von Schecks mit Dagster und großen Erwartungen Die Aufrechterhaltung einer hohen Datenqualität ist für datengesteuerte Unternehmen von entscheidender Bedeutung. Wenn Datenvolumina und Quellen zunehmen, wird die manuelle Qualitätskontrolle ineffizient und anfällig für Fehler.
 Haben Mainframes eine Rolle in der KI -Ära?Apr 11, 2025 am 11:42 AM
Haben Mainframes eine Rolle in der KI -Ära?Apr 11, 2025 am 11:42 AMMainframes: Die unbesungenen Helden der KI -Revolution Während die Server bei allgemeinen Anwendungen und mehreren Kunden übernommen werden, werden Mainframes für hochvolumige, missionskritische Aufgaben erstellt. Diese leistungsstarken Systeme sind häufig in Heavil gefunden


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Herunterladen der Mac-Version des Atom-Editors
Der beliebteste Open-Source-Editor

Dreamweaver CS6
Visuelle Webentwicklungstools

ZendStudio 13.5.1 Mac
Leistungsstarke integrierte PHP-Entwicklungsumgebung

EditPlus chinesische Crack-Version
Geringe Größe, Syntaxhervorhebung, unterstützt keine Code-Eingabeaufforderungsfunktion





