 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte KI
KI Anwendungen und Beispiele in der Bilderkennung und dem Prinzip des Fehler-Rückausbreitungsalgorithmus
Anwendungen und Beispiele in der Bilderkennung und dem Prinzip des Fehler-RückausbreitungsalgorithmusAnwendungen und Beispiele in der Bilderkennung und dem Prinzip des Fehler-Rückausbreitungsalgorithmus

Error Back Propagation ist ein häufig verwendeter Algorithmus für maschinelles Lernen und wird häufig beim Training neuronaler Netze, insbesondere im Bereich der Bilderkennung, eingesetzt. In diesem Artikel werden die Anwendung, Prinzipien und Beispiele dieses Algorithmus bei der Bilderkennung vorgestellt.
1. Anwendung des Fehler-Backpropagation-Algorithmus
Bilderkennung ist eine Methode, bei der mithilfe von Computerprogrammen Zahlen oder Bilder analysiert, verarbeitet und verstanden werden, um die darin enthaltenen Informationen und Merkmale zu identifizieren. Bei der Bilderkennung wird häufig der Fehler-Rückausbreitungsalgorithmus verwendet. Dieser Algorithmus löst die Erkennungsaufgabe durch Training eines neuronalen Netzwerks. Ein neuronales Netzwerk ist ein Rechenmodell, das die Interaktionen zwischen Neuronen im menschlichen Gehirn simuliert und in der Lage ist, komplexe Eingabedaten effizient zu verarbeiten und zu klassifizieren. Durch die kontinuierliche Anpassung der Gewichte und Bias des neuronalen Netzwerks ermöglicht der Fehler-Backpropagation-Algorithmus dem neuronalen Netzwerk, schrittweise zu lernen und seine Erkennungsfähigkeiten zu verbessern.
Der Fehlerrückausbreitungsalgorithmus minimiert den Fehler zwischen den Ausgabeergebnissen und den tatsächlichen Ergebnissen, indem er die Gewichte und Verzerrungen des neuronalen Netzwerks anpasst. Der Trainingsprozess besteht aus den folgenden Schritten: Berechnen der Ausgabe des neuronalen Netzwerks, Berechnen des Fehlers, Rückpropagieren des Fehlers an jedes Neuron und Anpassen der Gewichte und Verzerrungen basierend auf dem Fehler.
1. Initialisieren Sie die Gewichte und Verzerrungen des neuronalen Netzwerks zufällig.
2. Berechnen Sie die Ausgabe des neuronalen Netzwerks, indem Sie einen Satz Trainingsdaten eingeben.
3. Berechnen Sie den Fehler zwischen dem Ausgabeergebnis und dem tatsächlichen Ergebnis.
4. Propagieren Sie Fehler zurück und passen Sie die Gewichte und Verzerrungen des neuronalen Netzwerks an.
5. Wiederholen Sie die Schritte 2-4, bis der Fehler den Mindestwert erreicht oder die voreingestellten Trainingszeiten erreicht sind.
Der Trainingsprozess des Fehlerrückausbreitungsalgorithmus kann als Optimierungsproblem betrachtet werden, dh als Minimierung des Fehlers zwischen dem Ausgabeergebnis des neuronalen Netzwerks und dem tatsächlichen Ergebnis. Während des Trainingsprozesses passt der Algorithmus kontinuierlich die Gewichte und Bias des neuronalen Netzwerks an, sodass der Fehler allmählich abnimmt und letztendlich eine höhere Erkennungsgenauigkeit erreicht wird.
Die Anwendung des Fehlerrückausbreitungsalgorithmus ist nicht nur auf die Bilderkennung beschränkt, sondern kann auch in der Spracherkennung, der Verarbeitung natürlicher Sprache und anderen Bereichen eingesetzt werden. Durch die weit verbreitete Anwendung können viele Technologien der künstlichen Intelligenz effizienter implementiert werden.
2. Prinzip des Fehler-Rückausbreitungsalgorithmus
Das Prinzip des Fehler-Rückausbreitungsalgorithmus kann in den folgenden Schritten zusammengefasst werden:
1: Geben Sie ein Trainingsmuster ein und leiten Sie es durch das Neuron Netzwerk Der Vorwärtsdurchlauf des Netzwerks berechnet die Ausgabe.
2. Fehler berechnen: Vergleichen Sie das Ausgabeergebnis mit dem tatsächlichen Ergebnis und berechnen Sie den Fehler.
3. Backpropagation: Backpropagation des Fehlers von der Ausgabeschicht zur Eingabeschicht, wobei das Gewicht und die Vorspannung jedes Neurons angepasst werden.
4. Gewichte und Verzerrungen aktualisieren: Aktualisieren Sie basierend auf den durch Backpropagation erhaltenen Gradienteninformationen die Gewichte und Verzerrungen der Neuronen, um den Fehler in der nächsten Runde der Vorwärtsausbreitung zu verringern.
Im Fehler-Backpropagation-Algorithmus ist der Backpropagation-Prozess der Schlüssel. Es leitet den Fehler über die Kettenregel von der Ausgabeschicht an die Eingabeschicht weiter, berechnet den Beitrag jedes Neurons zum Fehler und passt die Gewichte und Verzerrungen entsprechend dem Grad des Beitrags an. Konkret kann die Kettenregel durch die folgende Formel ausgedrückt werden:
frac{partial E}{partial w_{i,j}}=frac{partial E}{partial y_j}frac{partial y_j}{partial z_j } frac{partial z_j}{partial w_{i,j}}
wobei E den Fehler darstellt, w_{i,j} das Gewicht darstellt, das das i-te Neuron und das j-te Neuron verbindet, y_j das darstellt Die Ausgabe von j Neuronen, z_j, repräsentiert die gewichtete Summe des j-ten Neurons. Diese Formel kann so erklärt werden, dass sich die Auswirkung des Fehlers auf das Verbindungsgewicht aus dem Produkt der Ausgabe y_j, der Ableitung der Aktivierungsfunktion frac{partial y_j}{partial z_j} und der Eingabe x_i zusammensetzt.
Durch die Kettenregel kann der Fehler auf jedes Neuron zurückpropagiert werden und der Beitrag jedes Neurons zum Fehler wird berechnet. Anschließend werden die Gewichte und Bias entsprechend dem Grad des Beitrags angepasst, sodass der Fehler in der nächsten Runde der Vorwärtsausbreitung kleiner wird.
3. Beispiel eines Fehler-Rückausbreitungsalgorithmus
Das Folgende ist ein einfaches Beispiel, um zu veranschaulichen, wie der Fehler-Rückausbreitungsalgorithmus auf die Bilderkennung angewendet wird.
Angenommen, wir haben ein 28x28 großes Bild handgeschriebener Ziffern und möchten ein neuronales Netzwerk verwenden, um diese Zahl zu erkennen. Wir erweitern dieses Bild in einen 784-dimensionalen Vektor und verwenden jedes Pixel als Eingabe für das neuronale Netzwerk.
Wir nutzen für das Training ein neuronales Netzwerk mit zwei versteckten Schichten. Jede verborgene Schicht verfügt über 64 Neuronen und die Ausgabeschicht über 10 Neuronen, die jeweils die Zahlen 0–9 darstellen.
Zuerst initialisieren wir zufällig die Gewichte und Bias des neuronalen Netzwerks. Anschließend geben wir einen Satz Trainingsdaten ein und berechnen die Ausgabe durch Vorwärtsausbreitung. Angenommen, das Ausgabeergebnis ist [0,1,0,2,0,05,0,3,0,02,0,15,0,05,0,1,0,03,0,1], was bedeutet, dass das neuronale Netzwerk davon ausgeht, dass es sich bei diesem Bild höchstwahrscheinlich um die Zahl 3 handelt.
Als nächstes berechnen wir den Fehler zwischen dem Ausgabeergebnis und dem tatsächlichen Ergebnis. Angenommen, das tatsächliche Ergebnis ist [0,0,0,1,0,0,0,0,0,0], was bedeutet, dass die tatsächliche Anzahl dieses Bildes 3 ist. Wir können die Kreuzentropieverlustfunktion verwenden, um den Fehler zu berechnen. Die Formel lautet wie folgt:
E=-sum_{i=1}^{10}y_i log(p_i)
Unter diesen repräsentiert y_i das i-te Element des tatsächlichen Ergebnisses und p_i repräsentiert das i-te Element des Ausgabeergebnisses des neuronalen Netzwerks. Setzt man die tatsächlichen Ergebnisse und die Ausgabe des neuronalen Netzwerks in die Formel ein, beträgt der Fehler 0,356.
Als nächstes übertragen wir den Fehler zurück in das neuronale Netzwerk, berechnen den Beitrag jedes Neurons zum Fehler und passen die Gewichte und Verzerrungen basierend auf dem Grad des Beitrags an. Wir können den Gradientenabstiegsalgorithmus verwenden, um die Gewichte und Verzerrungen zu aktualisieren. Die Formel lautet wie folgt:
w_{i,j}=w_{i,j}-alphafrac{partial E}{partial w_{i,j }}
Dabei stellt Alpha die Lernrate dar, mit der die Schrittgröße jedes Updates angepasst wird. Durch kontinuierliche Anpassung der Gewichte und Verzerrungen können wir die Ausgabeergebnisse des neuronalen Netzwerks den tatsächlichen Ergebnissen näher bringen und so die Erkennungsgenauigkeit verbessern.
Das Obige ist die Anwendung, das Prinzip und das Beispiel eines Fehlerrückausbreitungsalgorithmus bei der Bilderkennung. Der Fehler-Rückausbreitungsalgorithmus passt die Gewichte und Verzerrungen des neuronalen Netzwerks kontinuierlich an, sodass das neuronale Netzwerk Bilder genauer identifizieren kann und breite Anwendungsaussichten hat.
Das obige ist der detaillierte Inhalt vonAnwendungen und Beispiele in der Bilderkennung und dem Prinzip des Fehler-Rückausbreitungsalgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Die KI -Kompetenzlücke verlangsamt die VersorgungskettenApr 26, 2025 am 11:13 AM
Die KI -Kompetenzlücke verlangsamt die VersorgungskettenApr 26, 2025 am 11:13 AMDer Begriff "AI-fähige Belegschaft" wird häufig verwendet, aber was bedeutet das in der Lieferkettenindustrie wirklich? Nach Abe Eshkenazi, CEO des Association for Supply Chain Management (ASCM), bedeutet dies Fachkräfte, die kritisch sind
 Wie ein Unternehmen leise daran arbeitet, die KI für immer zu verwandelnApr 26, 2025 am 11:12 AM
Wie ein Unternehmen leise daran arbeitet, die KI für immer zu verwandelnApr 26, 2025 am 11:12 AMDie dezentrale KI -Revolution gewinnt leise an Dynamik. An diesem Freitag in Austin, Texas, markiert der Bittensor Endgame Summit einen entscheidenden Moment, in dem die dezentrale KI (DEAI) von Theorie zu praktischer Anwendung übergeht. Im Gegensatz zum glitzernden Werbespot
 Nvidia veröffentlicht Nemo Microservices, um die Entwicklung der AI -Agenten zu optimierenApr 26, 2025 am 11:11 AM
Nvidia veröffentlicht Nemo Microservices, um die Entwicklung der AI -Agenten zu optimierenApr 26, 2025 am 11:11 AMEnterprise KI steht vor der Datenintegrationsprobleme Die Anwendung von Enterprise KI steht vor einer großen Herausforderung: Aufbau von Systemen, die die Genauigkeit und Praktikabilität durch kontinuierlich lernende Geschäftsdaten aufrechterhalten können. NEMO Microservices lösen dieses Problem, indem er das erstellt, was NVIDIA als "Datenschwungrad" beschreibt und KI -Systemen durch kontinuierliche Exposition gegenüber Unternehmensinformationen und Benutzerinteraktion relevant bleibt. Dieses neu gestartete Toolkit enthält fünf wichtige Microservices: Nemo Customizer behandelt die Feinabstimmung großer Sprachmodelle mit höherem Trainingsdurchsatz. NEMO Evaluator bietet eine vereinfachte Bewertung von KI -Modellen für benutzerdefinierte Benchmarks. NEMO -Leitplanken implementiert Sicherheitskontrollen, um die Einhaltung und Angemessenheit aufrechtzuerhalten
 KI malt ein neues Bild für die Zukunft von Kunst und DesignApr 26, 2025 am 11:10 AM
KI malt ein neues Bild für die Zukunft von Kunst und DesignApr 26, 2025 am 11:10 AMAI: Die Zukunft von Kunst und Design Künstliche Intelligenz (KI) verändert das Kunst- und Designgebiet auf beispiellose Weise, und seine Auswirkungen beschränken sich nicht mehr auf Amateure, sondern beeinflussen jedoch die Fachkräfte. Kunstwerke und Designschemata, die von KI erzeugt wurden, ersetzen traditionelle materielle Bilder und Designer in vielen Transaktionsdesignaktivitäten wie Werbung, Social -Media -Bildgenerierung und Webdesign schnell. Professionelle Künstler und Designer finden jedoch auch den praktischen Wert von KI. Sie verwenden AI als Hilfsmittel, um neue ästhetische Möglichkeiten zu erforschen, verschiedene Stile zu mischen und neuartige visuelle Effekte zu erzeugen. KI hilft Künstlern und Designer, sich wiederholende Aufgaben zu automatisieren, verschiedene Designelemente vorzuschlagen und kreative Eingaben zu leisten. AI unterstützt den Stiltransfer, der einen Bildstil anwenden soll
 Wie Zoom die Arbeit mit Agentic AI: Von Meetings bis Meilensteinen revolutioniertApr 26, 2025 am 11:09 AM
Wie Zoom die Arbeit mit Agentic AI: Von Meetings bis Meilensteinen revolutioniertApr 26, 2025 am 11:09 AMZoom, ursprünglich für seine Video -Konferenz -Plattform bekannt, führt eine Revolution am Arbeitsplatz mit der innovativen Nutzung der Agenten -KI. Ein aktuelles Gespräch mit Zooms CTO, XD Huang, enthüllte die ehrgeizige Vision des Unternehmens. Definieren von Agenten AI Huang d
 Die existenzielle Bedrohung für UniversitätenApr 26, 2025 am 11:08 AM
Die existenzielle Bedrohung für UniversitätenApr 26, 2025 am 11:08 AMWird AI die Bildung revolutionieren? Diese Frage führt zu ernsthafter Reflexion unter Pädagogen und Stakeholdern. Die Integration von KI in Bildung bietet sowohl Chancen als auch Herausforderungen. Wie Matthew Lynch von The Tech Edvocate bemerkt, Universität
 Der Prototyp: Amerikanische Wissenschaftler suchen nach Jobs im AuslandApr 26, 2025 am 11:07 AM
Der Prototyp: Amerikanische Wissenschaftler suchen nach Jobs im AuslandApr 26, 2025 am 11:07 AMDie Entwicklung wissenschaftlicher Forschung und Technologie in den Vereinigten Staaten kann vor Herausforderungen stehen, möglicherweise aufgrund von Budgetkürzungen. Nach der Natur stieg die Zahl der amerikanischen Wissenschaftler, die sich für Arbeitsplätze in Übersee bewerben, von Januar bis März 2025 im Vergleich zum gleichen Zeitraum von 2024 um 32%. Eine frühere Umfrage ergab, dass 75% der untersuchten Forscher über die Suche nach Arbeitsplätzen in Europa und Kanada in Betracht gezogen wurden. In den letzten Monaten wurden Hunderte von NIH- und NSF-Zuschüssen beendet, wobei die neuen Zuschüsse von NIH in diesem Jahr um etwa 2,3 Milliarden US-Dollar gesunken sind, ein Rückgang von fast einem Drittel. Der durchgesickerte Haushaltsvorschlag zeigt, dass die Trump -Administration mit einer möglichen Reduzierung von um bis zu 50%ein starkes Budget für wissenschaftliche Institutionen in Betracht zieht. Die Turbulenzen auf dem Gebiet der Grundlagenforschung haben sich auch auf einen der Hauptvorteile der Vereinigten Staaten ausgewirkt: die Gewinnung von Talenten in Übersee. 35
 Alles über Open AIs neueste GPT 4.1 -Familie - Analytics VidhyaApr 26, 2025 am 10:19 AM
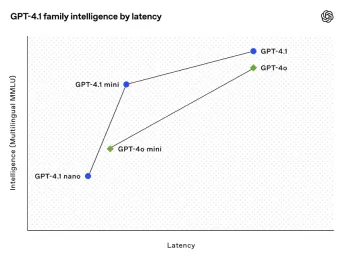
Alles über Open AIs neueste GPT 4.1 -Familie - Analytics VidhyaApr 26, 2025 am 10:19 AMOpenAI enthüllt die leistungsstarke GPT-4.1-Serie: eine Familie von drei fortschrittlichen Sprachmodellen für reale Anwendungen. Dieser signifikante Sprung nach vorne bietet schnellere Reaktionszeiten, verbessertes Verständnis und drastisch reduzierte Kosten im Vergleich t t


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

Video Face Swap
Tauschen Sie Gesichter in jedem Video mühelos mit unserem völlig kostenlosen KI-Gesichtstausch-Tool aus!

Heißer Artikel

Heiße Werkzeuge

Sicherer Prüfungsbrowser
Safe Exam Browser ist eine sichere Browserumgebung für die sichere Teilnahme an Online-Prüfungen. Diese Software verwandelt jeden Computer in einen sicheren Arbeitsplatz. Es kontrolliert den Zugriff auf alle Dienstprogramme und verhindert, dass Schüler nicht autorisierte Ressourcen nutzen.

Notepad++7.3.1
Einfach zu bedienender und kostenloser Code-Editor

SAP NetWeaver Server-Adapter für Eclipse
Integrieren Sie Eclipse mit dem SAP NetWeaver-Anwendungsserver.

SublimeText3 chinesische Version
Chinesische Version, sehr einfach zu bedienen

EditPlus chinesische Crack-Version
Geringe Größe, Syntaxhervorhebung, unterstützt keine Code-Eingabeaufforderungsfunktion






