 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte KI
KI Theorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen
Theorie und Techniken der Gewichtsaktualisierung in neuronalen NetzenTheorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen

Die Gewichtsaktualisierung im neuronalen Netzwerk besteht darin, die Verbindungsgewichte zwischen Neuronen im Netzwerk mithilfe von Methoden wie dem Backpropagation-Algorithmus anzupassen, um die Leistung des Netzwerks zu verbessern. In diesem Artikel werden das Konzept und die Methode der Gewichtsaktualisierung vorgestellt, um den Lesern ein besseres Verständnis des Trainingsprozesses neuronaler Netze zu ermöglichen.
1. Konzept
Die Gewichte in neuronalen Netzen sind Parameter, die verschiedene Neuronen verbinden und die Stärke der Signalübertragung bestimmen. Jedes Neuron empfängt das Signal von der vorherigen Schicht, multipliziert es mit dem Gewicht der Verbindung, fügt einen Bias-Term hinzu und wird schließlich durch die Aktivierungsfunktion aktiviert und an die nächste Schicht weitergeleitet. Daher wirkt sich die Größe des Gewichts direkt auf die Stärke und Richtung des Signals aus, was wiederum Auswirkungen auf die Ausgabe des neuronalen Netzwerks hat.
Der Zweck der Gewichtsaktualisierung besteht darin, die Leistung des neuronalen Netzwerks zu optimieren. Während des Trainingsprozesses passt sich das neuronale Netzwerk an die Trainingsdaten an, indem es die Gewichte zwischen den Neuronen kontinuierlich anpasst, um die Vorhersagefähigkeit der Testdaten zu verbessern. Durch die Anpassung der Gewichte kann das neuronale Netzwerk die Trainingsdaten besser anpassen und dadurch die Vorhersagegenauigkeit verbessern. Auf diese Weise kann das neuronale Netzwerk die Ergebnisse unbekannter Daten genauer vorhersagen und eine bessere Leistung erzielen.
2. Methode
Zu den häufig verwendeten Methoden zur Gewichtsaktualisierung in neuronalen Netzen gehören Gradientenabstieg, stochastischer Gradientenabstieg und Batch-Gradientenabstieg.
Gradientenabstiegsmethode
Die Gradientenabstiegsmethode ist eine der grundlegendsten Methoden zur Gewichtsaktualisierung. Ihre Grundidee besteht darin, das Gewicht durch Berechnung des Gradienten der Verlustfunktion zum Gewicht (d. h. der Ableitung von) zu aktualisieren die Verlustfunktion zum Gewicht), um die Verlustfunktion zu minimieren. Konkret sind die Schritte der Gradientenabstiegsmethode wie folgt:
Zuerst müssen wir eine Verlustfunktion definieren, um die Leistung des neuronalen Netzwerks anhand der Trainingsdaten zu messen. Normalerweise wählen wir den mittleren quadratischen Fehler (MSE) als Verlustfunktion, der wie folgt definiert ist:
MSE=frac{1}{n}sum_{i=1}^{n}(y_i-hat {y_i })^2
wobei y_i den wahren Wert der i-ten Stichprobe darstellt, hat{y_i} den vom neuronalen Netzwerk vorhergesagten Wert der i-ten Stichprobe darstellt und n die Gesamtzahl darstellt Proben.
Dann müssen wir die Ableitung der Verlustfunktion nach dem Gewicht, also dem Gradienten, berechnen. Insbesondere kann für jedes Gewicht w_{ij} im neuronalen Netzwerk sein Gradient mit der folgenden Formel berechnet werden:
frac{partial MSE}{partial w_{ij}}=frac{2}{n}sum_ { k=1}^{n}(y_k-hat{y_k})cdot f'(sum_{j=1}^{m}w_{ij}x_{kj})cdot x_{ki}
wo , n stellt die Gesamtzahl der Stichproben dar, m stellt die Eingabeschichtgröße des neuronalen Netzwerks dar, x_{kj} stellt das j-te Eingabemerkmal der k-ten Stichprobe dar, f(cdot) stellt die Aktivierungsfunktion dar und f'( cdot) stellt die Ableitung der Aktivierungsfunktion dar.
Schließlich können wir die Gewichte durch die folgende Formel aktualisieren:
w_{ij}=w_{ij}-alphacdotfrac{partial MSE}{partial w_{ij}}
wobei Alpha Lernen darstellt Rate, steuert die Schrittgröße der Gewichtsaktualisierung.
Stochastische Gradientenabstiegsmethode
Die stochastische Gradientenabstiegsmethode ist eine Variante der Gradientenabstiegsmethode. Ihre Grundidee besteht darin, jedes Mal zufällig eine Stichprobe auszuwählen, um den Gradienten zu berechnen und die Gewichte zu aktualisieren. Im Vergleich zur Gradientenabstiegsmethode kann die stochastische Gradientenabstiegsmethode bei der Verarbeitung großer Datensätze schneller konvergieren und effizienter sein. Konkret sind die Schritte der stochastischen Gradientenabstiegsmethode wie folgt:
Zuerst müssen wir die Trainingsdaten mischen und zufällig eine Stichprobe x_k auswählen, um den Gradienten zu berechnen. Dann können wir die Ableitung der Verlustfunktion in Bezug auf das Gewicht mit der folgenden Formel berechnen:
frac{partial MSE}{partial w_{ij}}=2(y_k-hat{y_k})cdot f' (sum_{j= 1}^{m}w_{ij}x_{kj})cdot x_{ki}
wobei y_k den wahren Wert der k-ten Stichprobe darstellt und hat{y_k} den Vorhersage der k-ten Stichprobe durch den Wert des neuronalen Netzwerks.
Schließlich können wir die Gewichte durch die folgende Formel aktualisieren:
w_{ij}=w_{ij}-alphacdotfrac{partial MSE}{partial w_{ij}}
wobei Alpha darstellt Lernrate, steuert die Schrittgröße der Gewichtsaktualisierung.
Batch-Gradientenabstiegsmethode
Die Batch-Gradientenabstiegsmethode ist eine weitere Variante der Gradientenabstiegsmethode. Ihre Grundidee besteht darin, jedes Mal eine kleine Menge Proben zu verwenden, um den Gradienten zu berechnen und die Gewichte zu aktualisieren. Im Vergleich zur Gradientenabstiegsmethode und der stochastischen Gradientenabstiegsmethode kann die Batch-Gradientenabstiegsmethode stabiler konvergieren und ist bei der Verarbeitung kleiner Datensätze effizienter. Konkret sind die Schritte der Batch-Gradienten-Abstiegsmethode wie folgt:
Zuerst müssen wir die Trainingsdaten in mehrere Mini-Batches gleicher Größe aufteilen, wobei jeder Mini-Batch b Proben enthält. Wir können dann den durchschnittlichen Gradienten der Verlustfunktion gegenüber den Gewichten auf jedem Mini-Batch berechnen, der lautet:
frac{1}{b}sum_{k=1}^{b}frac{partial MSE}{ partiell w_ {ij}}
wobei b die Mini-Batch-Größe darstellt. Schließlich können wir die Gewichte mit der folgenden Formel aktualisieren:
w_{ij}=w_{ij}-alphacdotfrac{1}{b}sum_{k=1}^{b}frac{partial MSE}{partial w_ {ij}}
Dabei stellt Alpha die Lernrate dar, die die Schrittgröße der Gewichtsaktualisierung steuert.
Das obige ist der detaillierte Inhalt vonTheorie und Techniken der Gewichtsaktualisierung in neuronalen Netzen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Lesen des AI-Index 2025: Ist AI Ihr Freund, Feind oder Co-Pilot?Apr 11, 2025 pm 12:13 PM
Lesen des AI-Index 2025: Ist AI Ihr Freund, Feind oder Co-Pilot?Apr 11, 2025 pm 12:13 PMDer Bericht des Stanford University Institute for Human-orientierte künstliche Intelligenz bietet einen guten Überblick über die laufende Revolution der künstlichen Intelligenz. Interpretieren wir es in vier einfachen Konzepten: Erkenntnis (verstehen, was geschieht), Wertschätzung (Sehenswürdigkeiten), Akzeptanz (Gesichtsherausforderungen) und Verantwortung (finden Sie unsere Verantwortlichkeiten). Kognition: Künstliche Intelligenz ist überall und entwickelt sich schnell Wir müssen uns sehr bewusst sein, wie schnell künstliche Intelligenz entwickelt und ausbreitet. Künstliche Intelligenzsysteme verbessern sich ständig und erzielen hervorragende Ergebnisse bei mathematischen und komplexen Denktests, und erst vor einem Jahr haben sie in diesen Tests kläglich gescheitert. Stellen Sie sich vor, KI zu lösen komplexe Codierungsprobleme oder wissenschaftliche Probleme auf Graduiertenebene-seit 2023-
 Erste Schritte mit Meta Lama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PM
Erste Schritte mit Meta Lama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PMMetas Lama 3.2: Ein Sprung nach vorne in der multimodalen und mobilen KI Meta hat kürzlich Lama 3.2 vorgestellt, ein bedeutender Fortschritt in der KI mit leistungsstarken Sichtfunktionen und leichten Textmodellen, die für mobile Geräte optimiert sind. Aufbau auf dem Erfolg o
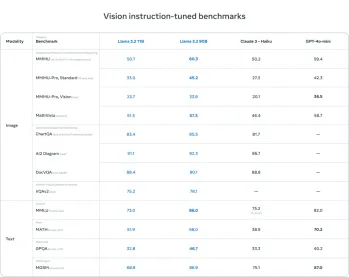 AV -Bytes: META ' S Lama 3.2, Googles Gemini 1.5 und mehrApr 11, 2025 pm 12:01 PM
AV -Bytes: META ' S Lama 3.2, Googles Gemini 1.5 und mehrApr 11, 2025 pm 12:01 PMDie KI -Landschaft dieser Woche: Ein Wirbelsturm von Fortschritten, ethischen Überlegungen und regulatorischen Debatten. Hauptakteure wie OpenAI, Google, Meta und Microsoft haben einen Strom von Updates veröffentlicht, von bahnbrechenden neuen Modellen bis hin zu entscheidenden Verschiebungen in LE
 Die menschlichen Kosten für das Gespräch mit Maschinen: Kann sich ein Chatbot wirklich darum kümmern?Apr 11, 2025 pm 12:00 PM
Die menschlichen Kosten für das Gespräch mit Maschinen: Kann sich ein Chatbot wirklich darum kümmern?Apr 11, 2025 pm 12:00 PMDie beruhigende Illusion der Verbindung: Blühen wir in unseren Beziehungen zur KI wirklich auf? Diese Frage stellte den optimistischen Ton des "Fortschritts -Menschen mit AI) des MIT Media Lab in Frage. Während die Veranstaltung moderne EDG präsentierte
 Verständnis der Scipy Library in PythonApr 11, 2025 am 11:57 AM
Verständnis der Scipy Library in PythonApr 11, 2025 am 11:57 AMEinführung Stellen Sie sich vor, Sie sind ein Wissenschaftler oder Ingenieur, der sich mit komplexen Problemen befasst - Differentialgleichungen, Optimierungsherausforderungen oder Fourier -Analysen. Pythons Benutzerfreundlichkeit und Grafikfunktionen sind ansprechend, aber diese Aufgaben erfordern leistungsstarke Tools
 3 Methoden zum Ausführen von LLAMA 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AM
3 Methoden zum Ausführen von LLAMA 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AMMETAs Lama 3.2: Ein multimodales KI -Kraftpaket Das neueste multimodale Modell von META, Lama 3.2, stellt einen erheblichen Fortschritt in der KI dar, das ein verbessertes Sprachverständnis, eine verbesserte Genauigkeit und die überlegenen Funktionen der Textgenerierung bietet. Seine Fähigkeit t
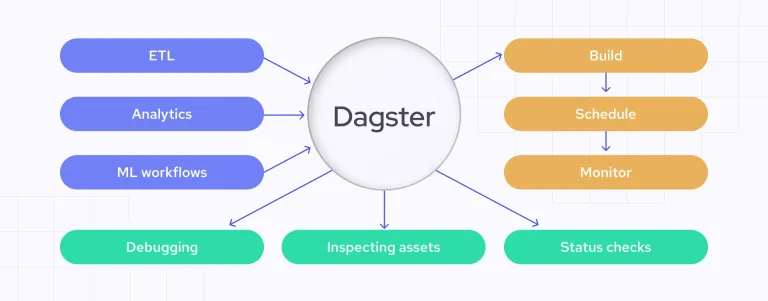 Automatisierung von Datenqualitätsprüfungen mit DagsterApr 11, 2025 am 11:44 AM
Automatisierung von Datenqualitätsprüfungen mit DagsterApr 11, 2025 am 11:44 AMDatenqualitätssicherung: Automatisieren von Schecks mit Dagster und großen Erwartungen Die Aufrechterhaltung einer hohen Datenqualität ist für datengesteuerte Unternehmen von entscheidender Bedeutung. Wenn Datenvolumina und Quellen zunehmen, wird die manuelle Qualitätskontrolle ineffizient und anfällig für Fehler.
 Haben Mainframes eine Rolle in der KI -Ära?Apr 11, 2025 am 11:42 AM
Haben Mainframes eine Rolle in der KI -Ära?Apr 11, 2025 am 11:42 AMMainframes: Die unbesungenen Helden der KI -Revolution Während die Server bei allgemeinen Anwendungen und mehreren Kunden übernommen werden, werden Mainframes für hochvolumige, missionskritische Aufgaben erstellt. Diese leistungsstarken Systeme sind häufig in Heavil gefunden


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

DVWA
Damn Vulnerable Web App (DVWA) ist eine PHP/MySQL-Webanwendung, die sehr anfällig ist. Seine Hauptziele bestehen darin, Sicherheitsexperten dabei zu helfen, ihre Fähigkeiten und Tools in einem rechtlichen Umfeld zu testen, Webentwicklern dabei zu helfen, den Prozess der Sicherung von Webanwendungen besser zu verstehen, und Lehrern/Schülern dabei zu helfen, in einer Unterrichtsumgebung Webanwendungen zu lehren/lernen Sicherheit. Das Ziel von DVWA besteht darin, einige der häufigsten Web-Schwachstellen über eine einfache und unkomplizierte Benutzeroberfläche mit unterschiedlichen Schwierigkeitsgraden zu üben. Bitte beachten Sie, dass diese Software

SAP NetWeaver Server-Adapter für Eclipse
Integrieren Sie Eclipse mit dem SAP NetWeaver-Anwendungsserver.

EditPlus chinesische Crack-Version
Geringe Größe, Syntaxhervorhebung, unterstützt keine Code-Eingabeaufforderungsfunktion

Dreamweaver Mac
Visuelle Webentwicklungstools

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung





