Heim >Backend-Entwicklung >Python-Tutorial >Detaillierte Erläuterung des Bellman-Ford-Algorithmus und der Implementierung in Python
Detaillierte Erläuterung des Bellman-Ford-Algorithmus und der Implementierung in Python
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2024-01-22 19:39:131366Durchsuche
Der Bellman-Ford-Algorithmus kann den kürzesten Weg vom Zielknoten zu anderen Knoten im gewichteten Diagramm finden. Dies ist dem Dijkstra-Algorithmus sehr ähnlich. Der Bellman-Ford-Algorithmus kann Diagramme mit negativen Gewichten verarbeiten und ist hinsichtlich der Implementierung relativ einfach.
Detaillierte Erläuterung des Prinzips des Bellman-Ford-Algorithmus
Der Bellman-Ford-Algorithmus findet iterativ neue Pfade, die kürzer als die überschätzten Pfade sind, indem er die Pfadlängen vom Startscheitelpunkt zu allen anderen Scheitelpunkten überschätzt.
Da wir die Pfadentfernung jedes Knotens aufzeichnen möchten, können wir sie in einem Array der Größe n speichern, wobei n auch die Anzahl der Knoten darstellt.
Instanzdiagramm
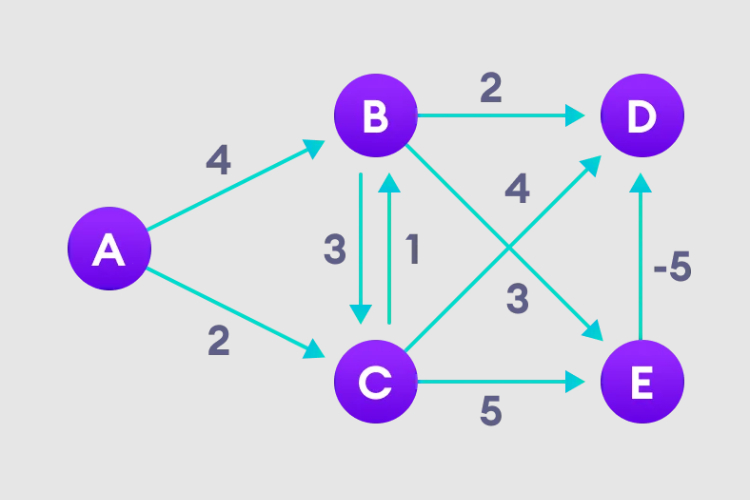
1 Wählen Sie den Startknoten aus, weisen Sie ihn unbegrenzt allen anderen Scheitelpunkten zu und zeichnen Sie den Pfadwert auf.
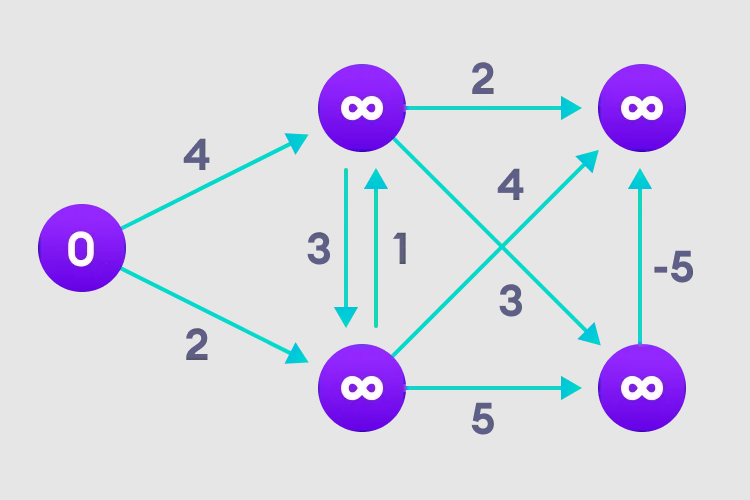
2. Besuchen Sie jede Kante und führen Sie eine Entspannungsoperation durch, um den kürzesten Pfad kontinuierlich zu aktualisieren.
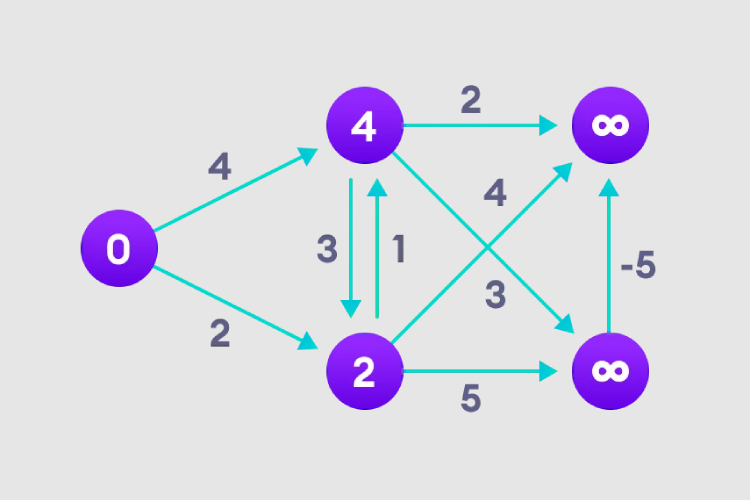
3. Wir müssen dies N-1-mal tun, da im schlimmsten Fall die kürzeste Knotenpfadlänge möglicherweise N-1-mal angepasst werden muss.
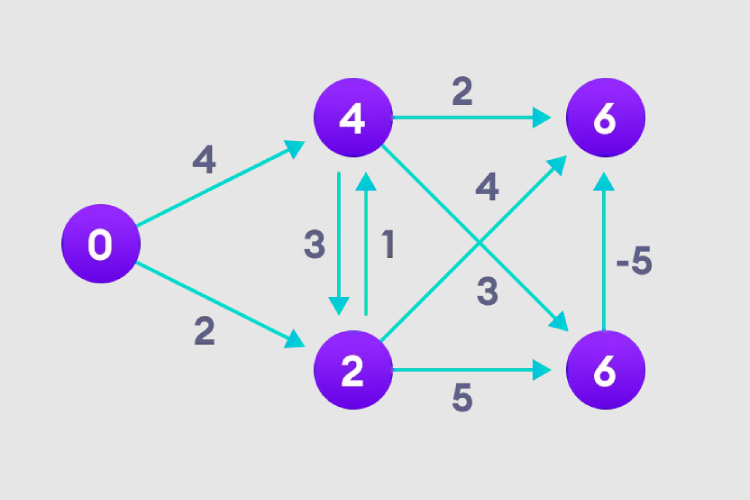
4. Beachten Sie, wie der Knoten in der oberen rechten Ecke seine Pfadlänge anpasst.
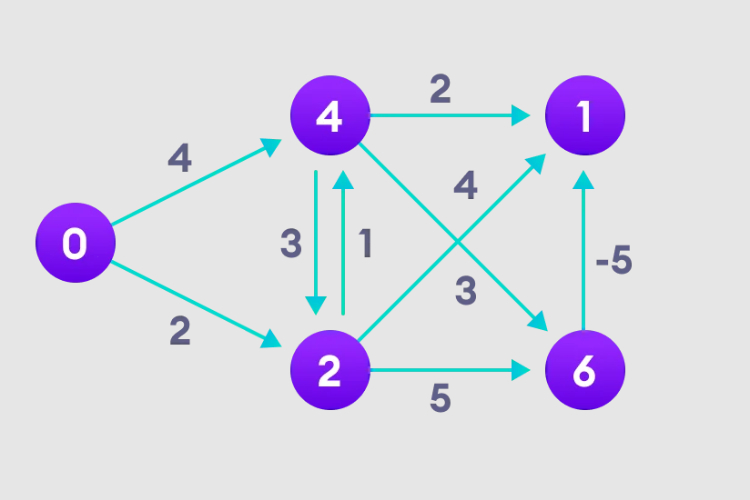
5. Nachdem alle Knoten Pfadlängen haben, prüfen Sie, ob eine negative Schleife vorhanden ist.
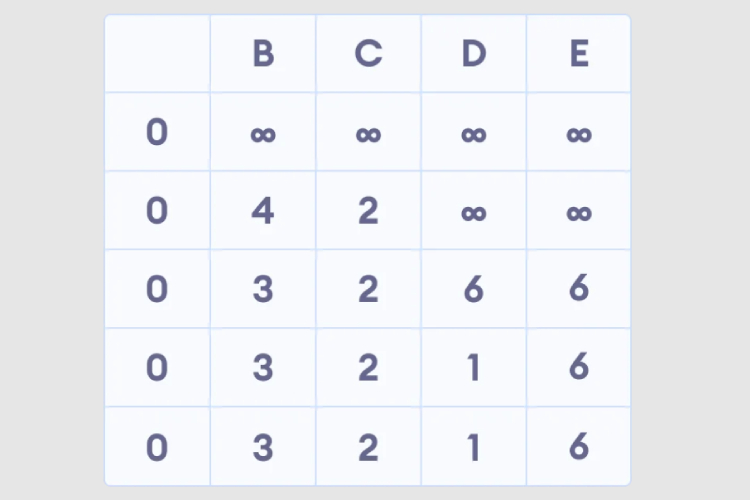
Python implementiert den Bellman-Ford-Algorithmus
class Graph:
def __init__(self, vertices):
self.V = vertices # Total number of vertices in the graph
self.graph = [] # Array of edges
def add_edge(self, s, d, w):
self.graph.append([s, d, w])
def print_solution(self, dist):
print("Vertex Distance from Source")
for i in range(self.V):
print("{0}\t\t{1}".format(i, dist[i]))
def bellman_ford(self, src):
dist = [float("Inf")] * self.V
dist[src] = 0
for _ in range(self.V - 1):
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
dist[d] = dist[s] + w
for s, d, w in self.graph:
if dist[s] != float("Inf") and dist[s] + w < dist[d]:
print("Graph contains negative weight cycle")
return
self.print_solution(dist)
g = Graph(5)
g.add_edge(0, 1, 5)
g.add_edge(0, 2, 4)
g.add_edge(1, 3, 3)
g.add_edge(2, 1, 6)
g.add_edge(3, 2, 2)
g.bellman_ford(0)Das obige ist der detaillierte Inhalt vonDetaillierte Erläuterung des Bellman-Ford-Algorithmus und der Implementierung in Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

