Heim >Computer-Tutorials >Computerwissen >Matlab-Implementierungsmethode und grafische Darstellung numerischer und analytischer Lösungen des Anfangswertproblems von Differentialgleichungen innerhalb eines Intervalls
Matlab-Implementierungsmethode und grafische Darstellung numerischer und analytischer Lösungen des Anfangswertproblems von Differentialgleichungen innerhalb eines Intervalls
- PHPznach vorne
- 2024-01-22 16:54:051237Durchsuche
Verwenden Sie Matlab, um das Anfangswertproblem von Differentialgleichungen zu lösen. Die numerische Lösung und der analytische Lösungsbereich sind Intervalle und werden gezeichnet
Verwenden Sie Matlab, um die Differentialgleichung 5261, die numerische Lösung 4102, das Anfangswertproblem und die analytische Lösung zu lösen. Sie können damit folgendermaßen umgehen:
1. Numerische Lösung
Die numerische Lösung des Anfangswertproblems von Differentialgleichungen kann mit der Ode-Funktion gelöst werden.
Passen Sie zunächst die Funktion der Differentialgleichung an, das heißt
dy = 3/x*y+x^3*(exp(x)+cos(x))-2*x;
Zweitens bestimmen Sie die Anfangsbedingungen
y0=[(exp(pi)+2/pi)*pi^3];
Drittens verwenden Sie die Funktion ode45, um ihre numerische Lösung [x, y] zu finden
2. Analytische Lösung
Die analytische Lösung des Anfangswertproblems von Differentialgleichungen kann mit der dsolve-Funktion gelöst werden.
Deklarieren Sie zunächst eine Variable für y(x), also
syms y(x)
Zweitens die erste Ableitung von y(x), also
Dy=diff(y,1)
Drittens verwenden Sie die dsolve-Funktion, um den Ausdruck ihrer analytischen Lösung y(x) zu finden
y=dsolve(Dy==3/x*y+x^3*(exp(x)+cos(x))-2*x,y(pi)==(exp(pi)+2/pi) *pi^3)
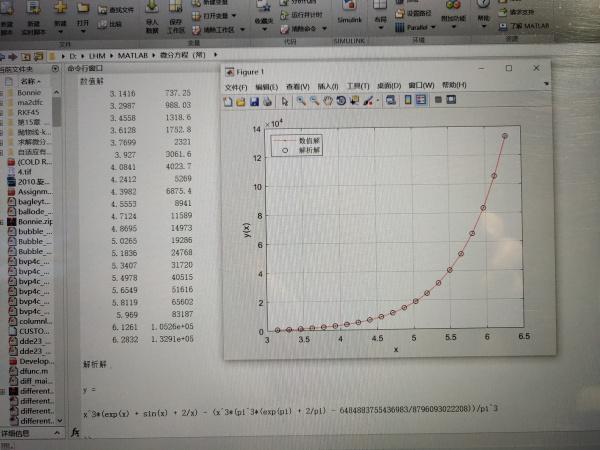
3. Zeichnen Sie numerische Lösungs- und analytische Lösungskurven
Verwenden Sie zunächst die Plot-Funktion, um die Kurve der numerischen Lösung zu zeichnen
plot(x.y)
Zweitens berechnen Sie den y-Wert, der y für eine Reihe von Werten von x im [π, 2π]-Intervall entspricht
Drittens verwenden Sie die Plot-Funktion, um die Kurve der analytischen Lösung zu zeichnen
Nachdem Sie den Code ausgeführt haben, können Sie die folgenden Ergebnisse erhalten.
Matlab-Problem
%%%%%%%%%%%%%%%%%% Quellprogramm
i=0;equ=0;sum=0;
data=input('bitte Nummer eingeben: ');
while(data~=0)
sum=sum+data;
key=input('bitte weitermachen: ');
data=key;
i=i+1;
Ende
equ=sum/i;
equ,sum
%%%%%%%%%%%%%%%%%%%%%%
Ausführungsergebnis:
Bitte geben Sie die Nummer ein: 1
bitte weitermachen: 2
bitte weitermachen: 3
bitte weitermachen: 4
bitte weitermachen: 5
bitte weitermachen: 0
equ =
3
Summe =
15
Das obige ist der detaillierte Inhalt vonMatlab-Implementierungsmethode und grafische Darstellung numerischer und analytischer Lösungen des Anfangswertproblems von Differentialgleichungen innerhalb eines Intervalls. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

