Heim >Backend-Entwicklung >Python-Tutorial >Codelogik zur Implementierung eines Mini-Batch-Gradientenabstiegsalgorithmus mit Python
Codelogik zur Implementierung eines Mini-Batch-Gradientenabstiegsalgorithmus mit Python
- PHPznach vorne
- 2024-01-22 12:33:191627Durchsuche
Lassen Sie Theta = Modellparameter und max_iters = Anzahl der Epochen. Für itr=1,2,3,...,max_iters: Für mini_batch(X_mini,y_mini):
Vorwärtsdurchlauf von Batch X_mini:
1. Prognostizieren Sie den Mini-Batch
2 Parameter Berechnen Sie den Vorhersagefehler (J(Theta))
Nach der Übertragung: Berechnen Sie den Gradienten (Theta)=J(Theta)bzgl. der partiellen Ableitung von Theta
Aktualisierungsparameter: Theta=Theta–Lernrate*Gradient(Theta)
Python implementiert den Codefluss des Gradientenabstiegsalgorithmus
Schritt 1: Importieren Sie Abhängigkeiten, generieren Sie Daten für die lineare Regression und visualisieren Sie die generierten Daten. Nehmen Sie 8000 Datenbeispiele, jedes Beispiel verfügt über 2 Attributfunktionen. Diese Datenproben werden weiter in Trainingssätze (X_train, y_train) und Testsätze (X_test, y_test) mit 7200 bzw. 800 Proben unterteilt.
import numpy as np import matplotlib.pyplot as plt mean=np.array([5.0,6.0]) cov=np.array([[1.0,0.95],[0.95,1.2]]) data=np.random.multivariate_normal(mean,cov,8000) plt.scatter(data[:500,0],data[:500,1],marker='.') plt.show() data=np.hstack((np.ones((data.shape[0],1)),data)) split_factor=0.90 split=int(split_factor*data.shape[0]) X_train=data[:split,:-1] y_train=data[:split,-1].reshape((-1,1)) X_test=data[split:,:-1] y_test=data[split:,-1].reshape((-1,1)) print(& quot Number of examples in training set= % d & quot % (X_train.shape[0])) print(& quot Number of examples in testing set= % d & quot % (X_test.shape[0]))
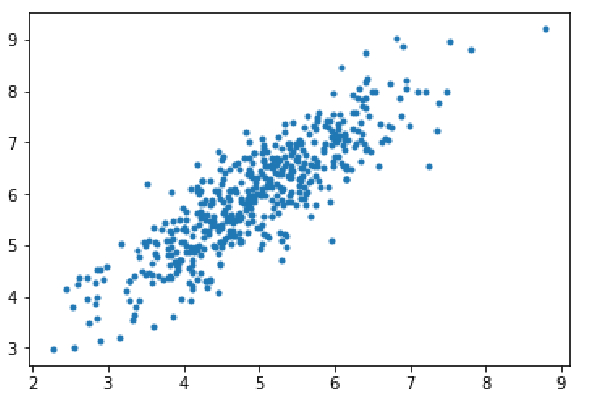
Anzahl der Beispiele im Trainingssatz = 7200 Anzahl der Beispiele im Testsatz = 800
Schritt 2:
Code zur Implementierung der linearen Regression mithilfe eines Mini-Batch-Gradientenabstiegs. gradientDescent() ist die Hauptantriebsfunktion, und andere Funktionen sind Hilfsfunktionen:
Vorhersagen treffen – hypothesis()
Berechnen Sie den Gradienten – gradient()
Berechnen Sie den Fehler – cost()
Erstellen Sie Mini-Batches – create_mini_batches ( )
Die Treiberfunktion initialisiert die Parameter, berechnet den optimalen Parametersatz für das Modell und gibt diese Parameter zusammen mit einer Liste zurück, die den Fehlerverlauf enthält, während die Parameter aktualisiert wurden.
def hypothesis(X,theta):
return np.dot(X,theta)
def gradient(X,y,theta):
h=hypothesis(X,theta)
grad=np.dot(X.transpose(),(h-y))
return grad
def cost(X,y,theta):
h=hypothesis(X,theta)
J=np.dot((h-y).transpose(),(h-y))
J/=2
return J[0]
def create_mini_batches(X,y,batch_size):
mini_batches=[]
data=np.hstack((X,y))
np.random.shuffle(data)
n_minibatches=data.shape[0]//batch_size
i=0
for i in range(n_minibatches+1):
mini_batch=data[i*batch_size:(i+1)*batch_size,:]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
if data.shape[0]%batch_size!=0:
mini_batch=data[i*batch_size:data.shape[0]]
X_mini=mini_batch[:,:-1]
Y_mini=mini_batch[:,-1].reshape((-1,1))
mini_batches.append((X_mini,Y_mini))
return mini_batches
def gradientDescent(X,y,learning_rate=0.001,batch_size=32):
theta=np.zeros((X.shape[1],1))
error_list=[]
max_iters=3
for itr in range(max_iters):
mini_batches=create_mini_batches(X,y,batch_size)
for mini_batch in mini_batches:
X_mini,y_mini=mini_batch
theta=theta-learning_rate*gradient(X_mini,y_mini,theta)
error_list.append(cost(X_mini,y_mini,theta))
return theta,error_listRufen Sie die Funktion „gradientDescent()“ auf, um die Modellparameter (Theta) zu berechnen und die Änderungen in der Fehlerfunktion zu visualisieren.
theta,error_list=gradientDescent(X_train,y_train)
print("Bias=",theta[0])
print("Coefficients=",theta[1:])
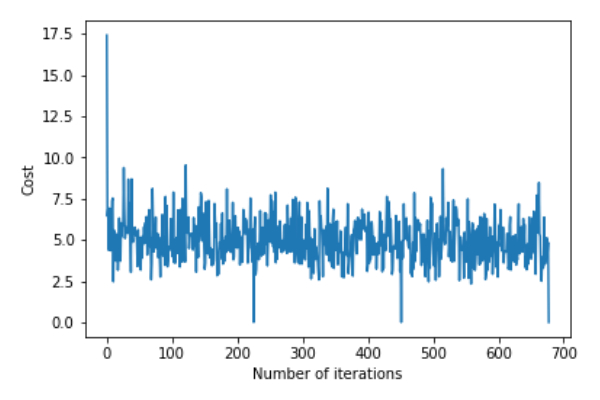
plt.plot(error_list)
plt.xlabel("Number of iterations")
plt.ylabel("Cost")
plt.show()Abweichung=[0,81830471]Koeffizient=[[1,04586595]]
Schritt 3: Testsatz vorhersagen und den mittleren absoluten Fehler in der Vorhersage berechnen.
y_pred=hypothesis(X_test,theta) plt.scatter(X_test[:,1],y_test[:,],marker='.') plt.plot(X_test[:,1],y_pred,color='orange') plt.show() error=np.sum(np.abs(y_test-y_pred)/y_test.shape[0]) print(& quot Mean absolute error=",error)
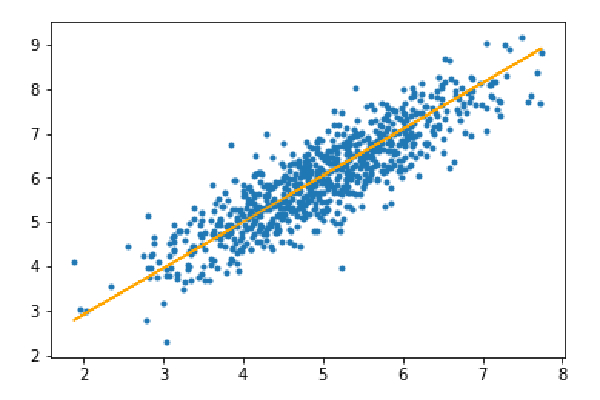
Mittlerer absoluter Fehler = 0,4366644295854125
Die orangefarbene Linie stellt die endgültige Hypothesenfunktion dar: Theta[0]+Theta[1]*X_test[:,1]+Theta[2]*X_test[:,2]=0
Das obige ist der detaillierte Inhalt vonCodelogik zur Implementierung eines Mini-Batch-Gradientenabstiegsalgorithmus mit Python. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

