 Technologie-Peripheriegeräte
Technologie-Peripheriegeräte KI
KI Die University of Science and Technology of China entwickelt die Methode „State Sequence Frequency Domain Prediction', die die Leistung um 20 % verbessert und die Probeneffizienz maximiert.
Die University of Science and Technology of China entwickelt die Methode „State Sequence Frequency Domain Prediction', die die Leistung um 20 % verbessert und die Probeneffizienz maximiert.Der Trainingsprozess des Verstärkungslernalgorithmus (Reinforcement Learning, RL) erfordert normalerweise eine große Menge an Beispieldaten, die mit der Umgebung interagieren, um sie zu unterstützen. In der realen Welt ist es jedoch oft sehr kostspielig, eine große Anzahl von Interaktionsproben zu sammeln, oder die Sicherheit des Probenahmeprozesses kann nicht gewährleistet werden, wie beispielsweise beim UAV-Luftkampftraining und beim autonomen Fahrtraining. Dieses Problem schränkt den Umfang des verstärkenden Lernens in vielen praktischen Anwendungen ein. Daher haben Forscher intensiv daran gearbeitet, herauszufinden, wie ein Gleichgewicht zwischen Probeneffizienz und Sicherheit gefunden werden kann, um dieses Problem zu lösen. Eine mögliche Lösung besteht darin, Simulatoren oder virtuelle Umgebungen zu nutzen, um große Mengen an Beispieldaten zu generieren und so die Kosten und Sicherheitsrisiken realer Situationen zu vermeiden. Um die Stichprobeneffizienz von Reinforcement-Learning-Algorithmen während des Trainingsprozesses zu verbessern, haben einige Forscher außerdem Repräsentationslerntechnologien verwendet, um Hilfsaufgaben zur Vorhersage zukünftiger Zustandssignale zu entwerfen. Auf diese Weise können Algorithmen aus dem ursprünglichen Umweltzustand Merkmale extrahieren und kodieren, die für zukünftige Entscheidungen relevant sind. Der Zweck dieses Ansatzes besteht darin, die Leistung von Reinforcement-Learning-Algorithmen zu verbessern, indem mehr Informationen über die Umgebung gelernt und eine bessere Grundlage für die Entscheidungsfindung bereitgestellt werden. Auf diese Weise kann der Algorithmus Beispieldaten während des Trainingsprozesses effizienter nutzen, den Lernprozess beschleunigen und die Genauigkeit und Effizienz der Entscheidungsfindung verbessern.
Basierend auf dieser Idee wurde in dieser Arbeit eine Hilfsaufgabe entworfen, um die Zustandssequenz-Häufigkeitsbereichsverteilung
für mehrere Schritte in der Zukunft vorherzusagen, um längerfristige zukünftige Entscheidungsmerkmale zu erfassen und dadurch die Stichprobeneffizienz des Algorithmus zu verbessern .Diese Arbeit trägt den Titel State Sequences Prediction via Fourier Transform for Representation Learning, wurde in NeurIPS 2023 veröffentlicht und als Spotlight akzeptiert.
Autorenliste: Ye Mingxuan, Kuang Yufei, Wang Jie*, Yang Rui, Zhou Wengang, Li Houqiang, Wu Feng
Link zum Papier: https://openreview.net/forum?id= MvoMDD6emT
Code-Link: https://github.com/MIRALab-USTC/RL-SPF/
Forschungshintergrund und Motivation
Deep Reinforcement Learning-Algorithmus in der Robotersteuerung [1], Spielintelligenz [ 2], Große Erfolge wurden in Bereichen wie der kombinatorischen Optimierung [3] erzielt. Allerdings leidet der aktuelle Reinforcement-Learning-Algorithmus immer noch unter dem Problem der „geringen Stichprobeneffizienz“, d. h. der Roboter benötigt eine große Datenmenge, die mit der Umgebung interagiert, um eine Strategie mit hervorragender Leistung zu trainieren.
Um die Stichprobeneffizienz zu verbessern, haben Forscher begonnen, sich auf das Lernen von Darstellungen zu konzentrieren, in der Hoffnung, dass die durch Training erhaltenen Darstellungen umfangreiche und nützliche Merkmalsinformationen aus dem ursprünglichen Zustand der Umgebung extrahieren und so die Erkundungseffizienz des Roboters in der Umgebung verbessern können Zustandsraum.
Reinforcement-Learning-Algorithmus-Framework basierend auf Repräsentationslernen

„Langzeitsequenzsignale“im Vergleich mehr zukünftige Informationen, die für die langfristige Entscheidungsfindung von Vorteil sind zu Einzelschrittsignalen. Inspiriert von dieser Sichtweise haben einige Forscher vorgeschlagen, das Repräsentationslernen durch die Vorhersage mehrstufiger Zustandssequenzsignale in der Zukunft zu unterstützen [4,5]. Es ist jedoch sehr schwierig, die Zustandssequenz direkt vorherzusagen, um das Repräsentationslernen zu unterstützen.
Unter den beiden vorhandenen Methoden generiert eine Methode schrittweise den zukünftigen Zustand in einem einzigen Moment, indem sie das „einstufige Wahrscheinlichkeitsübergangsmodell“ lernt, um die mehrstufige Zustandssequenz indirekt vorherzusagen [6,7]. Diese Art von Methode erfordert jedoch eine hohe Genauigkeit des trainierten Wahrscheinlichkeitsübertragungsmodells, da sich der Vorhersagefehler bei jedem Schritt mit zunehmender Länge der Vorhersagesequenz ansammelt.
Eine andere Art von Methode unterstützt das Repräsentationslernen [8] durchdirekte Vorhersage der Zustandssequenz mehrerer Schritte in der Zukunft[8], aber diese Art von Methode muss die mehrstufige reale Zustandssequenz als Bezeichnung speichern der Vorhersageaufgabe, die viel Speicherplatz verbraucht. Daher ist es ein Problem, das gelöst werden muss, wie aus der Zustandssequenz der Umgebung zukünftige Informationen, die für die langfristige Entscheidungsfindung von Vorteil sind, effektiv extrahiert und dadurch die Probeneffizienz während des kontinuierlichen Kontrollrobotertrainings verbessert werden kann.
Um die oben genannten Probleme zu lösen, schlagen wir eine Repräsentationslernmethode vor, die auf der Vorhersage der Zustandssequenzfrequenzdomäne basiert (State Sequences Prediction via F
ourier Transform,SPF). „Frequenzbereichsverteilung der Zustandssequenz“ zu verwenden, um Trend- und Regelmäßigkeitsinformationen in Zustandssequenzdaten explizit zu extrahieren und so die Darstellung bei der effizienten Extraktion langfristiger zukünftiger Informationen zu unterstützen. Wir haben theoretisch bewiesen, dass es „zwei Arten von Strukturinformationen“ in der Zustandssequenz gibt, zum einen Trendinformationen im Zusammenhang mit der Strategieleistung und zum anderen Regelmäßigkeitsinformationen im Zusammenhang mit der Statusperiodizität. Bevor wir die beiden Strukturinformationen im Detail analysieren, stellen wir zunächst die relevanten Definitionen von Markov-Entscheidungsprozessen (MDP) vor, die Zustandssequenzen erzeugen. Wir betrachten den klassischen Markov-Entscheidungsprozess in einem kontinuierlichen Kontrollproblem, das durch ein Fünffach dargestellt werden kann. Darunter sind der entsprechende Zustand und Aktionsraum, die Belohnungsfunktion, die Zustandsübergangsfunktion der Umgebung, die Anfangsverteilung des Zustands und der Abzinsungsfaktor. Darüber hinaus verwenden wir zur Darstellung der Aktionsverteilung der Politik im Bundesstaat. Wir zeichnen den aktuellen Status des Agenten als auf und die ausgewählte Aktion als Nachdem der Agent die Aktion ausgeführt hat, wechselt die Umgebung im nächsten Moment in den Status und gibt Belohnungen an den Agenten zurück. Wir zeichnen die Trajektorie auf, die dem Zustand und der Aktion entspricht, die während der Interaktion zwischen dem Agenten und der Umgebung erhalten wird, und die Trajektorie folgt der Verteilung. Das Ziel des Reinforcement-Learning-Algorithmus besteht darin, die erwartete kumulative Rendite in der Zukunft zu maximieren. Wir verwenden, um die durchschnittliche kumulative Rendite unter dem aktuellen Strategie- und Umgebungsmodell darzustellen, und abgekürzt als , was wie folgt definiert ist: zeigt die Leistung der aktuellen Strategie. Im Folgenden stellen wir das „erste Strukturmerkmal“ der Zustandssequenz vor, das die Abhängigkeit zwischen der Zustandssequenz und der entsprechenden Belohnungssequenz beinhaltet und die Leistung der aktuellen Strategie zeigen kann. Trend . Bei Verstärkungslernaufgaben bestimmt die zukünftige Zustandssequenz weitgehend die Reihenfolge der Aktionen, die der Agent in der Zukunft durchführt, und bestimmt darüber hinaus die entsprechende Belohnungssequenz. Daher enthält die zukünftige Zustandssequenz nicht nur Informationen über die der Umgebung inhärente Wahrscheinlichkeitsübergangsfunktion, sondern kann auch dabei helfen, den Trend der aktuellen Strategie zu erfassen. Inspiriert von der obigen Struktur haben wir den folgenden Satz bewiesen, um die Existenz dieser strukturellen Abhängigkeit weiter zu demonstrieren: Satz 1: Wenn die Belohnungsfunktion nur mit dem Zustand zusammenhängt, dann für zwei beliebige Strategien und ihre Leistungsunterschiede können durch den Unterschied in den durch diese beiden Strategien erzeugten Zustandssequenzverteilungen gesteuert werden: Stellt in der obigen Formel die Wahrscheinlichkeitsverteilung der Zustandssequenz unter den Bedingungen der angegebenen Strategie und Übergangswahrscheinlichkeitsfunktion dar, und stellt die Norm dar. Der obige Satz zeigt, dass der Verteilungsunterschied zwischen den beiden entsprechenden Zustandssequenzen umso größer ist, je größer der Leistungsunterschied zwischen den beiden Strategien ist. Dies bedeutet, dass eine gute und eine schlechte Strategie zwei völlig unterschiedliche Zustandssequenzen erzeugen, was weiter verdeutlicht, dass die in der Zustandssequenz enthaltenen langfristigen Strukturinformationen möglicherweise die Effizienz der Suchstrategie bei hervorragender Leistung beeinflussen können. Andererseits kann die Frequenzbereichsverteilungsdifferenz der Zustandssequenz unter bestimmten Bedingungen auch eine Obergrenze für die entsprechende Richtlinienleistungsdifferenz liefern, wie im folgenden Satz gezeigt: Satz 2 : Wenn der Zustand Der Raum ist endlichdimensional und die Belohnungsfunktion ist ein Polynom n-Grades, das sich auf den Zustand bezieht, dann kann der Leistungsunterschied zwischen zwei beliebigen Strategien und durch den Unterschied in der Frequenzbereichsverteilung der erzeugten Zustandssequenzen gesteuert werden durch diese beiden Strategien: Stellt in der obigen Formel die Fourier-Funktion der Potenzfolge der durch die Richtlinie erzeugten Zustandsfolge dar und stellt die te Komponente der Fourier-Funktion dar. Dieses Theorem zeigt, dass die Frequenzbereichsverteilung der Zustandssequenz immer noch Merkmale enthält, die für die aktuelle Richtlinienleistung relevant sind. Regelmäßige Informationen vor, das in der Zustandssequenz existiert und die Zeitabhängigkeit zwischen Zustandssignalen beinhaltet, also die Zustandssequenz über einen langen Zeitraum normales Muster ausgestellt. Bei vielen realen Aufgaben zeigen Agenten auch periodisches Verhalten, da die Zustandsübergangsfunktion ihrer Umgebung selbst periodisch ist. Nehmen Sie als Beispiel einen industriellen Montageroboter. Der Roboter wird darauf trainiert, Teile zusammenzubauen, um ein Endprodukt zu erstellen. Wenn das Strategietraining Stabilität erreicht, führt er eine periodische Aktionssequenz aus, die es ihm ermöglicht, Teile effizient zusammenzubauen. Inspiriert durch das obige Beispiel liefern wir einige theoretische Analysen, um zu beweisen, dass im endlichen Zustandsraum, wenn die Übergangswahrscheinlichkeitsmatrix bestimmte Annahmen erfüllt, die entsprechende Zustandssequenz „allmählich“ angezeigt werden kann, wenn der Agent eine stabile Strategie erreicht . „Fast periodisch“, der spezifische Satz lautet wie folgt: Satz 3: Für einen endlichdimensionalen Zustandsraum mit einer Zustandsübergangsmatrix, vorausgesetzt, es gibt zyklische Klassen, die entsprechende Zustandsübergangsuntermatrix ist. Angenommen, die Anzahl der Eigenwerte dieser Matrix mit Modul 1 beträgt, dann zeigt die Zustandsverteilung für die Anfangsverteilung eines beliebigen Zustands eine asymptotische Periodizität mit der Periode. Wenn in der MuJoCo-Aufgabe das Richtlinientraining Stabilität erreicht, zeigt der Agent auch periodische Bewegungen. Die folgende Abbildung zeigt ein Beispiel für die Zustandssequenz des HalfCheetah-Agenten in der MuJoCo-Aufgabe über einen bestimmten Zeitraum, wobei eine offensichtliche Periodizität beobachtet werden kann. (Weitere Beispiele für periodische Zustandssequenzen in der MuJoCo-Aufgabe finden Sie in Abschnitt E im Anhang dieses Dokuments.) Die Periodizität des Zustands des HalfCheetah-Agenten in der MuJoCo-Aufgabe über einen bestimmten Zeitraum Die durch Zeitreihen im Zeitbereich dargestellten Informationen sind relativ verstreut, im Frequenzbereich werden die regulären Informationen in der Sequenz jedoch in konzentrierterer Form dargestellt. Durch die Analyse der Frequenzkomponenten im Frequenzbereich können wir die in der Zustandssequenz vorhandenen periodischen Eigenschaften explizit erfassen. Im vorherigen Teil haben wir theoretisch bewiesen, dass die Frequenzbereichsverteilung der Zustandssequenz die Leistung der Strategie widerspiegeln kann, und durch die Analyse der Frequenzkomponenten im Frequenzbereich können wir dies explizit Erfassen Sie die periodischen Merkmale der Zustandssequenz. Inspiriert von der obigen Analyse haben wir die Hilfsaufgabe „Vorhersage der Fourier-Transformation einer unendlichstufigen zukünftigen Zustandsfolge“ entworfen, um die Darstellung zum Extrahieren von Strukturinformationen in der Zustandsfolge zu ermutigen. Im Folgenden wird unsere Modellierung dieser Hilfsaufgabe vorgestellt. Angesichts des aktuellen Zustands und der aktuellen Aktion definieren wir die zukünftige Zustandssequenzerwartung wie folgt: Unsere Hilfsaufgabe trainiert eine Darstellung, um die diskrete Zeit-Fourier-Transformation (DTFT) der obigen Zustandssequenzerwartung vorherzusagen ist, Die obige Fourier-Transformationsformel kann in die folgende rekursive Form umgeschrieben werden: wo, wo , Dimensionen des Zustandsraums, ist die Anzahl der Diskretisierungspunkte der Fourier-Funktion der vorhergesagten Zustandsfolge. Inspiriert von der TD-Fehler-Verlustfunktion [9], die Q-Wert-Netzwerke im Q-Learning optimiert, haben wir die folgende Verlustfunktion entworfen: Dazu gehören die neuronalen Netzwerkparameter des Repräsentationsencoders (Encoder) und des Fourier-Funktionsprädiktors (Prädiktor), für die die Verlustfunktion optimiert werden muss, und der Erfahrungspool zum Speichern von Beispieldaten. Darüber hinaus können wir beweisen, dass die obige rekursive Formel als Komprimierungskarte ausgedrückt werden kann: Theorem 4: Stellen Sie die Funktionsfamilie dar und definieren Sie die Norm auf wobei stellt den Zeilenvektor der Matrix dar. Wir definieren die Zuordnung als und es kann bewiesen werden, dass es sich um eine Kompressionszuordnung handelt. Gemäß dem Komprimierungszuordnungsprinzip können wir den Operator iterativ verwenden, um die Frequenzbereichsverteilung der realen Zustandssequenz anzunähern, und haben eine Konvergenzgarantie in der tabellarischen Einstellung. Darüber hinaus hängt die von uns entworfene Verlustfunktion nur vom Zustand des aktuellen Moments und des nächsten Moments ab, sodass die Zustandsdaten mehrerer Schritte in der Zukunft nicht als Vorhersageetiketten gespeichert werden müssen, was Vorteile hat von „einfache Implementierung und geringes Speichervolumen“ . Im Folgenden stellen wir das Algorithmus-Framework der Methode (SPF) in diesem Artikel vor. Wir geben die Zustandsaktionsdaten des aktuellen Moments und des nächsten Moments online (online) und im Ziel ein ( Ziel) bzw. ) Im Darstellungsencoder (Encoder) werden die Zustandsaktionsdarstellungsdaten erhalten und dann werden die Darstellungsdaten in den Fourier-Funktionsprädiktor (Prädiktor) eingegeben, um zum aktuellen Zeitpunkt zwei Sätze von Zustandssequenz-Fourier-Funktionsvorhersagen zu erhalten und im nächsten Moment. Durch Ersetzen dieser beiden Sätze von Fourier-Funktionsvorhersagen können wir den Verlustfunktionswert berechnen. Wir optimieren und aktualisieren den Repräsentationsencoder und den Fourier-Funktionsprädiktor, indem wir die Verlustfunktion minimieren, sodass die Ausgabe des Prädiktors die Fourier-Transformation der realen Zustandssequenz annähern kann, wodurch der Repräsentationsencoder dazu angeregt wird, Merkmale zu extrahieren, die das enthalten langfristige zukünftige Eigenschaften der Strukturinformationen von Zustandssequenzen. Wir geben den ursprünglichen Zustand und die ursprüngliche Aktion in den Repräsentationsencoder ein, verwenden die erhaltenen Merkmale als Eingabe des Akteurnetzwerks und Kritikernetzwerks im Verstärkungslernalgorithmus und verwenden den klassischen Verstärkungslernalgorithmus, um das Akteursnetzwerk und den Kritiker zu optimieren Netzwerk. Experimentelle Ergebnisse (Hinweis: In diesem Abschnitt wird nur ein Teil der experimentellen Ergebnisse ausgewählt. Ausführlichere Ergebnisse finden Sie in Abschnitt 6 und im Anhang des Originalpapiers.) Wir werden die SPF-Methode in der MuJoCo-Simulationsrobotersteuerungsumgebung testen und die folgenden sechs Methoden vergleichen: Die obige Abbildung zeigt die Leistungskurven unserer vorgeschlagenen SPF-Methode (rote Linie und orange Linie) und anderer Vergleichsmethoden in 6 MuJoCo-Aufgaben. Die Ergebnisse zeigen, dass unsere vorgeschlagene Methode im Vergleich zu anderen Methoden eine Leistungsverbesserung von 19,5 % erreichen kann. Wir führten Ablationsexperimente für jedes Modul der SPF-Methode durch und verglichen diese Methode mit der Nichtverwendung des Projektormoduls (noproj), der Nichtverwendung des Zielnetzwerkmoduls (notarg) und der Änderung des Vorhersageverlusts (nofreqloss) Vergleichen Sie die Leistung beim Ändern der Feature-Encoder-Netzwerkstruktur (mlp, mlp_cat). Ablationsexperiment-Ergebnisdiagramm der SPF-Methode, angewendet auf den SAC-Algorithmus, getestet mit der HalfCheetah-Aufgabe Wir verwenden die SPF-Methodetrainierter Prädiktor, um das Fu von auszugeben Die Zustandssequenz-Fourier-Funktion und die durch die Inverse Fourier-Transformation wiederhergestellte 200-Schritte-Zustandssequenz werden mit der echten 200-Schritte-Zustandssequenz verglichen. Die Ergebnisse zeigen, dass die wiederhergestellte Zustandssequenz der realen Zustandssequenz sehr ähnlich ist, selbst wenn ein längerer Zustand als Eingabe verwendet wird. Dies zeigt, dass die durch die SPF-Methode erlernte Darstellung die im Zustand enthaltene Struktur effektiv kodieren kann Reihenfolge. Strukturelle Informationsanalyse in der Zustandssequenz
Markov-Entscheidungsprozess
Trendinformationen

Jetzt stellen wir das
"zweite Strukturmerkmal"
Einführung in die Methode
SPF-Methodenverlustfunktion








Algorithmus-Framework der SPF-Methode
 Algorithmusrahmendiagramm der Repräsentationslernmethode (SPF) basierend auf der Vorhersage der Zustandssequenzfrequenzdomäne
Algorithmusrahmendiagramm der Repräsentationslernmethode (SPF) basierend auf der Vorhersage der Zustandssequenzfrequenzdomäne
Vergleich der Algorithmusleistung
Ablationsexperiment

Visualisierungsexperiment
 Schematisches Diagramm der wiederhergestellten Zustandssequenz basierend auf dem vorhergesagten Wert der Fourier-Funktion, getestet mit der Walker2d-Aufgabe. Darunter ist die blaue Linie ein schematisches Diagramm der realen Zustandssequenz und die fünf roten Linien sind ein schematisches Diagramm der wiederhergestellten Zustandssequenz. Die unteren und helleren roten Linien stellen die unter Verwendung des längeren historischen Zustands wiederhergestellte Zustandssequenz dar.
Schematisches Diagramm der wiederhergestellten Zustandssequenz basierend auf dem vorhergesagten Wert der Fourier-Funktion, getestet mit der Walker2d-Aufgabe. Darunter ist die blaue Linie ein schematisches Diagramm der realen Zustandssequenz und die fünf roten Linien sind ein schematisches Diagramm der wiederhergestellten Zustandssequenz. Die unteren und helleren roten Linien stellen die unter Verwendung des längeren historischen Zustands wiederhergestellte Zustandssequenz dar.
Das obige ist der detaillierte Inhalt vonDie University of Science and Technology of China entwickelt die Methode „State Sequence Frequency Domain Prediction', die die Leistung um 20 % verbessert und die Probeneffizienz maximiert.. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
 Lesen des AI-Index 2025: Ist AI Ihr Freund, Feind oder Co-Pilot?Apr 11, 2025 pm 12:13 PM
Lesen des AI-Index 2025: Ist AI Ihr Freund, Feind oder Co-Pilot?Apr 11, 2025 pm 12:13 PMDer Bericht des Stanford University Institute for Human-orientierte künstliche Intelligenz bietet einen guten Überblick über die laufende Revolution der künstlichen Intelligenz. Interpretieren wir es in vier einfachen Konzepten: Erkenntnis (verstehen, was geschieht), Wertschätzung (Sehenswürdigkeiten), Akzeptanz (Gesichtsherausforderungen) und Verantwortung (finden Sie unsere Verantwortlichkeiten). Kognition: Künstliche Intelligenz ist überall und entwickelt sich schnell Wir müssen uns sehr bewusst sein, wie schnell künstliche Intelligenz entwickelt und ausbreitet. Künstliche Intelligenzsysteme verbessern sich ständig und erzielen hervorragende Ergebnisse bei mathematischen und komplexen Denktests, und erst vor einem Jahr haben sie in diesen Tests kläglich gescheitert. Stellen Sie sich vor, KI zu lösen komplexe Codierungsprobleme oder wissenschaftliche Probleme auf Graduiertenebene-seit 2023-
 Erste Schritte mit Meta Lama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PM
Erste Schritte mit Meta Lama 3.2 - Analytics VidhyaApr 11, 2025 pm 12:04 PMMetas Lama 3.2: Ein Sprung nach vorne in der multimodalen und mobilen KI Meta hat kürzlich Lama 3.2 vorgestellt, ein bedeutender Fortschritt in der KI mit leistungsstarken Sichtfunktionen und leichten Textmodellen, die für mobile Geräte optimiert sind. Aufbau auf dem Erfolg o
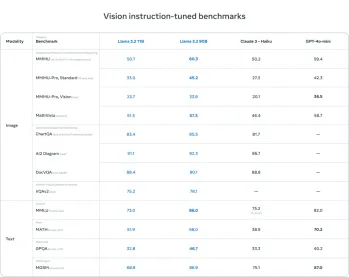 AV -Bytes: META ' S Lama 3.2, Googles Gemini 1.5 und mehrApr 11, 2025 pm 12:01 PM
AV -Bytes: META ' S Lama 3.2, Googles Gemini 1.5 und mehrApr 11, 2025 pm 12:01 PMDie KI -Landschaft dieser Woche: Ein Wirbelsturm von Fortschritten, ethischen Überlegungen und regulatorischen Debatten. Hauptakteure wie OpenAI, Google, Meta und Microsoft haben einen Strom von Updates veröffentlicht, von bahnbrechenden neuen Modellen bis hin zu entscheidenden Verschiebungen in LE
 Die menschlichen Kosten für das Gespräch mit Maschinen: Kann sich ein Chatbot wirklich darum kümmern?Apr 11, 2025 pm 12:00 PM
Die menschlichen Kosten für das Gespräch mit Maschinen: Kann sich ein Chatbot wirklich darum kümmern?Apr 11, 2025 pm 12:00 PMDie beruhigende Illusion der Verbindung: Blühen wir in unseren Beziehungen zur KI wirklich auf? Diese Frage stellte den optimistischen Ton des "Fortschritts -Menschen mit AI) des MIT Media Lab in Frage. Während die Veranstaltung moderne EDG präsentierte
 Verständnis der Scipy Library in PythonApr 11, 2025 am 11:57 AM
Verständnis der Scipy Library in PythonApr 11, 2025 am 11:57 AMEinführung Stellen Sie sich vor, Sie sind ein Wissenschaftler oder Ingenieur, der sich mit komplexen Problemen befasst - Differentialgleichungen, Optimierungsherausforderungen oder Fourier -Analysen. Pythons Benutzerfreundlichkeit und Grafikfunktionen sind ansprechend, aber diese Aufgaben erfordern leistungsstarke Tools
 3 Methoden zum Ausführen von LLAMA 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AM
3 Methoden zum Ausführen von LLAMA 3.2 - Analytics VidhyaApr 11, 2025 am 11:56 AMMETAs Lama 3.2: Ein multimodales KI -Kraftpaket Das neueste multimodale Modell von META, Lama 3.2, stellt einen erheblichen Fortschritt in der KI dar, das ein verbessertes Sprachverständnis, eine verbesserte Genauigkeit und die überlegenen Funktionen der Textgenerierung bietet. Seine Fähigkeit t
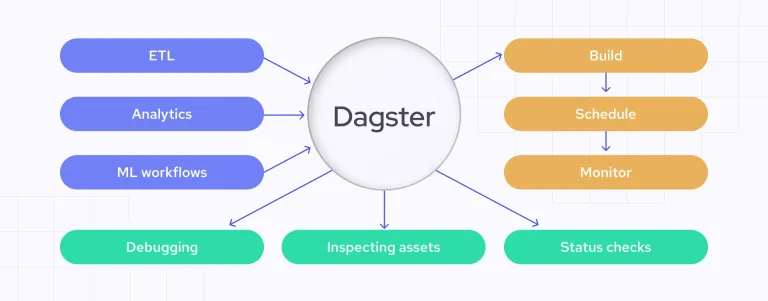 Automatisierung von Datenqualitätsprüfungen mit DagsterApr 11, 2025 am 11:44 AM
Automatisierung von Datenqualitätsprüfungen mit DagsterApr 11, 2025 am 11:44 AMDatenqualitätssicherung: Automatisieren von Schecks mit Dagster und großen Erwartungen Die Aufrechterhaltung einer hohen Datenqualität ist für datengesteuerte Unternehmen von entscheidender Bedeutung. Wenn Datenvolumina und Quellen zunehmen, wird die manuelle Qualitätskontrolle ineffizient und anfällig für Fehler.
 Haben Mainframes eine Rolle in der KI -Ära?Apr 11, 2025 am 11:42 AM
Haben Mainframes eine Rolle in der KI -Ära?Apr 11, 2025 am 11:42 AMMainframes: Die unbesungenen Helden der KI -Revolution Während die Server bei allgemeinen Anwendungen und mehreren Kunden übernommen werden, werden Mainframes für hochvolumige, missionskritische Aufgaben erstellt. Diese leistungsstarken Systeme sind häufig in Heavil gefunden


Heiße KI -Werkzeuge

Undresser.AI Undress
KI-gestützte App zum Erstellen realistischer Aktfotos

AI Clothes Remover
Online-KI-Tool zum Entfernen von Kleidung aus Fotos.

Undress AI Tool
Ausziehbilder kostenlos

Clothoff.io
KI-Kleiderentferner

AI Hentai Generator
Erstellen Sie kostenlos Ai Hentai.

Heißer Artikel

Heiße Werkzeuge

Senden Sie Studio 13.0.1
Leistungsstarke integrierte PHP-Entwicklungsumgebung

Herunterladen der Mac-Version des Atom-Editors
Der beliebteste Open-Source-Editor

Dreamweaver CS6
Visuelle Webentwicklungstools

ZendStudio 13.5.1 Mac
Leistungsstarke integrierte PHP-Entwicklungsumgebung

EditPlus chinesische Crack-Version
Geringe Größe, Syntaxhervorhebung, unterstützt keine Code-Eingabeaufforderungsfunktion





