Berechnen Sie den Schnittpunkt des Quadrats der Kurve y=x und der Geraden x=1 in Java mithilfe der Rekursion

Verwenden Sie die rekursive Methode in Java, um das Quadrat der Kurve y x und die gekrümmte Kante zu berechnen, die von der geraden Linie x 1 x-Achse umgeben ist

öffentliche Klasse Util {

public static void main(String[] args) {

System.out.println(getMj(2000));

}

public static double berechneArea(double n){

if(n==1){

return 1.0;

}sonst{

double r = (n-1) * (n-1) * (n+1) * (2*n+1) / (n * n * n * (2*n-1));

return r*getMj(n-1);

}

}

}

Die Voraussetzung für den rekursiven Algorithmus besteht darin, seine allgemeine Formel zu verstehen. 2000 bedeutet die Aufteilung des gekrümmten Dreiecks in 2000 Rechtecke. Das spezifische Prinzip ist in der folgenden Abbildung zu sehen:

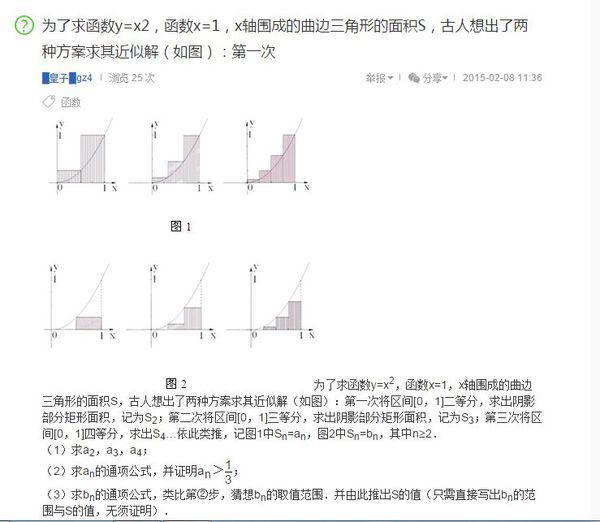
Verwendung des Algorithmus aus Abbildung 1:

an=(n+1)(2n+1) /6n^2

Der einfache Weg, es zu schreiben, ist wie folgt:

öffentliche Klasse Util {

public static void main(String[] args) {

System.out.println(getMj(100000));

}

public static double berechneArea(double n){

return (n+1)*(2*n+1)/(6*n*n);

}

}

Java-Rekursionsproblem

(1) Rekursion ruft sich selbst in einer Prozedur oder Funktion auf

(2) Wenn Sie eine rekursive Strategie verwenden, müssen Sie sicherstellen, dass eine klare Endbedingung für die Rekursion vorliegt, die auch als rekursiver Exit bezeichnet wird.

Rekursive Algorithmen werden im Allgemeinen verwendet, um drei Arten von Problemen zu lösen:

(1) Die Definition von Daten ist rekursiv definiert. (Fibonacci-Funktion)

(2) Die Problemlösung wird nach dem rekursiven Algorithmus implementiert. (Traceback)

(3) Die Strukturform von Daten wird rekursiv definiert.

Das folgende Beispiel berechnet die Fakultät von n rekursiv.

öffentlicher Klassentest {

öffentliches statisches int faktorielles(int n) {

if(n == 0){

return 1;

}sonst{

return n * Faculty(n-1);

}

}

public static void main(String[] args) {

System.out.println(factorial(3));

}

}

Der rekursive Algorithmus zur Halbierung der Suche in der Java-Datenstruktur erfordert fachmännische Anleitung!

Paketquelle;

öffentliche Klassensuche {

öffentliche statische boolesche Binärsuche(int[] a, int x, int left, int right) { // Hauptmethode der binären Suche // ... }

if (x == a[links] || x == a[rechts]) { return true; // Gefunden, true zurückgeben }

Wenn das Ergebnis von (rechts-links) eine negative Zahl ist, bedeutet dies, dass der Wert rechts kleiner ist als der Wert links.

int mid = (links+rechts)/2; //sonst: zwei Punkte

if(x == a[mid]) return true; // Das mittlere Element finden und true zurückgeben

else{ //sonst

Wenn x größer als das mittlere Element ist, geben Sie die binäre Suchfunktion (binarySearch) zurück und suchen Sie weiter nach x in der rechten Hälfte des Arrays (a), d. h. BinarySearch(a,x,mid+1,right) . Dies kann den Suchumfang einschränken und die Sucheffizienz verbessern.

else return binarySearch(a, x, left, mid-1); // Wenn der Zielwert kleiner als das mittlere Element ist, setze die Suche in der linken Hälfte fort.

}

}

public static final int[] sort(int[] a) { // Dies ist eine Methode zum Sortieren eines Arrays von Ganzzahlen // Sie können jeden Sortieralgorithmus verwenden, z. B. Blasensortierung, Einfügungssortierung, Auswahlsortierung, Schnellsortierung usw. // Hier verwenden wir Bubble Sort, um das Array zu sortieren for (int i = 0; i a[j + 1]) { // Elementpositionen tauschen int temp = a[j];

for (int i = 0; i

for (int j = 0; j

if(a[i]

swap(a,i,j);

}

}

}

zurückgeben;

}

private static void swap(int[] a, int i, int j) { //Definieren Sie eine private statische Funktion swap, um die Positionen der Elemente mit den Indizes i und j im Array a auszutauschen

int temp = a[i];

a[i] = a[j];

a[j] = temp;

}

public static void print(int[] a) { //Druckfunktion for (int i = 0; i

System.out.println();

for (int i = 0; i

System.out.print(a[i]);

if(i!=a.length-1) { System.out.print(","); }

}

System.out.println();

}

public static void main(String[] args) { //Testmethode

int[] a = {90, 12, 21, 32, 51, 78, 87, 98} ist ein Array mit 8 ganzen Zahlen.

print(sort(a));

System.out.println(binarySearch(sort(a), 40, 0, a.length-1)); ist ein Code, der für die binäre Suche nach Elementen mit einem Wert von 40 im sortierten Array a verwendet wird.

}

}

Das obige ist der detaillierte Inhalt vonBerechnen Sie den Schnittpunkt des Quadrats der Kurve y=x und der Geraden x=1 in Java mithilfe der Rekursion. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!