HTML5-Canvas-Zeichen-Tutorial (8) – BezierCurveTo-Methode zum Zeichnen von Kurven in Canvas_HTML5-Tutorial-Fähigkeiten

Im vorherigen Artikel habe ich über drei Methoden zum Zeichnen von Kurven in Canvas gesprochen: arc, arcTo und quadraticCurveTo Sie alle haben eines gemeinsam: Das heißt, die Kurven, die Sie zeichnen, können nur zu einer Seite verlaufen. Der größte Unterschied zwischen der bezierCurveTo, über die wir heute sprechen, und ihnen besteht darin, dass sie zwei Kontrollpunkte hat, was bedeutet, dass Sie eine S-förmige Kurve zeichnen können.

bezierCurveTo, auch Bezier-Kurve genannt, wenn Sie bestimmte Zeichenwerkzeuge erlernt haben, können Sie es sofort verstehen.
Die Syntax von bezierCurveTo lautet wie folgt:
ctx.bezierCurveTo(x1,y1,x2,y2,x,y); Ich werde seine Parameter wie üblich erklären, (x1,y1) ist Die Koordinaten von Kontrollpunkt 1, (x2, y2) sind die Koordinaten von Kontrollpunkt 2 und (x, y) sind die Koordinaten seines Endpunkts. Wie bei quadraticCurveTo werden auch seine Startpunktkoordinaten durch moveTo voreingestellt.

BezierCurveTo benötigt also 4 Punkte, um eine Kurve zu zeichnen: Startpunkt, Endpunkt, Kontrollpunkt 1, Kontrollpunkt 2. Für die nachfolgende Erklärung gehe ich hier davon aus, dass Kontrollpunkt 1 dem Startpunkt entspricht , und Kontrollpunkt 2 entspricht dem Endpunkt
Hier müssen wir das alte Problem des Leinwandzeichnens noch einmal erwähnen, das heißt, das Zeichnen des Codes basiert ausschließlich auf Vermutungen und Sie müssen eine Aktualisierung durchführen, um zu wissen, wo gezeichnet werden soll.

Ich werde die gute Tradition von zuvor fortsetzen und einige Hilfslinien zeichnen, um allen das Verständnis zu erleichtern:

Code kopieren

Der Code lautet wie folgt:

var x1=450, //x-Koordinate von Kontrollpunkt 1
y1 = 300, //y von Kontrollpunkt 1
x2 = 450, // x von Kontrollpunkt 2
y2 = 500, // y von Kontrollpunkt 2
x = 300, // Endpunkt x
y = 500; // Endpunkt y
ctx.moveTo(300,300) ;//Startpunkt
ctx.beginPath();
ctx.lineWidth = 5;
ctx.StrokeStyle = "rgba(0,0,0,1)"
ctx.moveTo(300,300) ;
ctx.bezierCurveTo(x1,y1,x2,y2,x,y);
ctx.Stroke();
//Hilfslinien zeichnen
ctx .beginPath();
ctx.StrokeStyle = "rgba(255,0,0,0.5)";
ctx.lineWidth = 1;
// Verbinden Sie den Startpunkt und den Kontrollpunkt 1
ctx.moveTo(300,300);
ctx.lineTo(x1,y1);
// Verbinden Sie den Endpunkt und Kontrollpunkt 2
ctx.moveTo(x2,y2); (x,y);
// Verbinden Sie den Startpunkt und den Endpunkt (Grundlinie)
ctx.moveTo(300,300);
ctx.lineTo(x,y); );

Hier zeichnen wir zunächst eine Kurve ähnlich quadraticCurveTo, die nur zu einer Seite geneigt ist. Diese Linie erscheint „glatt“, da die x-Koordinaten der Kontrollpunkte 1 und 2 gleich sind.

Zeichnen Sie nun eine weitere S-förmige Kurve, um zu beweisen, dass bezierCurveTo anders ist:

Code kopierenCode wie folgt:

var x1 = 150;

...

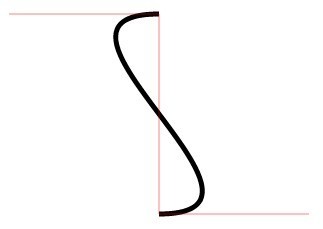Ändern Sie einfach die Koordinaten von Kontrollpunkt 1. Wenn die Koordinaten von Kontrollpunkt 1 und Kontrollpunkt 2 auf beiden Seiten der Grundlinie liegen, wird eine S-förmige Kurve gezeichnet. Liegen beide auf einer Seite der Grundlinie, hat dies einen ähnlichen Effekt wie bei quadraticCurveTo.

Die Situation in diesem Beispiel ist relativ einfach. Die Grundlinie (vom Startpunkt bis zum Endpunkt) ist jedoch in der Praxis meistens geneigt und die Situation ist viel komplizierter . Aber versuchen Sie es selbst

Jede Zeichenmethode scheint eine relativ einzelne Funktion zu haben, aber leistungsstarke Methoden sind die Kombination einzelner Methoden. In den folgenden Artikeln werde ich versuchen zu erklären, wie man einige herkömmliche Grafiken zeichnet, z. B. abgerundete Rechtecke und Ellipsen. Sie erfordern eine Kombination dieser vorherigen Einzelmethoden.