Heim >Technologie-Peripheriegeräte >KI >Erkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2)
Erkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2)
- PHPznach vorne
- 2023-11-20 17:25:411865Durchsuche

Im ersten Artikel dieser Serie haben wir die Zusammenhänge und Unterschiede zwischen künstlicher Intelligenz, maschinellem Lernen, Deep Learning, Data Science und anderen Bereichen diskutiert. Wir haben auch einige schwierige Entscheidungen hinsichtlich der Programmiersprachen, Tools und mehr getroffen, die in der gesamten Serie verwendet werden sollen. Abschließend haben wir noch ein wenig Matrixwissen eingeführt. In diesem Artikel werden wir die Matrix, den Kern der künstlichen Intelligenz, ausführlich besprechen. Aber vorher wollen wir zunächst die Geschichte der künstlichen Intelligenz verstehen.
Warum müssen wir die Geschichte der künstlichen Intelligenz verstehen? In der Geschichte gab es viele KI-Booms, aber in vielen Fällen blieben die großen Erwartungen an das Potenzial der KI aus. Das Verständnis der Geschichte der künstlichen Intelligenz kann uns helfen zu erkennen, ob diese Welle der künstlichen Intelligenz Wunder bewirken wird oder nur eine weitere Blase ist, die kurz vor dem Platzen steht.
Wann haben wir begonnen, den Ursprung der künstlichen Intelligenz zu verstehen? War es nach der Erfindung des Digitalcomputers? Oder früher? Ich glaube, dass das Streben nach einem allwissenden Wesen bis in die Anfänge der Zivilisation zurückreicht. Beispielsweise war Delphi in der antiken griechischen Mythologie ein Prophet, der jede Frage beantworten konnte. Auch die Suche nach kreativen Maschinen, die die menschliche Intelligenz übertreffen, fasziniert uns seit der Antike. Im Laufe der Geschichte gab es mehrere gescheiterte Versuche, Schachmaschinen zu bauen. Unter ihnen ist der berüchtigte Mechanical Turk, der kein echter Roboter ist, sondern von einem darin versteckten Schachspieler gesteuert wird. John Napiers Erfindung des Logarithmus, Blaise Pascals Taschenrechner und Charles Babbages Analytical Engine spielten alle eine Schlüsselrolle bei der Entwicklung der künstlichen Intelligenz. Was sind also die bisherigen Meilensteine in der Entwicklung der künstlichen Intelligenz? Wie bereits erwähnt, ist die Erfindung des digitalen Computers das wichtigste Ereignis in der Geschichte der Forschung zur künstlichen Intelligenz. Im Gegensatz zu elektromechanischen Geräten, deren Skalierbarkeit vom Leistungsbedarf abhängt, profitieren digitale Geräte von technologischen Fortschritten, beispielsweise von Vakuumröhren über Transistoren bis hin zu integrierten Schaltkreisen und jetzt VLSI.
Ein weiterer wichtiger Meilenstein in der Entwicklung der künstlichen Intelligenz ist Alan Turings erste theoretische Analyse der künstlichen Intelligenz. Er schlug den berühmten Turing-Test vor
In den späten 1950er Jahren schlug John McCarthy vor
In den 1970er und 1980er Jahren spielten Algorithmen in dieser Zeit eine wichtige Rolle. In dieser Zeit wurden viele neue effiziente Algorithmen vorgeschlagen. In den späten 1960er Jahren veröffentlichte Donald Knuth (ich empfehle Ihnen dringend, ihn kennenzulernen, in der Welt der Informatik entspricht er Gauss oder Euler in der Welt der Mathematik) die Veröffentlichung des ersten Bandes von „The Art of Computer Programming“. der Programmierung markierte den Beginn der Algorithmen-Ära. In diesen Jahren wurden viele Allzweckalgorithmen und Graphalgorithmen entwickelt. Darüber hinaus entstand zu dieser Zeit auch die Programmierung auf Basis künstlicher neuronaler Netze. Zwar gab es bereits in den 1940er Jahren Warren S. McCulloch und Walter Pitts
mindestens zwei vielversprechende Möglichkeiten für künstliche Intelligenz im digitalen Zeitalter, aber diese beiden Möglichkeiten entsprachen nicht den Erwartungen. Ist die aktuelle Welle der künstlichen Intelligenz ähnlich? Diese Frage ist schwer zu beantworten. Allerdings glaube ich persönlich, dass künstliche Intelligenz dieses Mal einen großen Einfluss haben wird (LCTT-Übersetzung: Dieser Artikel wurde im Juni 2022 veröffentlicht, ChatGTP wurde ein halbes Jahr später gestartet). Warum habe ich eine solche Vorhersage? Erstens ist Hochleistungsrechnerausrüstung mittlerweile günstig und leicht verfügbar. Gab es in den 1960er- und 1980er-Jahren nur wenige derart leistungsstarke Computergeräte, so verfügen wir heute über Millionen oder sogar Milliarden davon. Zweitens stehen mittlerweile riesige Datenmengen für das Training von Programmen für künstliche Intelligenz und maschinelles Lernen zur Verfügung. Stellen Sie sich vor, wie viele digitale Bildingenieure, die sich in den 1990er Jahren mit digitaler Bildverarbeitung beschäftigten, zum Trainieren von Algorithmen nutzen könnten? Vielleicht Tausende oder Zehntausende. Mittlerweile verfügt allein die Data-Science-Plattform Kaggle (eine Tochtergesellschaft von Google) über mehr als 10.000 Datensätze. Die riesigen Datenmengen, die das Internet täglich generiert, erleichtern das Training von Algorithmen. Drittens erleichtern Hochgeschwindigkeits-Internetverbindungen die Zusammenarbeit mit großen Institutionen. Im ersten Jahrzehnt des 21. Jahrhunderts war die Zusammenarbeit zwischen Informatikern schwierig. Die Geschwindigkeit des Internets macht jedoch mittlerweile die Zusammenarbeit mit Projekten der künstlichen Intelligenz wie Google Colab, Kaggle und Project Jupiter möglich. Basierend auf diesen drei Faktoren glaube ich, dass künstliche Intelligenz dieses Mal für immer existieren wird und es viele hervorragende Anwendungen geben wird
Mehr Wissen über Matrizen
Abbildung 1: Matrix A, B, C, D Nachdem wir die Geschichte der künstlichen Intelligenz verstanden haben, ist es nun an der Zeit, zum Thema Matrizen und Vektoren zurückzukehren. Ich habe sie in früheren Artikeln kurz vorgestellt. Dieses Mal tauchen wir tiefer in die Welt der Matrix ein. Schauen Sie sich bitte zunächst Abbildung 1 und Abbildung 2 an, die insgesamt 8 Matrizen von A bis H zeigen. Warum werden in Tutorials zu künstlicher Intelligenz und maschinellem Lernen so viele Matrizen benötigt? Erstens sind Matrizen, wie bereits erwähnt, der Kern der linearen Algebra, und die lineare Algebra ist nicht das Gehirn des maschinellen Lernens, aber der Kern des maschinellen Lernens. Zweitens hat in der folgenden Diskussion jede Matrix einen bestimmten Zweck Sehen wir uns an, wie Matrizen dargestellt werden und wie man ihre Details erhält. Abbildung 3 zeigt, wie Matrix A mit NumPy dargestellt wird. Obwohl Matrizen und Arrays nicht genau gleich sind, verwenden wir sie in praktischen Anwendungen oft als Synonyme. Hintergrundfarbe: rgb(231, 243, 237); padding: 1px 3px; overflow-wrap: break-indent: 0px;">array Funktion erstellt Matrix. Obwohl NumPy auch Folgendes bietet: 现在我们来做一些基本的矩阵运算。图 5 显示了如何将矩阵 A 和 B 相加。NumPy 提供了两种方法将矩阵相加, Abbildung 4: Größe, Dimension und Reihenfolge des Arrays Neuausdruck: Abbildung 5: Matrixsummierung 当然除了矩阵加法外还有其它矩阵运算。图 6 展示了矩阵减法和矩阵乘法。它们同样有两种形式,矩阵减法可以由 对于一个 m x n 阶和一个 p x q 阶的矩阵,当且仅当 n 等于 p 时它们才可以相乘,相乘的结果是一个 m x q 阶矩的阵。图 7 显示了更多矩阵相乘的示例。注意 到目前为止,我们都是通过键盘输入矩阵的。如果我们需要从文件或数据集中读取大型矩阵并处理,那该怎么办呢?这时我们就要用到另一个强大的 Python 库了——Pandas。我们以读取一个小的 CSV (逗号分隔值comma-separated value)文件为例。图 8 展示了如何读取 图 8:用 Pandas 读取 CSV 文件 需要进行改写的内容是:矩阵的秩 Dies ist das Ende dieses Inhalts. Im nächsten Artikel werden wir die Werkzeugbibliothek erweitern, damit sie zur Entwicklung von Programmen für künstliche Intelligenz und maschinelles Lernen verwendet werden können. Wir werden auch ausführlicher auf neuronale Netze, überwachtes Lernen und unüberwachtes Lernen eingehen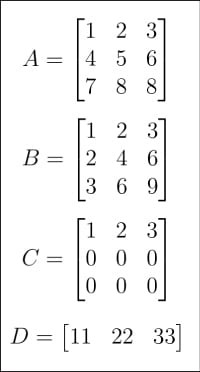
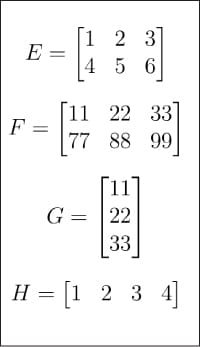 Abbildung 2: Matrizen E, F, G, H
Abbildung 2: Matrizen E, F, G, H 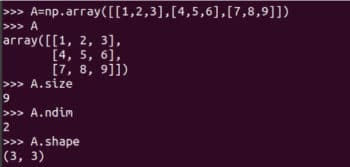 Abbildung 3: Darstellung der Matrix A in NumPy.
Abbildung 3: Darstellung der Matrix A in NumPy. matrix-Funktion zum Erstellen zweidimensionaler Arrays und Matrizen. Es wird jedoch in Zukunft veraltet sein, sodass seine Verwendung nicht mehr empfohlen wird. Einige Details der Matrix A sind auch in Abbildung 3 dargestellt. A.size gibt uns die Anzahl der Elemente im Array an. In unserem Fall ist es 9. Code A.nidm stellt die Dimension des Arrays dar. Es ist leicht zu erkennen, dass Matrix A zweidimensional ist. A.shape stellt die Reihenfolge der Matrix A dar. Die Reihenfolge der Matrix ist die Anzahl der Zeilen und Spalten der Matrix. Ich werde es zwar nicht näher erläutern, aber Sie müssen sich der Größe, Dimension und Reihenfolge Ihrer Matrizen bewusst sein, wenn Sie die NumPy-Bibliothek verwenden. Abbildung 4 zeigt, warum Größe, Dimension und Reihenfolge einer Matrix sorgfältig identifiziert werden sollten. Kleine Unterschiede in der Definition eines Arrays können zu Unterschieden in seiner Größe, Dimensionalität und Reihenfolge führen. Daher sollten Programmierer bei der Definition von Matrizen besonders auf diese Details achten. array 函数创建矩阵。虽然 NumPy 也提供了 matrix 函数来创建二维数组和矩阵。但是它将在未来被废弃,所以不再建议使用了。在图 3 还显示了矩阵 A 的一些详细信息。A.size 告诉我们数组中元素的个数。在我们的例子中,它是 9。代码 A.nidm 表示数组的 维数dimension。很容易看出矩阵 A 是二维的。A.shape 表示矩阵 A 的阶数order,矩阵的阶数是矩阵的行数和列数。虽然我不会进一步解释,但使用 NumPy 库时需要注意矩阵的大小、维度和阶数。图 4 显示了为什么应该仔细识别矩阵的大小、维数和阶数。定义数组时的微小差异可能导致其大小、维数和阶数的不同。因此,程序员在定义矩阵时应该格外注意这些细节。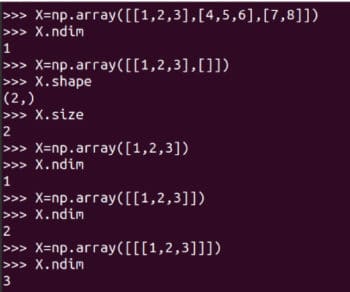 图 4:数组的大小、维数和阶数
图 4:数组的大小、维数和阶数add 函数和 +
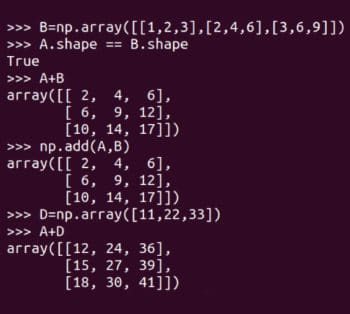 Jetzt führen wir einige grundlegende Matrixoperationen durch. Abbildung 5 zeigt, wie die Matrizen A und B addiert werden. NumPy bietet zwei Methoden zum Hinzufügen von Matrizen:
Jetzt führen wir einige grundlegende Matrixoperationen durch. Abbildung 5 zeigt, wie die Matrizen A und B addiert werden. NumPy bietet zwei Methoden zum Hinzufügen von Matrizen: add function and + Operator. Beachten Sie, dass nur Matrizen derselben Reihenfolge hinzugefügt werden können. Beispielsweise können zwei 4 × 3-Matrizen hinzugefügt werden, eine 3 × 4-Matrix und eine 2 × 3-Matrix können jedoch nicht hinzugefügt werden. Da sich die Programmierung jedoch von der Mathematik unterscheidet, folgt NumPy dieser Regel nicht. Abbildung 5 zeigt auch das Hinzufügen der Matrizen A und D. Denken Sie daran, dass diese Art der Matrixaddition mathematisch illegal ist. Einer heißt BroadcastingA.shape == B.shape
🎜Der Broadcasting-Mechanismus ist nicht allmächtig, wenn Sie versuchen, die Matrizen D und H zu addieren. Es tritt ein Betriebsfehler auf. 🎜subtract 函数或减法运算符 - 来实现,矩阵乘法可以由 matmul 函数或矩阵乘法运算符 @ 来实现。图 6 还展示了 逐元素乘法element-wise multiplication 运算符 * 的使用。请注意,只有 NumPy 的 matmul 函数和 @ 运算符执行的是数学意义上的矩阵乘法。在处理矩阵时要小心使用 * 运算符。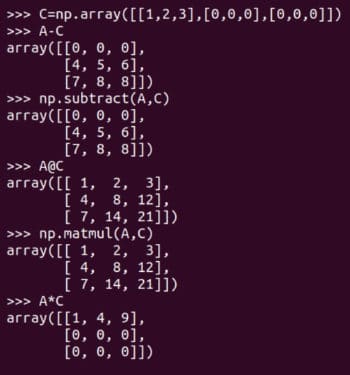 图 6:更多矩阵运算
图 6:更多矩阵运算E@A 是可行的,而 A@E 会导致错误。请仔细阅读对比 D@G 和 G@D 的示例。使用 shape 属性,确定这 8 个矩阵中哪些可以相乘。虽然根据严格的数学定义,矩阵是二维的,但我们将要处理更高维的数组。作为例子,下面的代码创建一个名为 T 的三维数组。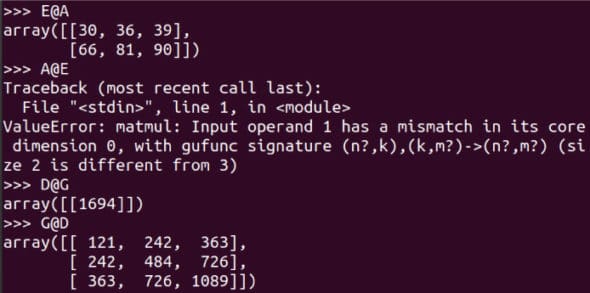 图 7:更多矩阵乘法的例子
图 7:更多矩阵乘法的例子T = np.array([[[11,22], [33,44]], [[55,66], [77,88]]])
Pandas
cricket.csv 文件,并将其中的前三行打印到终端上。在本系列的后续文章中将会介绍 Pandas 的更多特性。 图 8:用 Pandas 读取 CSV 文件
图 8:用 Pandas 读取 CSV 文件矩阵的秩
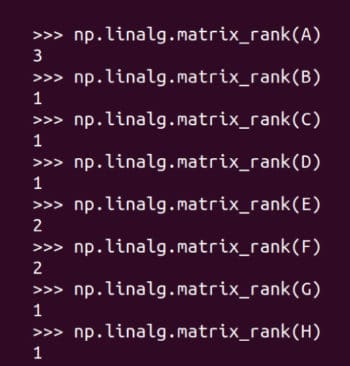 Abbildung 9: Ermitteln des Rangs der Matrix
Abbildung 9: Ermitteln des Rangs der Matrix
Das obige ist der detaillierte Inhalt vonErkundung der Geschichte und Matrix der künstlichen Intelligenz: Tutorial zur künstlichen Intelligenz (2). Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

