Heim >Technologie-Peripheriegeräte >KI >Neuer ungefährer Aufmerksamkeitsmechanismus HyperAttention: freundlich zu langen Kontexten, beschleunigt die LLM-Inferenz um 50 %
Neuer ungefährer Aufmerksamkeitsmechanismus HyperAttention: freundlich zu langen Kontexten, beschleunigt die LLM-Inferenz um 50 %
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-11-13 20:29:09859Durchsuche
Transformer war bei einer Vielzahl von Lernaufgaben in Bereichen wie der Verarbeitung natürlicher Sprache, Computer Vision und Zeitreihenvorhersage erfolgreich. Trotz ihres Erfolgs weisen diese Modelle immer noch erhebliche Einschränkungen in der Skalierbarkeit auf. Der Grund dafür ist, dass die genaue Berechnung der Aufmerksamkeitsschicht zu einer quadratischen (in der Sequenzlänge) Laufzeit und Speicherkomplexität führt. Dies bringt grundlegende Herausforderungen für die Erweiterung des Transformer-Modells auf längere Kontextlängen mit sich
Die Industrie hat verschiedene Methoden untersucht, um das Problem der quadratischen zeitlichen Aufmerksamkeitsschicht zu lösen, und eine der bemerkenswerten Richtungen ist die ungefähre Aufmerksamkeitszwischenmatrix in der Kraftschicht. Zu den Methoden, um dies zu erreichen, gehören die Approximation über dünn besetzte Matrizen, Matrizen mit niedrigem Rang oder eine Kombination aus beidem.
Allerdings bieten diese Methoden keine End-to-End-Garantien für die Approximation der Aufmerksamkeits-Output-Matrix. Diese Methoden zielen darauf ab, die einzelnen Aufmerksamkeitskomponenten schneller zu approximieren, aber keine bietet eine durchgängige Annäherung an die gesamte Skalarproduktaufmerksamkeit. Diese Methoden unterstützen auch nicht die Verwendung von Kausalmasken, die ein wichtiger Bestandteil moderner Transformer-Architekturen sind. Aktuelle theoretische Grenzen deuten darauf hin, dass es im Allgemeinen nicht möglich ist, eine termweise Annäherung der Aufmerksamkeitsmatrix in subquadratischer Zeit durchzuführen
Eine aktuelle Studie namens KDEFormer zeigt jedoch, dass, wenn die Aufmerksamkeitsmatrixterme begrenzt sind. Unter den Annahmen von , es kann nachweisbare Näherungen in subquadratischer Zeit liefern. Theoretisch beträgt die Laufzeit von KDEFormer ca. Aktuellen KDE-Algorithmen mangelt es jedoch an praktischer Effizienz, und selbst theoretisch besteht eine Lücke zwischen der Laufzeit von KDEFormer und einem theoretisch realisierbaren O(n)-Zeitalgorithmus. In dem Artikel beweist der Autor, dass unter der gleichen Annahme eines begrenzten Eintrags ein nahezu linearer Zeitalgorithmus möglich ist. Ihr Algorithmus beinhaltet jedoch auch die Verwendung von Polynommethoden zur Annäherung an den Softmax, was wahrscheinlich unpraktisch ist. 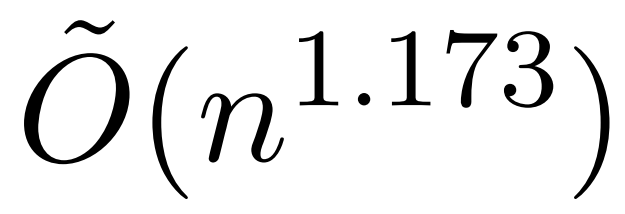 In diesem Artikel stellen Forscher der Yale University, Google Research und anderer Institutionen einen Algorithmus vor, der das Beste aus beiden Welten vereint, praktisch und effizient ist und die beste nahezu lineare Zeitgarantie erreichen kann. Darüber hinaus unterstützt die Methode eine kausale Maskierung, die in früheren Arbeiten nicht möglich war.
In diesem Artikel stellen Forscher der Yale University, Google Research und anderer Institutionen einen Algorithmus vor, der das Beste aus beiden Welten vereint, praktisch und effizient ist und die beste nahezu lineare Zeitgarantie erreichen kann. Darüber hinaus unterstützt die Methode eine kausale Maskierung, die in früheren Arbeiten nicht möglich war. 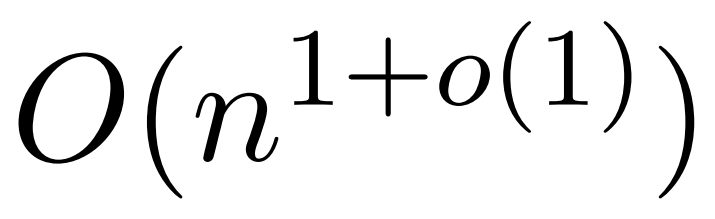
Bitte klicken Sie auf den folgenden Link, um das Papier anzuzeigen: https://arxiv.org/abs/2310.05869

Wie folgt umgeschrieben: Die Forscher führten zwei zu messende Parameter ein: (1) die maximale Spaltennorm der normalisierten Aufmerksamkeitsmatrix, (2) der Anteil der Zeilennormen in der nicht normalisierten Aufmerksamkeitsmatrix nach dem Entfernen großer Einträge. Sie verwenden diese feinkörnigen Parameter, um die Schwierigkeit des Problems widerzuspiegeln. Solange die oben genannten Parameter klein sind, kann der lineare Zeitabtastalgorithmus auch dann implementiert werden, wenn die Matrix unbegrenzte Einträge oder einen großen stabilen Rang aufweist.
HyperAttention weist die Merkmale eines modularen Designs auf und kann problemlos in andere schnelle zugrunde liegende Implementierungen integriert werden , insbesondere Es ist FlashAttention. Empirisch gesehen übertrifft Super Attention bestehende Methoden bei der Verwendung des LSH-Algorithmus zur Identifizierung großer Einträge und erzielt erhebliche Geschwindigkeitsverbesserungen im Vergleich zu modernen Lösungen wie FlashAttention. Forscher überprüften die Leistung von HyperAttention anhand einer Vielzahl von Kontextdatensätzen unterschiedlicher Länge
Beispielsweise verkürzte HyperAttention die Inferenzzeit von ChatGLM2 bei einer Kontextlänge von 32 KB um 50 %, während die Ratlosigkeit von 5,6 auf 6,3 stieg. HyperAttention ist auf einer einzelnen Aufmerksamkeitsebene mit größeren Kontextlängen (z. B. 131 KB) und Kausalmasken 5x schneller.
Methodenübersicht
Punktproduktaufmerksamkeit umfasst die Verarbeitung von drei Eingabematrizen: Q (Abfragen), K (Schlüssel), V (Wert), alle von der Größe nxd, wobei n die Anzahl der Token in der Eingabesequenz ist , d ist die Dimensionalität der zugrunde liegenden Darstellung. Das Ergebnis dieses Prozesses ist wie folgt:
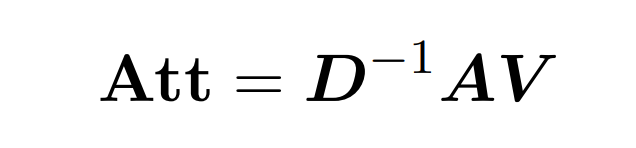
Hier wird Matrix A := exp (QK^T) als Elementindex von QK^T definiert. D ist eine n×n-Diagonalmatrix, abgeleitet aus der Summe der Zeilen von A, wobei 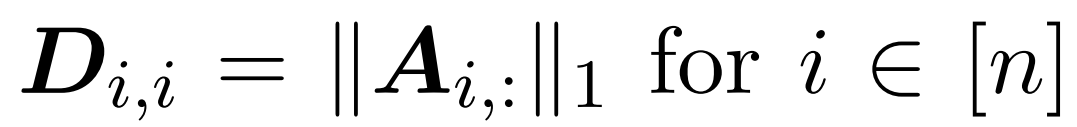 . In diesem Fall wird Matrix A als „Aufmerksamkeitsmatrix“ und (D^-1) A als „Softmax-Matrix“ bezeichnet. Es ist erwähnenswert, dass die direkte Berechnung der Aufmerksamkeitsmatrix A Θ(n²d) Operationen erfordert, während das Speichern Θ(n²) Speicher verbraucht. Daher erfordert die direkte Berechnung von Att Ω(n²d) Laufzeit und Ω(n²) Speicher.
. In diesem Fall wird Matrix A als „Aufmerksamkeitsmatrix“ und (D^-1) A als „Softmax-Matrix“ bezeichnet. Es ist erwähnenswert, dass die direkte Berechnung der Aufmerksamkeitsmatrix A Θ(n²d) Operationen erfordert, während das Speichern Θ(n²) Speicher verbraucht. Daher erfordert die direkte Berechnung von Att Ω(n²d) Laufzeit und Ω(n²) Speicher.
Das Ziel des Forschers besteht darin, die Ausgangsmatrix Att effizient anzunähern und gleichzeitig ihre spektralen Eigenschaften beizubehalten. Ihre Strategie besteht darin, einen nahezu linearen zeiteffizienten Schätzer für die diagonal skalierende Matrix D zu entwerfen. Darüber hinaus nähern sie sich durch Unterabtastung schnell dem Matrixprodukt der Softmax-Matrix D^-1A an. Genauer gesagt zielen sie darauf ab, eine Stichprobenmatrix 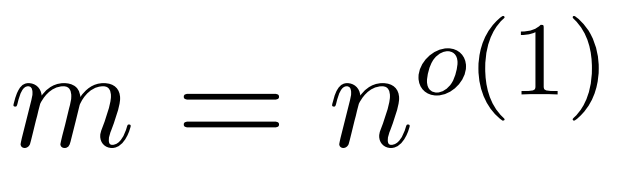 mit einer endlichen Anzahl von Zeilen
mit einer endlichen Anzahl von Zeilen 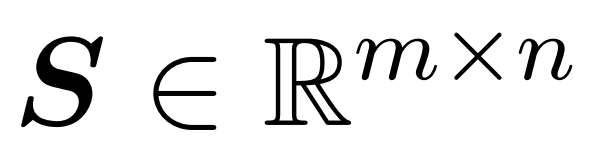 und einer Diagonalmatrix
und einer Diagonalmatrix 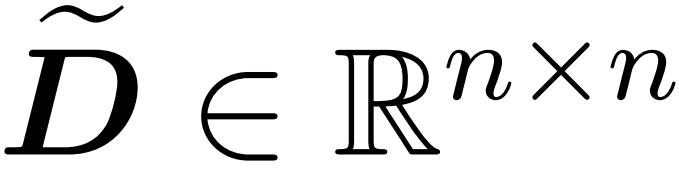 zu finden, sodass die folgenden Einschränkungen für die Operatorspezifikation des Fehlers erfüllt sind:
zu finden, sodass die folgenden Einschränkungen für die Operatorspezifikation des Fehlers erfüllt sind:
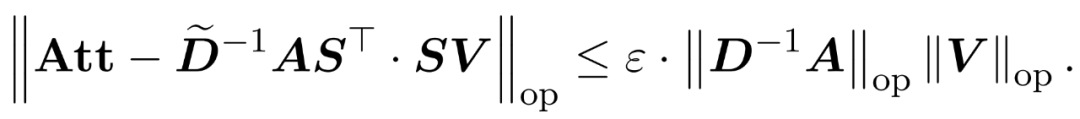
Forscher haben gezeigt, dass durch die Definition der Stichprobenmatrix S basierend auf der Zeilenspezifikation von V der Matrixmultiplikationsteil des Aufmerksamkeitsnäherungsproblems in Formel (1) effizient gelöst werden kann. Das anspruchsvollere Problem besteht darin, wie man eine zuverlässige Näherung der Diagonalmatrix D erhält. In aktuellen Ergebnissen nutzt Zandieh den schnellen KDE-Löser effektiv aus, um qualitativ hochwertige Näherungen von D zu erhalten. Wir haben das KDEformer-Programm vereinfacht und gezeigt, dass eine gleichmäßige Abtastung ausreicht, um die erforderlichen spektralen Garantien zu erreichen, ohne dass eine Kerndichte-basierte Wichtigkeitsabtastung erforderlich ist. Diese erhebliche Vereinfachung ermöglichte es ihnen, einen praktischen, nachweisbaren linearen Zeitalgorithmus zu entwickeln.
Im Gegensatz zu früheren Untersuchungen erfordert unsere Methode keine begrenzten Einträge oder begrenzten stabilen Ränge. Selbst wenn die Einträge in der Aufmerksamkeitsmatrix oder im stabilen Rang groß sind, können die zur Analyse der Zeitkomplexität eingeführten feinkörnigen Parameter weiterhin klein sein.
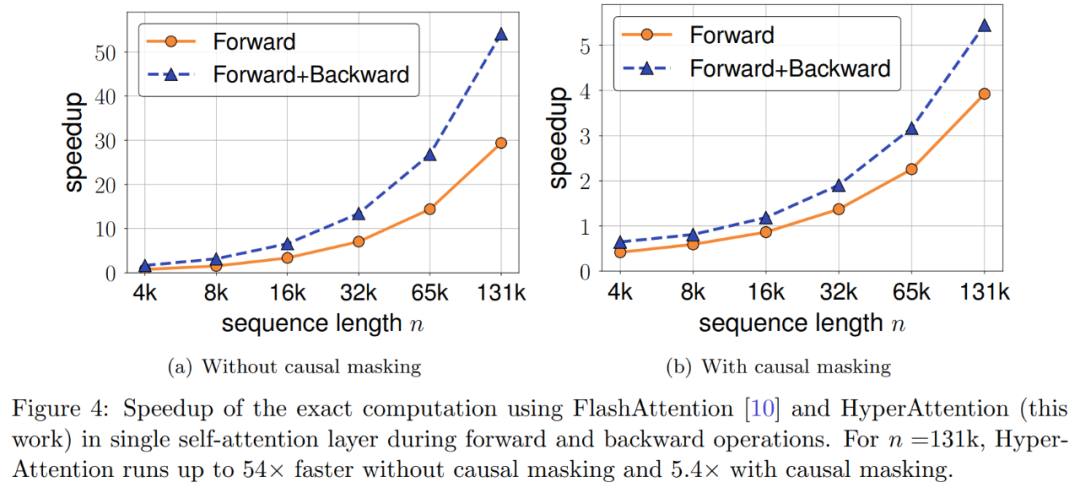
Dadurch ist HyperAttention deutlich schneller, mit einer über 50-mal schnelleren Vorwärts- und Rückwärtsausbreitung bei einer Sequenzlänge von n=131k. Beim Umgang mit Kausalmasken erreicht die Methode immer noch eine erhebliche 5-fache Geschwindigkeitssteigerung. Wenn die Methode außerdem auf ein vorab trainiertes LLM (z. B. chatqlm2-6b-32k) angewendet und anhand des Langkontext-Benchmark-Datensatzes LongBench ausgewertet wird, behält sie ein Leistungsniveau nahe dem Originalmodell bei, auch ohne dass eine Feinabstimmung erforderlich ist . Die Forscher bewerteten auch spezifische Aufgaben und stellten fest, dass Zusammenfassungs- und Code-Vervollständigungsaufgaben einen größeren Einfluss auf die ungefähren Aufmerksamkeitsebenen hatten als Aufgaben zur Problemlösung.
Algorithmus
Um eine Spektrumsgarantie bei der Approximation von Att zu erhalten, besteht der erste Schritt in diesem Artikel darin, eine 1 ± ε-Approximation für die Diagonalterme der Matrix D durchzuführen. Anschließend wird das Matrixprodukt zwischen A und V durch Abtasten (D^-1) gemäß den Quadratzeilen-ℓ₂-Normen von V angenähert.
Der Prozess der Approximation von D besteht aus zwei Schritten. Zunächst wird ein Algorithmus, der auf Hammings Sortier-LSH basiert, verwendet, um die dominanten Einträge in der Aufmerksamkeitsmatrix zu identifizieren, wie in Definition 1 gezeigt. Der zweite Schritt besteht darin, eine kleine Teilmenge von K zufällig auszuwählen. In diesem Artikel wird gezeigt, dass diese einfache Methode unter bestimmten milden Annahmen zu den Matrizen A und D die spektralen Grenzen der geschätzten Matrizen ermitteln kann. Das Ziel des Forschers besteht darin, eine ungefähre Matrix D zu finden, die genau genug ist, um Folgendes zu erfüllen:

Die Annahme dieses Artikels ist, dass die Spaltennorm der Softmax-Matrix eine relativ gleichmäßige Verteilung aufweist. Genauer gesagt geht der Forscher davon aus, dass es für jedes i ∈ [n] t ein 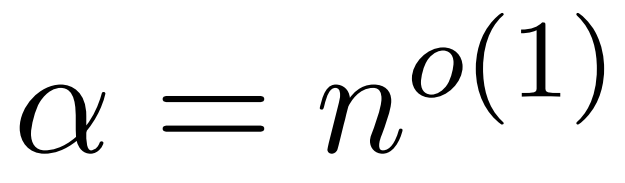 gibt, so dass
gibt, so dass 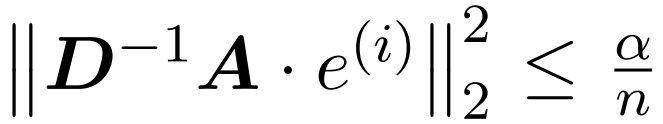 .
.
Der erste Schritt des Algorithmus besteht darin, große Einträge in der Aufmerksamkeitsmatrix A zu identifizieren, indem Schlüssel und Abfragen mithilfe von Hamming-sortiertem LSH (sortLSH) in Buckets einheitlicher Größe gehasht werden. Algorithmus 1 beschreibt diesen Prozess detailliert und Abbildung 1 veranschaulicht ihn visuell.
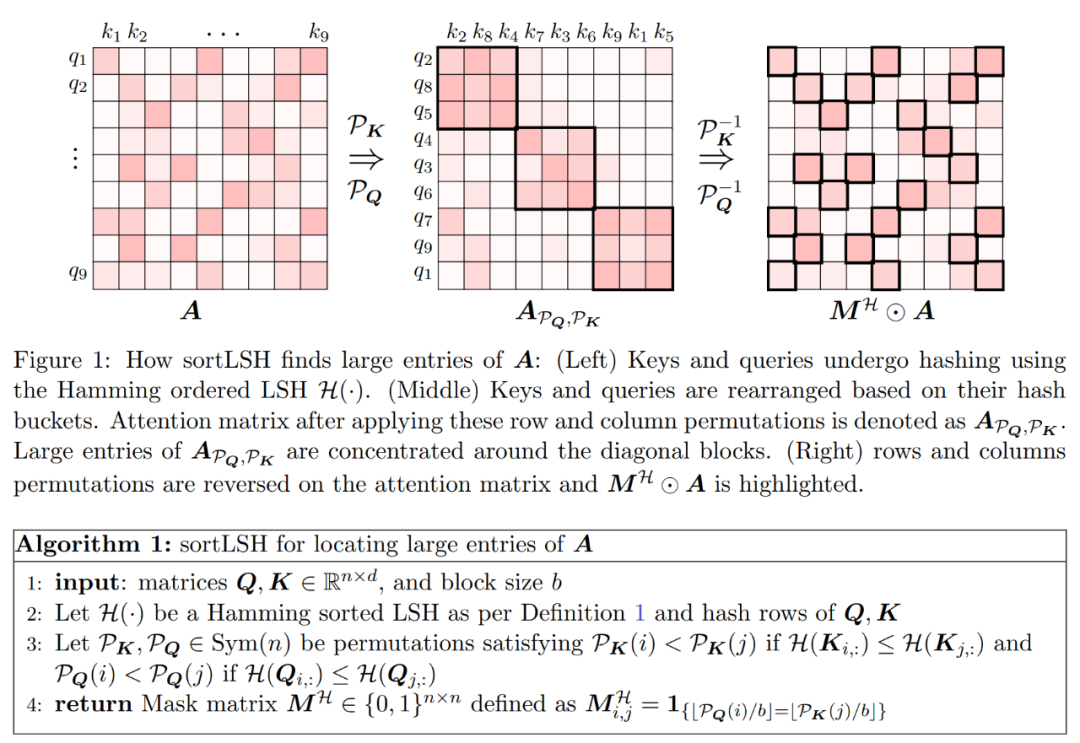
Die Funktion von Algorithmus 1 besteht darin, eine spärliche Maske zurückzugeben, die zum Isolieren der Haupteinträge der Aufmerksamkeitsmatrix verwendet wird. Nachdem er diese Maske erhalten hat, kann der Forscher eine Näherung der Matrix D in Algorithmus 2 berechnen, die die Spektralgarantie in Gleichung (2) erfüllt. Der Algorithmus wird implementiert, indem der der Maske entsprechende Aufmerksamkeitswert mit einem zufällig ausgewählten Satz von Spalten in der Aufmerksamkeitsmatrix kombiniert wird. Der Algorithmus in diesem Artikel kann breit angewendet und effizient eingesetzt werden, indem vordefinierte Masken verwendet werden, um die Position der Haupteinträge in der Aufmerksamkeitsmatrix festzulegen. Die Hauptgarantie des Algorithmus ist in Satz 1 gegeben. Eine Unterroutine, die die Näherungsdiagonale
und das Matrixprodukt zwischen der Näherungsdiagonale 
und der Wertematrix V integriert. Daher führten die Forscher HyperAttention ein, einen effizienten Algorithmus, der den Aufmerksamkeitsmechanismus in Formel (1) mit Spektrumgarantie in annähernd linearer Zeit annähern kann. Algorithmus 3 verwendet als Eingabe eine Maske MH, die die Position des dominanten Eintrags in der Aufmerksamkeitsmatrix definiert. Diese Maske kann mit dem sortLSH-Algorithmus (Algorithmus 1) generiert werden oder eine vordefinierte Maske sein, ähnlich dem Ansatz in [7]. Wir gehen davon aus, dass die große Eintragsmaske M^H von Natur aus dünn besetzt ist und ihre Anzahl an Einträgen ungleich Null begrenzt ist
.
Wie in Abbildung 2 dargestellt, basiert diese Methode auf einer wichtigen Beobachtung. Die maskierte Aufmerksamkeit M^C⊙A kann in drei Matrizen ungleich Null zerlegt werden, von denen jede halb so groß ist wie die ursprüngliche Aufmerksamkeitsmatrix. Block A_21 liegt vollständig unterhalb der Diagonale und entlarvt die Aufmerksamkeit. Daher können wir seine Zeilensumme mit Algorithmus 2 approximieren. 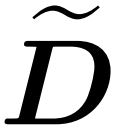 Die beiden diagonalen Blöcke
Die beiden diagonalen Blöcke 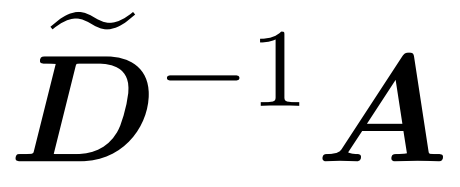 und
und 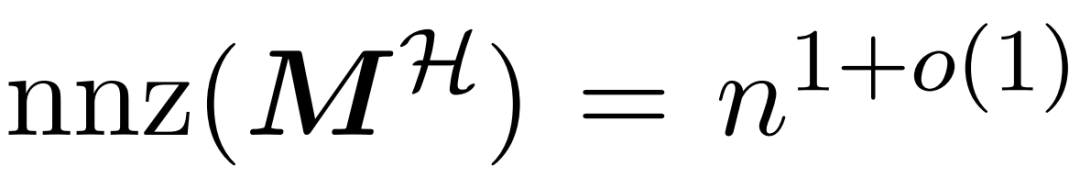 in Abbildung 2 sind kausale Aufmerksamkeiten, die halb so groß sind wie ursprünglich. Um mit diesen kausalen Zusammenhängen umzugehen, verwendeten die Forscher einen rekursiven Ansatz, indem sie sie weiter in kleinere Teile aufteilten und den Vorgang wiederholten. Der Pseudocode für diesen Prozess ist in Algorithmus 4 angegeben.
in Abbildung 2 sind kausale Aufmerksamkeiten, die halb so groß sind wie ursprünglich. Um mit diesen kausalen Zusammenhängen umzugehen, verwendeten die Forscher einen rekursiven Ansatz, indem sie sie weiter in kleinere Teile aufteilten und den Vorgang wiederholten. Der Pseudocode für diesen Prozess ist in Algorithmus 4 angegeben.
Experimente und Ergebnisse Die Forscher haben den Algorithmus einem Benchmarking unterzogen, indem sie das vorhandene große Sprachmodell erweitert haben, um Sequenzen mit großer Reichweite zu verarbeiten. Alle Experimente wurden auf einer einzelnen 40-GB-A100-GPU ausgeführt und FlashAttention 2 zur präzisen Aufmerksamkeitsberechnung verwendet.
Die Forscher haben den Algorithmus einem Benchmarking unterzogen, indem sie das vorhandene große Sprachmodell erweitert haben, um Sequenzen mit großer Reichweite zu verarbeiten. Alle Experimente wurden auf einer einzelnen 40-GB-A100-GPU ausgeführt und FlashAttention 2 zur präzisen Aufmerksamkeitsberechnung verwendet. 
Um die ursprüngliche Bedeutung unverändert beizubehalten, muss der Inhalt ins Chinesische umgeschrieben werden und der ursprüngliche Satz muss nicht erscheinen
Die Forscher bewerteten HyperAttention zunächst auf zwei vorab trainierten LLMs und wählte das Modell aus, das in praktischen Anwendungen weit verbreitet ist: chatglm2-6b-32k und phi-1.5.
Im Betrieb patchen sie die letzte ℓ-Aufmerksamkeitsschicht, indem sie sie durch HyperAttention ersetzen, wobei die Anzahl der ℓ von 0 bis zur Gesamtzahl aller Aufmerksamkeitsschichten in jedem LLM variieren kann. Beachten Sie, dass die Aufmerksamkeit in beiden Modellen eine kausale Maske erfordert und Algorithmus 4 rekursiv angewendet wird, bis die Eingabesequenzlänge n weniger als 4.096 beträgt. Für alle Sequenzlängen legen wir die Bucket-Größe b und die Anzahl der abgetasteten Spalten m auf 256 fest. Sie bewerteten die Leistung solcher Monkey-Patch-Modelle im Hinblick auf Verwirrung und Beschleunigung.
Gleichzeitig verwendeten die Forscher LongBench, eine Sammlung von Benchmark-Datensätzen mit langem Kontext, die 6 verschiedene Aufgaben enthält, nämlich Beantwortung von Einzel-/Mehrdokument-Fragen, Zusammenfassung, Lernen kleiner Stichproben, Syntheseaufgaben und Code-Vervollständigung. Sie wählten eine Teilmenge des Datensatzes mit einer Codierungssequenzlänge von mehr als 32.768 aus und beschnitten sie, wenn die Länge 32.768 überschritt. Berechnen Sie dann die Verwirrung jedes Modells, d. h. den Verlust bei der Vorhersage des nächsten Tokens. Um die Skalierbarkeit für lange Sequenzen hervorzuheben, haben wir auch die Gesamtbeschleunigung über alle Aufmerksamkeitsebenen berechnet, unabhängig davon, ob sie von HyperAttention oder FlashAttention durchgeführt wird.
Die in Abbildung 3 oben gezeigten Ergebnisse sind wie folgt. Auch wenn chatglm2-6b-32k den HyperAttention-Affenpatch bestanden hat, zeigt es immer noch ein angemessenes Maß an Verwirrung. Nach dem Ersetzen von Schicht 20 erhöht sich die Perplexität beispielsweise um etwa 1 und steigt langsam weiter an, bis Schicht 24 erreicht wird. Die Laufzeit der Aufmerksamkeitsschicht wurde um ca. 50 % verbessert. Wenn alle Schichten ausgetauscht werden, steigt die Perplexität auf 12 und läuft 2,3-mal schneller. Das Phi-1,5-Modell zeigt ebenfalls eine ähnliche Situation, aber mit zunehmender HyperAttention nimmt die Verwirrung linear zu
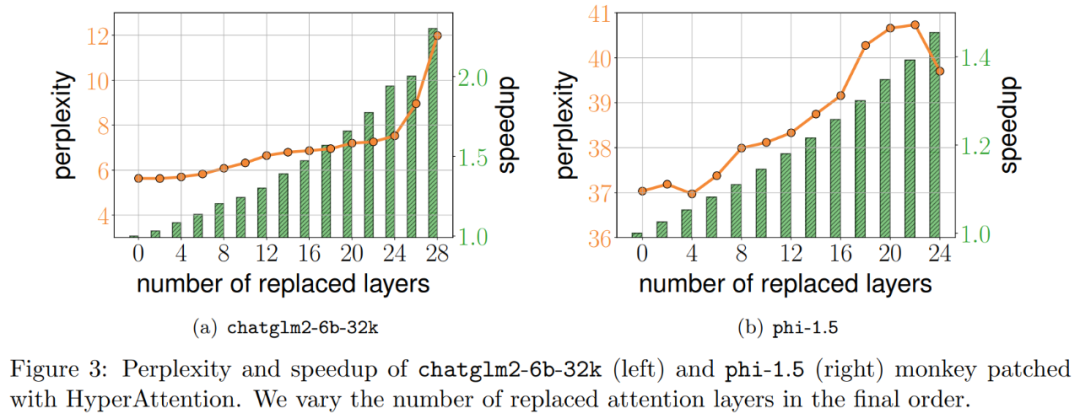
Darüber hinaus führten die Forscher auch Monkey Patched Chatglm2-6b-32k am LongBench-Datensatz durch Es wurde eine Leistungsbewertung durchgeführt und die Bewertungsergebnisse für die jeweiligen Aufgaben wie Beantwortung einzelner/mehrerer Dokumentfragen, Zusammenfassung, Lernen kleiner Stichproben, Syntheseaufgaben und Codevervollständigung berechnet. Die Bewertungsergebnisse sind in Tabelle 1 unten aufgeführt.
Während das Ersetzen von HyperAttention normalerweise zu einer Leistungseinbuße führt, stellten sie fest, dass die Auswirkungen je nach anstehender Aufgabe unterschiedlich sind. Beispielsweise sind Zusammenfassung und Code-Vervollständigung im Vergleich zu anderen Aufgaben am robustesten.
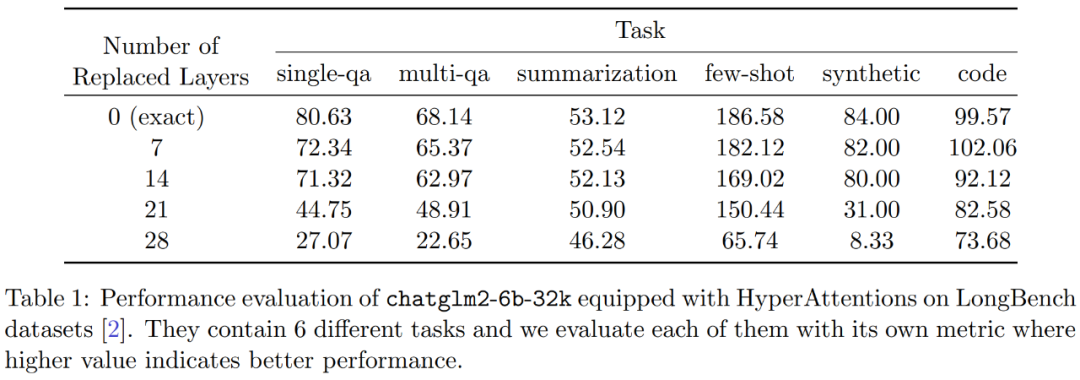
Das Bemerkenswerte ist, dass die Forscher bestätigten, dass der Leistungsabfall für die meisten Aufgaben 13 % nicht überschreiten wird, wenn die Hälfte der Aufmerksamkeitsschichten (d. h. 14 Schichten) gepatcht werden. Insbesondere bei der Zusammenfassungsaufgabe bleibt die Leistung nahezu unverändert, was darauf hinweist, dass diese Aufgabe am robustesten gegenüber teilweisen Änderungen im Aufmerksamkeitsmechanismus ist. Bei n = 32k erhöht sich die Berechnungsgeschwindigkeit der Aufmerksamkeitsschicht um das 1,5-fache.
Einzelne Selbstaufmerksamkeitsschicht
Die Forscher untersuchten die Beschleunigung von HyperAttention weiter, wenn die Sequenzlänge zwischen 4.096 und 131.072 variierte. Sie haben die Gesamtzeit von Vorwärts- und Vorwärts- und Rückwärtsvorgängen gemessen, wenn sie mit FlashAttention berechnet oder mit HyperAttention beschleunigt wurden. Es wurde auch die Uhrzeit der Wanduhr mit und ohne Kausalmaskierung gemessen. Alle Eingaben Q, K und V haben die gleiche Länge, die Dimensionalität ist auf d = 64 festgelegt und die Anzahl der Aufmerksamkeitsköpfe beträgt 12.
Sie wählen die gleichen Parameter wie zuvor in HyperAttention. Wie in Abbildung 4 dargestellt, erhöht sich die Geschwindigkeit von HyperAttention um das 54-fache, wenn die Kausalmaske nicht angewendet wird, und mit der Kausalmaske wird die Geschwindigkeit um das 5,4-fache erhöht. Obwohl die zeitliche Verwirrung von Kausalmaskierung und Nichtmaskierung gleich ist, erfordert der eigentliche Algorithmus der Kausalmaskierung (Algorithmus 1) zusätzliche Operationen wie die Partitionierung von Q, K und V und die Zusammenführung von Aufmerksamkeitsausgaben, was zu einer Erhöhung der tatsächlichen Laufzeit führt. Wenn die Sequenzlänge n zunimmt, wird die Beschleunigung höher sein
Die Forscher glauben, dass diese Ergebnisse nicht nur auf Schlussfolgerungen anwendbar sind, sondern auch zum Trainieren oder Feinabstimmen von LLM verwendet werden können, um sich an längere Sequenzen anzupassen, was neue Möglichkeiten eröffnet die Erweiterung der Selbstaufmerksamkeit Neue Möglichkeiten
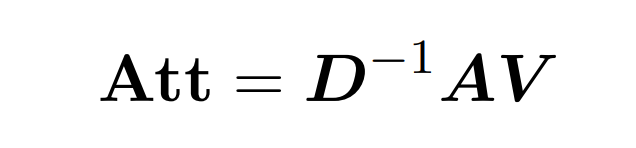
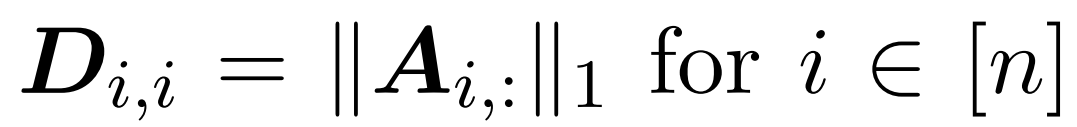 . In diesem Fall wird Matrix A als „Aufmerksamkeitsmatrix“ und (D^-1) A als „Softmax-Matrix“ bezeichnet. Es ist erwähnenswert, dass die direkte Berechnung der Aufmerksamkeitsmatrix A Θ(n²d) Operationen erfordert, während das Speichern Θ(n²) Speicher verbraucht. Daher erfordert die direkte Berechnung von Att Ω(n²d) Laufzeit und Ω(n²) Speicher.
. In diesem Fall wird Matrix A als „Aufmerksamkeitsmatrix“ und (D^-1) A als „Softmax-Matrix“ bezeichnet. Es ist erwähnenswert, dass die direkte Berechnung der Aufmerksamkeitsmatrix A Θ(n²d) Operationen erfordert, während das Speichern Θ(n²) Speicher verbraucht. Daher erfordert die direkte Berechnung von Att Ω(n²d) Laufzeit und Ω(n²) Speicher. 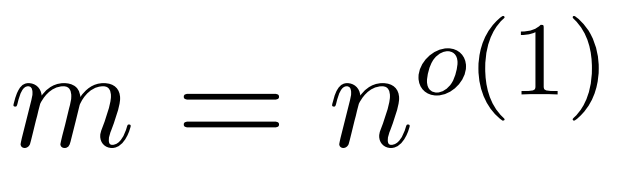 mit einer endlichen Anzahl von Zeilen
mit einer endlichen Anzahl von Zeilen 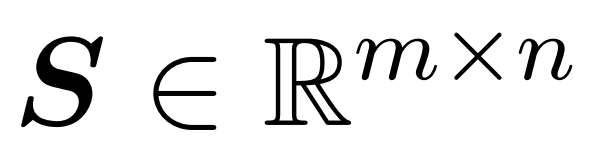 und einer Diagonalmatrix
und einer Diagonalmatrix 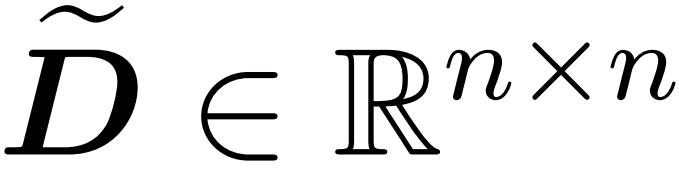 zu finden, sodass die folgenden Einschränkungen für die Operatorspezifikation des Fehlers erfüllt sind:
zu finden, sodass die folgenden Einschränkungen für die Operatorspezifikation des Fehlers erfüllt sind: 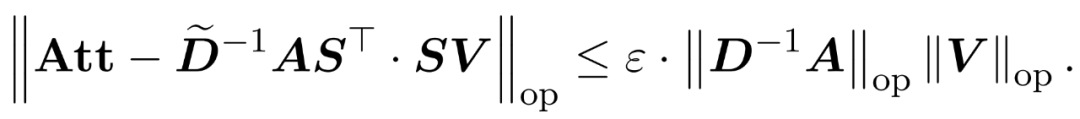

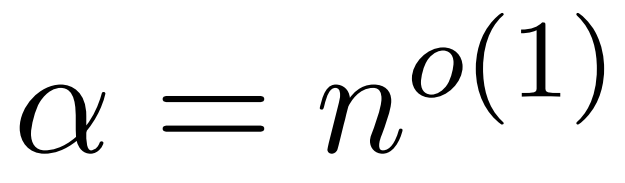 gibt, so dass
gibt, so dass 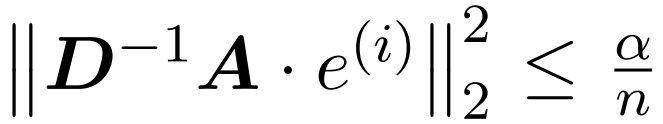 .
. 


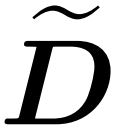 Die beiden diagonalen Blöcke
Die beiden diagonalen Blöcke 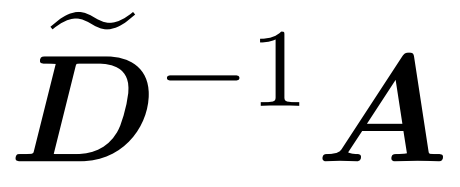 und
und 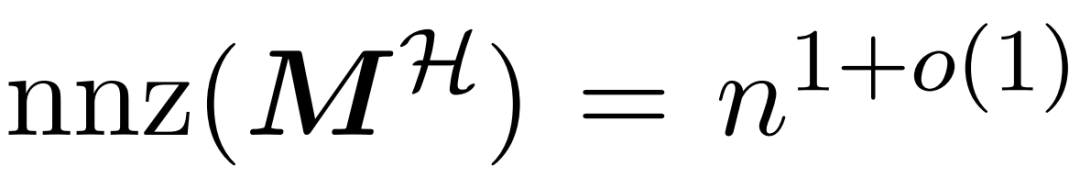 in Abbildung 2 sind kausale Aufmerksamkeiten, die halb so groß sind wie ursprünglich. Um mit diesen kausalen Zusammenhängen umzugehen, verwendeten die Forscher einen rekursiven Ansatz, indem sie sie weiter in kleinere Teile aufteilten und den Vorgang wiederholten. Der Pseudocode für diesen Prozess ist in Algorithmus 4 angegeben.
in Abbildung 2 sind kausale Aufmerksamkeiten, die halb so groß sind wie ursprünglich. Um mit diesen kausalen Zusammenhängen umzugehen, verwendeten die Forscher einen rekursiven Ansatz, indem sie sie weiter in kleinere Teile aufteilten und den Vorgang wiederholten. Der Pseudocode für diesen Prozess ist in Algorithmus 4 angegeben.  Die Forscher haben den Algorithmus einem Benchmarking unterzogen, indem sie das vorhandene große Sprachmodell erweitert haben, um Sequenzen mit großer Reichweite zu verarbeiten. Alle Experimente wurden auf einer einzelnen 40-GB-A100-GPU ausgeführt und FlashAttention 2 zur präzisen Aufmerksamkeitsberechnung verwendet.
Die Forscher haben den Algorithmus einem Benchmarking unterzogen, indem sie das vorhandene große Sprachmodell erweitert haben, um Sequenzen mit großer Reichweite zu verarbeiten. Alle Experimente wurden auf einer einzelnen 40-GB-A100-GPU ausgeführt und FlashAttention 2 zur präzisen Aufmerksamkeitsberechnung verwendet. 
Um die ursprüngliche Bedeutung unverändert beizubehalten, muss der Inhalt ins Chinesische umgeschrieben werden und der ursprüngliche Satz muss nicht erscheinen
Die Forscher bewerteten HyperAttention zunächst auf zwei vorab trainierten LLMs und wählte das Modell aus, das in praktischen Anwendungen weit verbreitet ist: chatglm2-6b-32k und phi-1.5.
Im Betrieb patchen sie die letzte ℓ-Aufmerksamkeitsschicht, indem sie sie durch HyperAttention ersetzen, wobei die Anzahl der ℓ von 0 bis zur Gesamtzahl aller Aufmerksamkeitsschichten in jedem LLM variieren kann. Beachten Sie, dass die Aufmerksamkeit in beiden Modellen eine kausale Maske erfordert und Algorithmus 4 rekursiv angewendet wird, bis die Eingabesequenzlänge n weniger als 4.096 beträgt. Für alle Sequenzlängen legen wir die Bucket-Größe b und die Anzahl der abgetasteten Spalten m auf 256 fest. Sie bewerteten die Leistung solcher Monkey-Patch-Modelle im Hinblick auf Verwirrung und Beschleunigung.
Gleichzeitig verwendeten die Forscher LongBench, eine Sammlung von Benchmark-Datensätzen mit langem Kontext, die 6 verschiedene Aufgaben enthält, nämlich Beantwortung von Einzel-/Mehrdokument-Fragen, Zusammenfassung, Lernen kleiner Stichproben, Syntheseaufgaben und Code-Vervollständigung. Sie wählten eine Teilmenge des Datensatzes mit einer Codierungssequenzlänge von mehr als 32.768 aus und beschnitten sie, wenn die Länge 32.768 überschritt. Berechnen Sie dann die Verwirrung jedes Modells, d. h. den Verlust bei der Vorhersage des nächsten Tokens. Um die Skalierbarkeit für lange Sequenzen hervorzuheben, haben wir auch die Gesamtbeschleunigung über alle Aufmerksamkeitsebenen berechnet, unabhängig davon, ob sie von HyperAttention oder FlashAttention durchgeführt wird.
Die in Abbildung 3 oben gezeigten Ergebnisse sind wie folgt. Auch wenn chatglm2-6b-32k den HyperAttention-Affenpatch bestanden hat, zeigt es immer noch ein angemessenes Maß an Verwirrung. Nach dem Ersetzen von Schicht 20 erhöht sich die Perplexität beispielsweise um etwa 1 und steigt langsam weiter an, bis Schicht 24 erreicht wird. Die Laufzeit der Aufmerksamkeitsschicht wurde um ca. 50 % verbessert. Wenn alle Schichten ausgetauscht werden, steigt die Perplexität auf 12 und läuft 2,3-mal schneller. Das Phi-1,5-Modell zeigt ebenfalls eine ähnliche Situation, aber mit zunehmender HyperAttention nimmt die Verwirrung linear zu

Darüber hinaus führten die Forscher auch Monkey Patched Chatglm2-6b-32k am LongBench-Datensatz durch Es wurde eine Leistungsbewertung durchgeführt und die Bewertungsergebnisse für die jeweiligen Aufgaben wie Beantwortung einzelner/mehrerer Dokumentfragen, Zusammenfassung, Lernen kleiner Stichproben, Syntheseaufgaben und Codevervollständigung berechnet. Die Bewertungsergebnisse sind in Tabelle 1 unten aufgeführt.
Während das Ersetzen von HyperAttention normalerweise zu einer Leistungseinbuße führt, stellten sie fest, dass die Auswirkungen je nach anstehender Aufgabe unterschiedlich sind. Beispielsweise sind Zusammenfassung und Code-Vervollständigung im Vergleich zu anderen Aufgaben am robustesten.

Das Bemerkenswerte ist, dass die Forscher bestätigten, dass der Leistungsabfall für die meisten Aufgaben 13 % nicht überschreiten wird, wenn die Hälfte der Aufmerksamkeitsschichten (d. h. 14 Schichten) gepatcht werden. Insbesondere bei der Zusammenfassungsaufgabe bleibt die Leistung nahezu unverändert, was darauf hinweist, dass diese Aufgabe am robustesten gegenüber teilweisen Änderungen im Aufmerksamkeitsmechanismus ist. Bei n = 32k erhöht sich die Berechnungsgeschwindigkeit der Aufmerksamkeitsschicht um das 1,5-fache.
Einzelne Selbstaufmerksamkeitsschicht
Die Forscher untersuchten die Beschleunigung von HyperAttention weiter, wenn die Sequenzlänge zwischen 4.096 und 131.072 variierte. Sie haben die Gesamtzeit von Vorwärts- und Vorwärts- und Rückwärtsvorgängen gemessen, wenn sie mit FlashAttention berechnet oder mit HyperAttention beschleunigt wurden. Es wurde auch die Uhrzeit der Wanduhr mit und ohne Kausalmaskierung gemessen. Alle Eingaben Q, K und V haben die gleiche Länge, die Dimensionalität ist auf d = 64 festgelegt und die Anzahl der Aufmerksamkeitsköpfe beträgt 12.
Sie wählen die gleichen Parameter wie zuvor in HyperAttention. Wie in Abbildung 4 dargestellt, erhöht sich die Geschwindigkeit von HyperAttention um das 54-fache, wenn die Kausalmaske nicht angewendet wird, und mit der Kausalmaske wird die Geschwindigkeit um das 5,4-fache erhöht. Obwohl die zeitliche Verwirrung von Kausalmaskierung und Nichtmaskierung gleich ist, erfordert der eigentliche Algorithmus der Kausalmaskierung (Algorithmus 1) zusätzliche Operationen wie die Partitionierung von Q, K und V und die Zusammenführung von Aufmerksamkeitsausgaben, was zu einer Erhöhung der tatsächlichen Laufzeit führt. Wenn die Sequenzlänge n zunimmt, wird die Beschleunigung höher sein
Die Forscher glauben, dass diese Ergebnisse nicht nur auf Schlussfolgerungen anwendbar sind, sondern auch zum Trainieren oder Feinabstimmen von LLM verwendet werden können, um sich an längere Sequenzen anzupassen, was neue Möglichkeiten eröffnet die Erweiterung der Selbstaufmerksamkeit Neue Möglichkeiten

Das obige ist der detaillierte Inhalt vonNeuer ungefährer Aufmerksamkeitsmechanismus HyperAttention: freundlich zu langen Kontexten, beschleunigt die LLM-Inferenz um 50 %. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Was ist ein Haufen? Was ist der Methodenbereich? Einführung in den Heap- und Methodenbereich im JVM-Speichermodell
- Was ist das CSS-Box-Modell?
- Was sind die vier gängigen Softwareentwicklungsmodelle?
- So kopieren Sie ein Modell in eine andere Datei in 3dmax
- Programmierer sind in Gefahr! Es heißt, dass OpenAI weltweit Outsourcing-Truppen rekrutiert und ChatGPT-Code-Farmer Schritt für Schritt schult

