GPT-4 erstellt ein „Weltmodell', das es LLM ermöglicht, aus „falschen Fragen' zu lernen und seine Denkfähigkeit erheblich zu verbessern

In jüngster Zeit haben große Sprachmodelle bedeutende Durchbrüche bei verschiedenen Aufgaben der Verarbeitung natürlicher Sprache erzielt, insbesondere bei mathematischen Problemen, die eine komplexe Gedankenkette (CoT) erfordern.

Zum Beispiel in GSM8K, MATH usw. Proprietäre Modelle einschließlich GPT -4 und PaLM-2 haben bemerkenswerte Ergebnisse bei Datensätzen schwieriger mathematischer Aufgaben erzielt. In dieser Hinsicht besteht bei Open-Source-Großmodellen noch erheblicher Verbesserungsbedarf. Um die CoT-Inferenzfähigkeiten großer Open-Source-Modelle für mathematische Aufgaben weiter zu verbessern, besteht ein gängiger Ansatz darin, diese Modelle mithilfe annotierter/generierter Frage-Inferenz-Datenpaare (CoT-Daten) zu verfeinern, die dem Modell direkt beibringen, wie es Aufgaben auf diesen ausführt Führen Sie während der Aufgabe eine CoT-Inferenz durch.

Kürzlich diskutierten Forscher der Xi'an Jiaotong University, der Microsoft und der Peking University in einem Papier eine Verbesserungsidee, die darin besteht, die Denkfähigkeit durch den Reverse-Learning-Prozess (d. h. Lernen aus den Fehlern des LLM) weiter zu verbessern.

Genau wie ein Schüler, der mit dem Mathematiklernen beginnt, wird er zunächst sein Verständnis verbessern, indem er die Wissenspunkte und Beispiele im Lehrbuch studiert. Gleichzeitig macht er aber auch Übungen, um das Gelernte zu festigen. Wenn er auf Schwierigkeiten stößt oder bei der Lösung eines Problems scheitert, erkennt er, welche Fehler er gemacht hat, und lernt, diese zu korrigieren, und erstellt so ein „Fehlerbuch“. Durch das Lernen aus Fehlern werden seine Denkfähigkeiten weiter verbessert

Inspiriert durch diesen Prozess untersucht diese Arbeit, wie die Denkfähigkeiten eines LLM vom Verstehen und Korrigieren von Fehlern profitieren.

Papieradresse: https://arxiv.org/pdf/2310.20689.pdf

Konkret generierten die Forscher zunächst Fehlerkorrektur-Datenpaare (sogenannte Korrekturdaten) und verwendeten dann Korrekturdaten, um Feinabstimmung von LLM. Bei der Generierung von Korrekturdaten: Was neu geschrieben werden musste, verwendeten sie mehrere LLMs (einschließlich LLaMA und der GPT-Modellfamilie), um ungenaue Inferenzpfade zu sammeln (d. h. die endgültige Antwort war falsch) und verwendeten anschließend GPT-4 als „ „Korrektor „Um Korrekturen für diese ungenauen Argumentationspfade zu generieren

Die generierten Korrekturen enthalten drei Informationen: (1) den falschen Schritt in der ursprünglichen Lösung; (2) eine Erklärung, warum der Schritt falsch war; (3) wie richtig die ursprüngliche Lösung, um zur richtigen Endantwort zu gelangen. Nach dem Herausfiltern von Korrekturen mit falschen Endantworten ergab die manuelle Auswertung, dass die Korrekturdaten eine ausreichende Qualität für die anschließende Feinabstimmungsphase aufwiesen. Die Forscher verwendeten QLoRA zur Feinabstimmung des LLM anhand von CoT-Daten und Korrekturdaten und führten so das „Lernen aus Fehlern“ (LEMA) durch.

Untersuchungen zeigen, dass das aktuelle LLM einen schrittweisen Ansatz zur Lösung von Problemen verwenden kann. Dieser mehrstufige Generierungsprozess bedeutet jedoch nicht, dass das LLM selbst über starke Argumentationsfähigkeiten verfügt. Dies liegt daran, dass sie möglicherweise nur das oberflächliche Verhalten des menschlichen Denkens nachahmen, ohne die zugrunde liegende Logik und die erforderlichen Regeln wirklich zu verstehen.

Dieser Mangel an Verständnis führt zu Fehlern im Denkprozess, sodass die Hilfe eines „Weltmodells“ erforderlich ist . Weil das „Weltmodell“ von vornherein ein Bewusstsein für die Logik und die Regeln der realen Welt hat. Aus dieser Perspektive kann das LEMA-Framework in diesem Artikel so gesehen werden, dass es GPT-4 als „Weltmodell“ verwendet, um kleineren Modellen beizubringen, diesen Logiken und Regeln zu folgen, anstatt nur Schritt-für-Schritt-Verhalten zu imitieren.

Lassen Sie uns nun einen Blick auf die spezifischen Implementierungsschritte dieser Studie werfen korrigierte Daten: Erforderlich. Es gibt zwei Hauptphasen: Neuschreiben des Inhalts und Feinabstimmung des LLM. Abbildung 1 (rechts) zeigt die Leistung von LEMA bei GSM8K- und MATH-Datensätzen

Korrigierte Daten generieren: Was muss neu geschrieben werden

Anhand eines Frage- und Antwortbeispiels 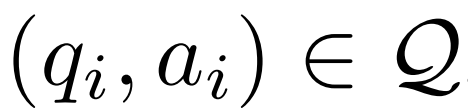, eines Korrekturmodells M_c und eines Inferenzmodells M_r generierte der Forscher Fehlerkorrekturdatenpaare 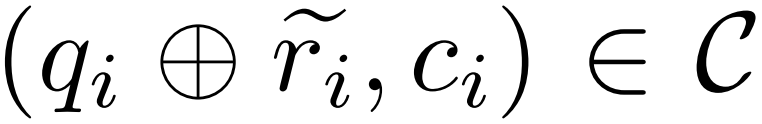, wobei 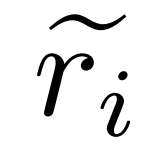den ungenauen Inferenzpfad der Frage q_i und c_i das Paar darstellt Korrektur von .

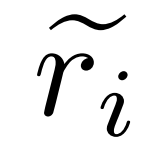Korrektur eines ungenauen Argumentationspfades . Der Forscher verwendet zunächst das Inferenzmodell M_r, um mehrere Inferenzpfade für jede Frage q_i abzutasten, und behält dann nur die Pfade bei, die letztendlich nicht zur richtigen Antwort a_i führen, wie in der folgenden Formel (1) dargestellt.

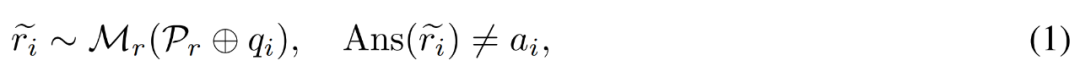
Generieren Sie Korrekturen für Fehler. Für die Frage q_i und den ungenauen Argumentationspfad 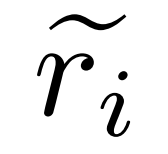verwendet der Forscher das Korrekturmodell M_c, um eine Korrektur zu generieren, und überprüft dann die richtige Antwort in der Korrektur, wie in Gleichung (2) unten dargestellt.

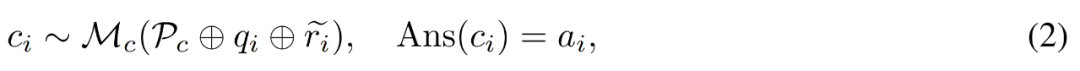
P_c enthält hier vier annotierte Fehlerkorrekturbeispiele, um dem Korrekturmodell Orientierung zu geben, welche Art von Informationen in die generierten Korrekturen einbezogen werden sollen

Konkret umfassen die annotierten Korrekturen die folgenden drei Arten von Informationen:

• Fehlerschritt: Welcher Schritt im ursprünglichen Argumentationspfad ist schief gelaufen.
• Erklärung: Welche Art von Fehler ist in diesem Schritt aufgetreten?
• Richtige Lösung: So beheben Sie den ungenauen Argumentationspfad, um das ursprüngliche Problem besser zu lösen.

Bitte sehen Sie sich das Bild unten an. Abbildung 1 zeigt kurz die Eingabeaufforderungen, die zum Generieren von Korrekturen verwendet werden. Bevor wir größere Daten generieren, haben wir zunächst manuell die Qualität der generierten Korrekturen bewertet. Sie verwendeten LLaMA-2-70B als M_r und GPT-4 als M_c und generierten 50 fehlerkorrigierte Datenpaare basierend auf dem GSM8K-Trainingssatz.

Forscher klassifizierten Korrekturen in drei Qualitätsstufen: ausgezeichnet, gut und schlecht. Hier ist ein Beispiel für drei Stufen

Die Bewertungsergebnisse ergaben, dass 35 von 50 Build-Korrekturen eine ausgezeichnete Qualität erreichten, 11 waren gut und 4 waren schlecht. Basierend auf dieser Auswertung kamen die Forscher zu dem Schluss, dass die Gesamtqualität der mit GPT-4 generierten Korrekturen für weitere Feinabstimmungsschritte ausreichend war. Daher generierten sie umfangreichere Korrekturen und verwendeten alle Korrekturen, die letztendlich zur richtigen Antwort auf das LLM führten, die einer Feinabstimmung bedurfte.

Es ist das LLM, das einer Feinabstimmung bedarf

Nach der Generierung von Korrekturdaten: Was musste neu geschrieben werden, optimierten die Forscher das LLM, um zu bewerten, ob die Modelle aus ihren Fehlern lernen konnten. Sie führen hauptsächlich Leistungsvergleiche unter den folgenden zwei Feinabstimmungseinstellungen durch.

Die erste besteht in der Feinabstimmung der Chain of Thought (CoT)-Daten. Forscher verfeinern das Modell nur anhand von Daten zur Fragebegründung. Obwohl jede Aufgabe kommentierte Daten enthält, nutzen sie zusätzlich die CoT-Datenerweiterung. Die Forscher verwendeten GPT-4, um mehr Argumentationspfade für jede Frage im Trainingssatz zu generieren und Pfade mit falschen Endantworten herauszufiltern. Sie nutzen die Erweiterung der CoT-Daten, um eine robuste Basis für die Feinabstimmung zu erstellen, die nur CoT-Daten verwendet und Ablationsstudien über die Datengröße erleichtert, die die Feinabstimmung steuert.

Das zweite ist die Feinabstimmung der CoT-Daten + korrigierten Daten. Zusätzlich zu den CoT-Daten generierten die Forscher auch Fehlerkorrekturdaten zur Feinabstimmung (d. h. LEMA). Sie führten außerdem Ablationsexperimente mit kontrollierter Datengröße durch, um die Auswirkungen von Inkrementen auf die Datengröße zu reduzieren.

Beispiel 5 und Beispiel 6 in Anhang A zeigen das Eingabe-Ausgabe-Format von CoT-Daten bzw. Korrekturdaten zur Feinabstimmung LEMA bei fünf Open-Source-LLMs und zwei anspruchsvollen Aufgaben zum mathematischen Denken. Beispielsweise erzielte LEMA mit LLaMA-2-70B Ergebnisse von 83,5 % bzw. 25,0 % bei GSM8K und MATH, während die Feinabstimmung nur bei CoT-Daten Ergebnisse von 81,4 % bzw. 23,6 % erzielte , LEMA ist mit proprietärem LLM kompatibel: LEMA mit WizardMath-70B/MetaMath-70B erreicht 84,2 %/85,4 % Pass@1-Genauigkeit auf GSM8K und 27,1 %/26,9 % auf MATH. Die Pass@1-Genauigkeitsrate übertrifft die von vielen erreichte SOTA-Leistung Open-Source-Modelle für diese anspruchsvollen Aufgaben.

Nachfolgende Ablationsstudien zeigen, dass LEMA bei gleicher Datenmenge immer noch die CoT-Feinabstimmung allein übertrifft. Dies deutet darauf hin, dass CoT-Daten und korrigierte Daten nicht gleichermaßen effektiv sind, da die Kombination beider Datenquellen eine größere Verbesserung bringt als die Verwendung einer einzelnen Datenquelle. Diese experimentellen Ergebnisse und Analysen verdeutlichen das Potenzial des Lernens aus Fehlern zur Verbesserung der LLM-Inferenzfähigkeiten.

Weitere Forschungsdetails finden Sie im Originalpapier

Das obige ist der detaillierte Inhalt vonGPT-4 erstellt ein „Weltmodell', das es LLM ermöglicht, aus „falschen Fragen' zu lernen und seine Denkfähigkeit erheblich zu verbessern. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!