Heim >Technologie-Peripheriegeräte >KI >Tao Zhexuan beginnt mit Copilot: Unglaublich, es kann anhand des Theoremnamens die Richtung erraten, die ich möchte
Tao Zhexuan beginnt mit Copilot: Unglaublich, es kann anhand des Theoremnamens die Richtung erraten, die ich möchte
- PHPznach vorne
- 2023-10-23 20:13:09584Durchsuche
Nachdem er GPT-4 ausprobiert hatte, nutzte Tao Zhexuan erneut Github Copilot.
Dieses Mal besteht sein Versuchsszenario darin, die Lean-Sprache zu lernen und sie zur Formalisierung mathematischer Theoreme zu verwenden.

Bei großen Modellen ist auch der formale Theorembeweis eine Herausforderung. Ein formaler Beweis ist im Wesentlichen ein Computerprogramm, aber im Gegensatz zu herkömmlichen Programmen in C++ oder Python kann die Korrektheit des Beweises mithilfe von Beweisassistenten wie der Lean-Sprache überprüft werden. Das Beweisen von Theoremen ist eine spezielle Form der Codegenerierung, die in ihrer Bewertung sehr streng ist und keinen Raum für Illusionen im Modell lässt.
Der von Terence Tao erwähnte Satz stammt aus einem Aufsatz vom 9. Oktober:

Der Beweis im Aufsatz umfasst weniger als eine Seite, aber Terence Taos formaler Beweis verwendet 200 Zeilen Lean-Sprache.
Zum Beispiel behauptet Terence Tao in der Arbeit nur, dass für jedes a>0  in reellen Zahlen konvex ist, da dies eine reguläre Rechenübung ist, und nennt dann Jensens Ungleichung, schreibt aber alle Details auf. Es dauerte etwa 50 Codezeilen.
in reellen Zahlen konvex ist, da dies eine reguläre Rechenübung ist, und nennt dann Jensens Ungleichung, schreibt aber alle Details auf. Es dauerte etwa 50 Codezeilen.
Tao Zhexuan sagte, dass die Fähigkeit des Github-Copiloten, mehrere Codezeilen für verschiedene Routineüberprüfungen korrekt vorherzusagen und aus Hinweisen wie den Namen von Theoremen die gewünschte Richtung abzuleiten, „unglaublich“ sei.
Leans Strategie „Umschreiben“ ist unverzichtbar und ermöglicht es Ihnen, lange Annahmen oder Ziele durch gezielte Ersetzungen zu ändern, die auf den Ausdruck einwirken, ohne ihn vollständig eingeben zu müssen.
„Wenn ich Beweise in LaTeX schreibe, simuliere ich diese Methode oft grob, indem ich den langen Ausdruck, mit dem ich es zu tun habe, von einer Zeile zur nächsten ausschneide und einfüge und dann gezielte Änderungen vornehme, aber das führt manchmal zu Tippfehlern. Er ist über mehrere verteilt.“ Zeilen im Dokument, daher ist es gut, es automatisch und überprüfbar umschreiben zu können
Tao Zhexuan sagte, dass das nächste Ziel darin besteht, eine einfache Version dieser Ungleichung zu etablieren, nämlich die Ungleichung (1,8) in der Arbeit: 
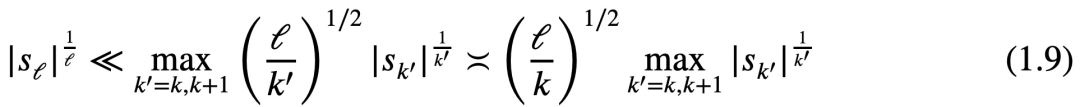

Das obige ist der detaillierte Inhalt vonTao Zhexuan beginnt mit Copilot: Unglaublich, es kann anhand des Theoremnamens die Richtung erraten, die ich möchte. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

