Heim >Technologie-Peripheriegeräte >KI >Einblick in die Matrixmultiplikation aus 3D-Perspektive, so sieht KI-Denken aus
Einblick in die Matrixmultiplikation aus 3D-Perspektive, so sieht KI-Denken aus
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-10-16 08:09:011100Durchsuche
Wenn der Ausführungsprozess der Matrixmultiplikation in 3D dargestellt werden kann, wird es damals nicht so schwierig sein, die Matrixmultiplikation zu erlernen.
Heutzutage ist die Matrixmultiplikation zum Baustein maschineller Lernmodelle und zur Grundlage verschiedener leistungsstarker KI-Technologien geworden. Das Verständnis ihrer Ausführungsmethode wird uns definitiv helfen, diese KI und diese zunehmend intelligente Welt besser zu verstehen.
In diesem Artikel aus dem PyTorch-Blog wird mm vorgestellt, ein Visualisierungstool für die Matrixmultiplikation und Matrixmultiplikationskombination.
Da mm im Vergleich zu herkömmlichen zweidimensionalen Diagrammen alle drei räumlichen Dimensionen nutzt, hilft mm dabei, Ideen intuitiv darzustellen und anzuregen, und erfordert weniger kognitiven Aufwand, insbesondere (aber nicht beschränkt auf) für Menschen, die gut im visuellen und räumlichen Bereich sind Denken.
Und mit drei Dimensionen zum Kombinieren von Matrixmultiplikationen sowie der Möglichkeit, trainierte Gewichte zu laden, kann mm große zusammengesetzte Ausdrücke (z. B. Aufmerksamkeitsköpfe) visualisieren und ihre tatsächlichen Verhaltensmuster beobachten.
mm ist vollständig interaktiv, läuft in einem Browser- oder Notebook-Iframe und speichert den vollständigen Status in der URL, sodass der Link eine gemeinsam nutzbare Sitzung ist (die Screenshots und Videos in diesem Artikel verfügen über einen Link, verfügbar unter Öffnen Sie die entsprechende Visualisierung Weitere Informationen zu diesem Tool finden Sie im Originalblog. In diesem Referenzhandbuch werden alle verfügbaren Funktionen beschrieben.
Tool-Adresse: https://bhosmer.github.io/mm/ref.html
Original-Blogtext: https://pytorch.org/blog/inside-the-matrix
Dies Der Artikel ist der erste, in dem ich Visualisierungsmethoden vorstelle, durch die Visualisierung einiger einfacher Matrixmultiplikationen und Ausdrücke eine Intuition aufbaue und mich dann mit einigen erweiterten Beispielen befasse:
Einführung: Warum ist diese Visualisierung besser?
Warm-up: Animation – Sehen Sie, wie die kanonische Matrixmultiplikationszerlegung funktioniert
Warm-up: Ausdrücke – Ein kurzer Blick auf einige grundlegende Ausdrucksbausteine
Tief in den Aufmerksamkeitskopf: Tiefer Blick mit NanoGPT Struktur, Werte und Rechenverhalten eines Paares von Aufmerksamkeitsköpfen für GPT-2
Aufmerksamkeit parallelisieren: Visualisieren Sie die Parallelisierung von Aufmerksamkeitsköpfen anhand von Beispielen aus dem aktuellen Blockwise Parallel Transformer-Artikel.
Größe der Aufmerksamkeitsschicht: Wenn wir uns die gesamte Aufmerksamkeitsschicht als eine einzige Struktur vorstellen, wie sehen dann die MHA-Hälfte und die FFA-Hälfte der Aufmerksamkeitsschicht zusammen aus? Wie verändert sich das Bild während des autoregressiven Decodierungsprozesses?
LoRA: Eine detaillierte visuelle Erklärung dieser Aufmerksamkeitskopfarchitektur
1 Einführung
mms Visualisierungsansatz basiert auf der Prämisse, dass die Matrixmultiplikation im Wesentlichen eine dreidimensionale Operation ist.
Mit anderen Worten:
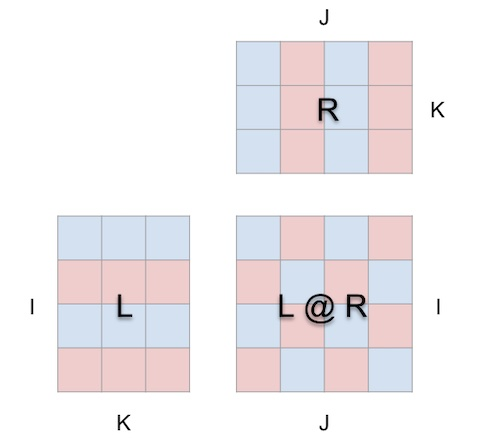
kann man sich tatsächlich so vorstellen:

Wenn wir die Matrixmultiplikation auf diese Weise in einen Würfel packen, bestehen zwischen der Parameterform, der Ergebnisform und der gemeinsamen Dimension die richtigen Beziehungen sind alle vorhanden.
Jetzt macht die Matrixmultiplikationsberechnung geometrisch Sinn: Jede Position i, j in der resultierenden Matrix verankert einen Vektor, der entlang der Tiefendimension k im Inneren des Würfels verläuft und sich von der i-ten Reihe von L aus erstreckt. Die horizontale Ebene schneidet die Vertikale Ebene, die von der j-ten Spalte von R ausgeht. Entlang dieses Vektors treffen Paare von (i, k) (k, j)-Elementen aus den linken und rechten Argumenten aufeinander und werden multipliziert. Die resultierenden Produkte werden entlang k summiert und an der Position i des Ergebnisses, j, platziert.
Dies ist die intuitive Bedeutung der Matrixmultiplikation:
1. Projizieren Sie zwei orthogonale Matrizen in das Innere eines Würfels.
2. Summieren Sie entlang der dritten orthogonalen Dimension, um die resultierende Matrix zu erstellen.
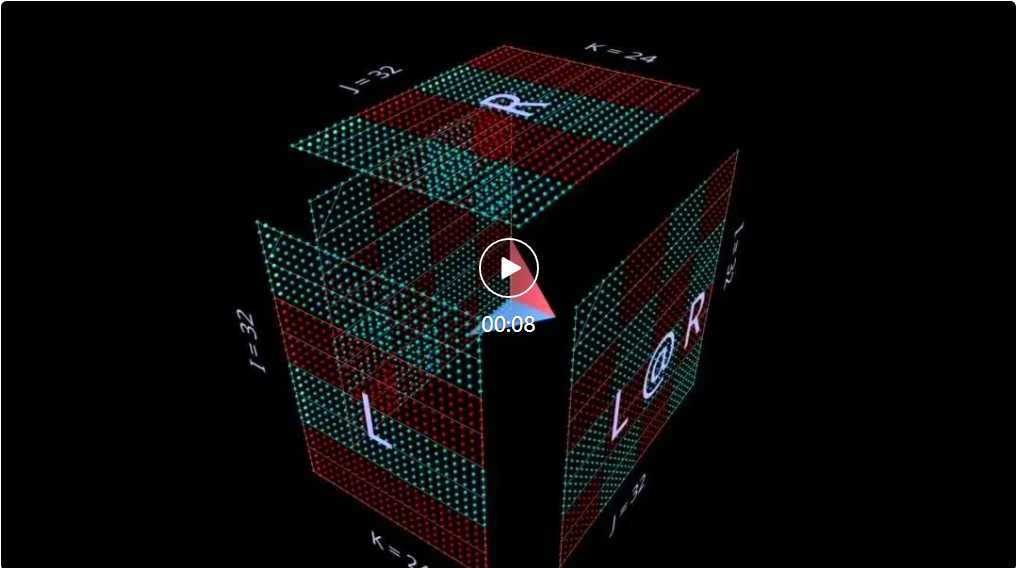
Für die Richtung zeigt das Werkzeug einen Pfeil im Würfel an, der auf die Ergebnismatrix zeigt, wobei der linke Parameter blau und der rechte Parameter rot ist. Das Tool zeigt außerdem weiße Indikatorlinien an, um die Zeilenachse jeder Matrix anzuzeigen, obwohl diese Linien in diesem Screenshot verschwommen sind.
Die Layoutbeschränkungen sind einfach und unkompliziert:
- Die Parameter und Ergebnisse auf der linken Seite müssen entlang ihrer gemeinsamen Höhendimension (i) benachbart sein.
- Die Parameter und Ergebnisse auf der rechten Seite müssen entlang ihrer gemeinsamen Breite benachbart sein (j) Dimension
- Die linken und rechten Parameter müssen entlang ihrer gemeinsamen Dimension (linke Breite / rechte Höhe) benachbart sein, die zur Tiefendimension (k) der Matrixmultiplikation wird
- Diese geometrische Darstellung kann verwendet werden Zur Visualisierung aller Standard-Matrixmultiplikationen bietet die Faktorisierung eine solide Grundlage und eine intuitive Grundlage für die Erforschung nichttrivialer Kombinationen komplexer Matrixmultiplikationen, wie wir als Nächstes sehen werden.
Bevor wir uns mit komplexeren Beispielen befassen, schauen wir uns an, wie dieser Visualisierungsstil aussieht, um ein intuitives Verständnis des Tools zu entwickeln.
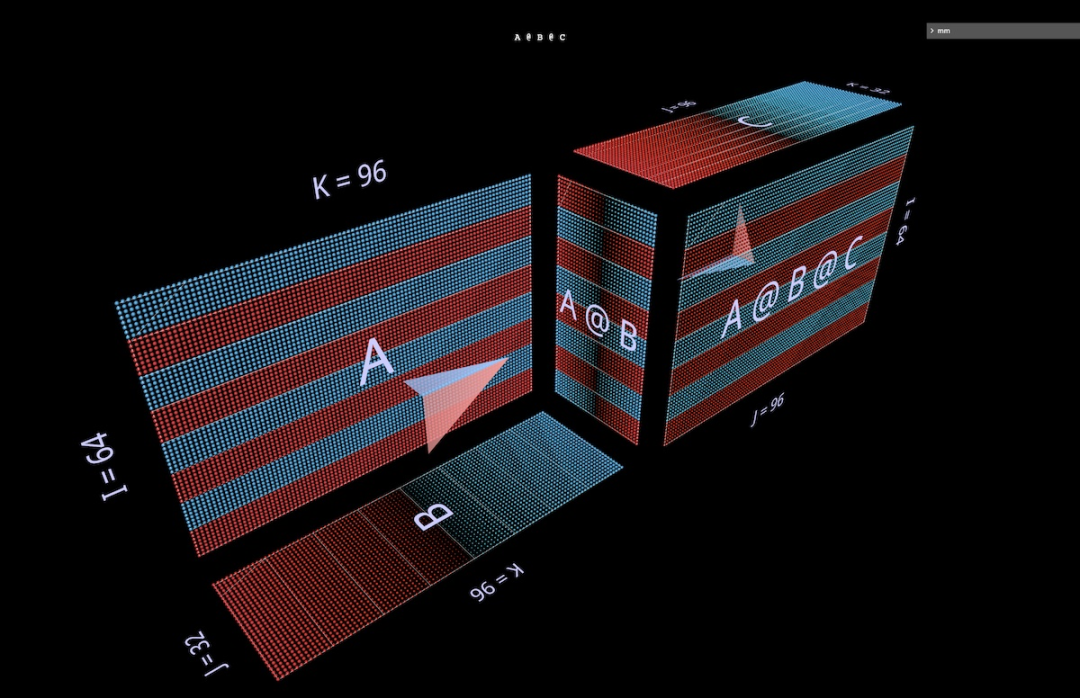
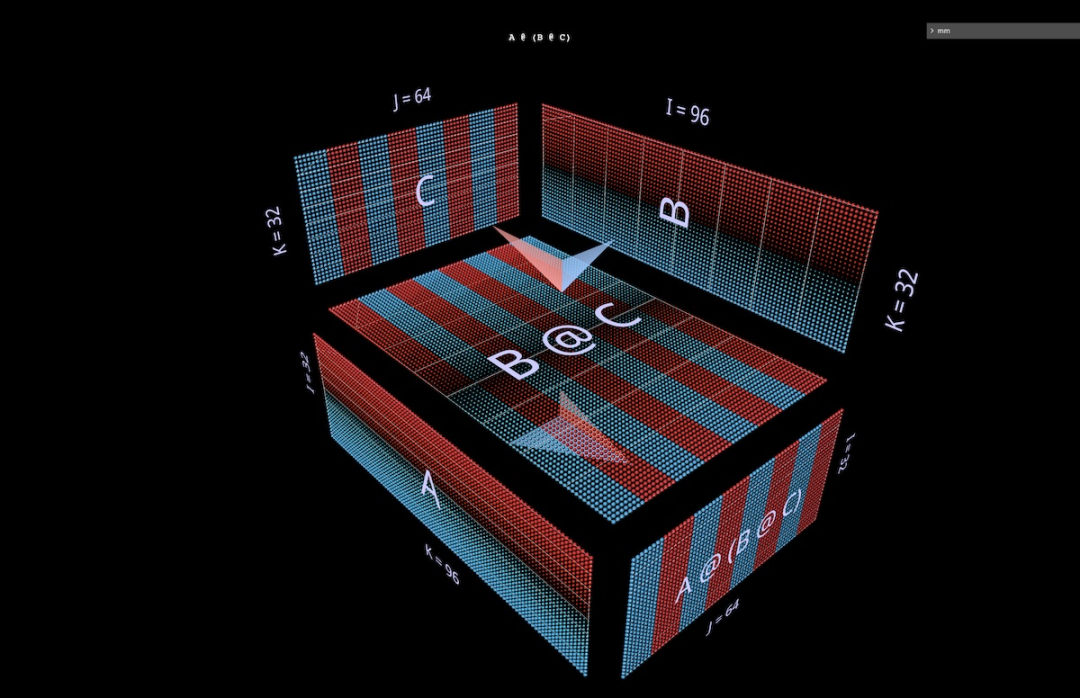
2ein PunktproduktSchauen wir uns zunächst einen klassischen Algorithmus an – berechnen Sie jedes Ergebniselement, indem Sie das Skalarprodukt der entsprechenden linken Zeile und rechten Spalte berechnen. Wie Sie in der Animation hier sehen können, durchläuft der Vektor mit multiplizierten Werten das Innere des Würfels und liefert jedes Mal ein summiertes Ergebnis an der entsprechenden Stelle. Hier hat L Blöcke mit Zeilen, die mit 1 (blau) oder -1 (rot) gefüllt sind; R hat Blöcke mit Spalten, die ähnlich gefüllt sind. Hier ist k 24, daher hat die resultierende Matrix (L @ R) einen Blauwert von 24 und einen Rotwert von -24. 2b Matrix-Vektor-Produkt zerlegt in Matrix-Vektor-Produkt. Die Matrixmultiplikation sieht aus wie eine vertikale Ebene (das Produkt jeder Spalte des linken Parameters und des rechten Parameters), die horizontal über das Innere von streicht Zeichnen Sie im Würfel die Spalten auf das Ergebnis: Es kann interessant sein, die Zwischenwerte einer Zerlegung zu beobachten, auch wenn das Beispiel einfach ist. Beachten Sie beispielsweise, dass das Matrix-Vektor-Produkt in der Mitte das vertikale Muster hervorhebt, wenn wir zufällig initialisierte Parameter verwenden – dies spiegelt die Tatsache wider, dass jeder Zwischenwert eine spaltenskalierte Kopie des Parameters auf der linken Seite ist: 2c Vektor – Matrixprodukt zerfällt in einen Vektor – Matrixmultiplikation von Matrixprodukten sieht aus wie eine horizontale Ebene, die Zeilen auf das Ergebnis zeichnet, während es im Inneren des Würfels entlangläuft: Umschalten Bei zufällig initialisierten Parametern können Sie ein Muster sehen, das dem Matrix-Vektor-Produkt ähnelt – nur dieses Mal im horizontalen Modus, was der Tatsache entspricht, dass jedes dazwischenliegende Vektor-Matrix-Produkt eine zeilenskalierte Kopie des rechten Parameters ist. Wenn man darüber nachdenkt, wie die Matrixmultiplikation die Rang-Summen-Struktur ihrer Parameter darstellt, besteht ein nützlicher Ansatz darin, sich vorzustellen, dass diese beiden Modi gleichzeitig in der Berechnung auftreten: 2d Summieren der externen Produkte Die Zerlegung der dritten Ebene erfolgt entlang der k-Achse. Die Ergebnisse der Matrixmultiplikation werden durch punktweise Summierung der äußeren Vektorprodukte berechnet. Hier können wir sehen, dass die äußere Produktebene den Würfel „von hinten nach vorne“ durchläuft und sich zu dem Ergebnis summiert: Unter Verwendung einer zufällig initialisierten Matrix für diese Zerlegung können wir nicht nur die Werte, sondern auch die Ergebnisse sehen Die Ränge von werden akkumuliert, wenn jedes äußere Produkt von Rang 1 dazu addiert wird. Dies erklärt auch intuitiv, warum die „Faktorisierung mit niedrigem Rang“ (d. h. die Approximation einer Matrix durch die Konstruktion einer Matrixmultiplikation mit kleineren Parametern in der Tiefendimension) am besten funktioniert, wenn die Matrix, die angenähert wird, eine Matrix mit niedrigem Rang ist. Dies ist LoRA, das später erwähnt wird: 3 Aufwärmen: Ausdrücke Auf welche Weise können wir diese Visualisierungsmethode auf die Zerlegung von Matrixmultiplikationen erweitern? Das vorherige Beispiel visualisierte eine einzelne Matrixmultiplikation L @ R der Matrizen L und R, aber was wäre, wenn L und/oder R selbst Matrixmultiplikationen wären? Es stellt sich heraus, dass sich dieser Ansatz gut für zusammengesetzte Ausdrücke eignet. Die Schlüsselregel ist einfach: Die Unterausdrucks-(Unter-)Matrixmultiplikation ist ein weiterer Würfel, der denselben Layoutbeschränkungen unterliegt wie die übergeordnete Matrixmultiplikation. Die Ergebnisfläche der Untermatrixmultiplikation ist ebenso wie eine kovalente Fläche die Parameterfläche der übergeordneten Matrixmultiplikation Geteilte Elektronen. Innerhalb dieser Einschränkungen können wir verschiedene Aspekte der Submatrix-Multiplikation entsprechend unseren eigenen Bedürfnissen arrangieren. Hier wird das Standardschema des Werkzeugs verwendet, das abwechselnd konvexe und konkave Würfel erzeugt. Dieses Layout funktioniert in der Praxis gut, da es den Platz maximiert und gleichzeitig die Okklusion minimiert. (Das Layout ist jedoch vollständig anpassbar. Weitere Informationen finden Sie auf der Seite mit den MM-Tools.) In diesem Abschnitt werden einige der wichtigsten Bausteine von Modellen für maschinelles Lernen visualisiert, damit sich die Leser mit dieser visuellen Darstellung vertraut machen und daraus neue Erkenntnisse gewinnen können. 3a Linke assoziative Ausdrücke Im Folgenden werden zwei Ausdrücke der Form (A @ B) @ C vorgestellt, jeder mit seiner eigenen einzigartigen Form und seinen eigenen Eigenschaften. (Hinweis: mm folgt der Konvention, dass die Matrixmultiplikation linksassoziativ ist, sodass (A @ B) @ C einfach als A @ B @ C geschrieben werden kann.) Geben Sie A @ B @ C zunächst eine sehr charakteristische FFN-Form, wobei Die „versteckte Dimension“ ist breiter als die „Eingabe“- oder „Ausgabe“-Dimension. (In diesem Beispiel bedeutet dies insbesondere, dass die Breite von B größer ist als die Breite von A oder C.) Wie beim Beispiel der Einzelmatrixmultiplikation zeigt der schwebende Pfeil auf die resultierende Matrix, von der die blaue Befiederung stammt Im linken Argument kommt die rote Befiederung von den Parametern auf der rechten Seite. Und wenn die Breite von B kleiner ist als die Breite von A oder C, entsteht ein Engpass bei der Visualisierung von A @ B @ C, ähnlich der Form eines Autoencoders. Das Muster alternierender Bump-Module kann auch auf Ketten beliebiger Länge erweitert werden: Zum Beispiel dieser mehrschichtige Engpass: 3b Rechter assoziativer Ausdruck Als nächstes visualisieren Sie den rechten assoziativen Ausdruck A @ ( B @ C). Ähnlich wie die horizontale Erweiterung eines linken assoziativen Ausdrucks – man kann sagen, dass sie vom linken Parameter des Wurzelausdrucks ausgeht, wird die Kette des rechten assoziativen Ausdrucks vertikal erweitert, beginnend vom rechten Parameter des Wurzelausdrucks. Manchmal sieht man ein MLP in einer Rechtskombinationsform, bei der die rechte Seite die spaltenförmige Eingabe ist und die Gewichtsschicht von rechts nach links verläuft. Unter Verwendung der oben dargestellten Matrix des zweischichtigen FFN-Beispiels (nach entsprechender Transposition) würde es so aussehen: C ist jetzt die Eingabe, B ist die erste Schicht und A ist die zweite Schicht: Außerdem Abgesehen von der Befiederungsfarbe (links blau, rechts rot) ist der zweite visuelle Hinweis zur Unterscheidung der linken und rechten Parameter ihre Ausrichtung: Die Parameterreihen auf der linken Seite sind koplanar mit den Ergebnisreihen – sie liegen entlang die gleiche Achse (i) gestapelt. Zum Beispiel (B @ C) oben können uns beide Hinweise sagen, dass B der linke Parameter ist. 3c Binäre Ausdrücke Damit Visualisierungswerkzeuge nützlich sind, müssen sie nicht nur für einfache Lehrbeispiele, sondern auch für komplexere Ausdrücke problemlos verwendet werden können. In realen Anwendungsfällen ist ein binärer Ausdruck eine wichtige Strukturkomponente – eine Matrixmultiplikation mit Unterausdrücken auf der linken und rechten Seite. Hier sehen Sie den einfachsten Ausdruck der Form (A @ B) @ (C @ D): 3d Eine kleine Anmerkung: Partitionierung und Parallelität Eine vollständige Ausarbeitung dieses Themas geht über das hinaus ist der Umfang dieses Artikels, aber wir werden seinen praktischen Nutzen später im Abschnitt „Aufmerksamkeit“ sehen. Aber zum Aufwärmen schauen Sie sich zwei einfache Beispiele an, um zu sehen, wie dieser Visualisierungsstil das Denken über parallelisierte zusammengesetzte Ausdrücke sehr intuitiv machen kann – allein durch einfache geometrische Partitionierung. Das erste Beispiel besteht darin, die typische „datenparallele“ Partitionierung auf das obige Beispiel für einen mehrschichtigen Engpass mit Linksverknüpfung anzuwenden. Wir partitionieren entlang i und segmentieren den anfänglichen linken Parameter (den „Stapel“) und alle Zwischenergebnisse (die „Aktivierung“), nicht jedoch die nachfolgenden Parameter (die „Gewichte“) – diese Geometrie macht den Ausdruck Es wird offensichtlich, welcher Akteure werden segmentiert und bleiben intakt: Das zweite Beispiel ist ohne klare geometrische Unterstützung intuitiv schwer zu verstehen: Es zeigt, wie man den linken Teilausdruck ausdrückt, indem man einen binären Ausdruck parallelisiert, indem man den Ausdruck partitioniert und den rechten Teilausdruck entlang des Ausdrucks partitioniert i-Achse und Partitionierung des übergeordneten Ausdrucks entlang der k-Achse: 4 Tieferer Aufmerksamkeitskopf Werfen wir nun einen Blick auf den Aufmerksamkeitskopf von GPT-2 – insbesondere auf die „gpt2“ (kleine) Konfiguration des 4. Kopfes der 5. Schicht von NanoGPT (Anzahl der Schichten = 12, Anzahl der Köpfe = 12, Anzahl der Einbettungen). = 768), unter Verwendung von Gewichten von OpenAI über HuggingFace. Eingabeaktivierungen werden aus einem Vorwärtsdurchlauf des OpenWebText-Trainingsbeispiels entnommen, das 256 Token enthält. An diesem speziellen Kopf gibt es nichts Besonderes. Er wurde hauptsächlich ausgewählt, weil er ein sehr häufiges Aufmerksamkeitsmuster berechnet und sich in der Mitte des Modells befindet, wo die Aktivierungen strukturiert sind und einige interessante Texturen aufweisen. 4a-Struktur Dieser vollständige Aufmerksamkeitskopf wird als einzelner zusammengesetzter Ausdruck visualisiert, der bei der Eingabe beginnt und mit der projizierten Ausgabe endet. (Hinweis: Um die Autarkie sicherzustellen, wird die Ausgangsprojektion für jeden Kopf wie hier für Megatron-LM beschrieben durchgeführt.) Diese Berechnung enthält sechs Matrixmultiplikationen: Eine kurze Beschreibung dessen, was hier gemacht wird: Die Flügel der Windmühle sind Matrixmultiplikationen 1, 2, 3 und 6: Der erstere Satz sind die inneren Projektionen der Eingaben zu Q, K und V; der letztere sind die äußeren Projektionen von attn @ V zurück zum Einbettungsmaß. Es gibt zwei Matrixmultiplikationen in der Mitte; die erste berechnet die Aufmerksamkeitswerte (der konvexe Würfel hinten) und verwendet sie dann, um das Ausgabetoken (der konkave Würfel vorne) basierend auf dem Wertevektor zu erhalten. Kausalität bedeutet, dass die Aufmerksamkeitswerte ein unteres Dreieck bilden. Aber es wäre für die Leser besser, dieses Tool selbst im Detail zu erkunden, anstatt sich nur Screenshots oder das Video unten anzusehen, um es detaillierter zu verstehen – sowohl seine Struktur als auch die tatsächlichen Werte, die durchfließen den Berechnungsprozess. 4b Berechnung des Summenwertes Hier ist die Animation des Berechnungsprozesses des Aufmerksamkeitskopfes. Konkret betrachten wir (d. h. die Matrixmultiplikationen 1, 4, 5 und 6 oben, wobei K_t und V vorberechnet sind), die als verschmolzene Kette von Vektor-Matrix-Produkten berechnet werden: Jedes Element geht durch Aufmerksamkeit vom Input zum Output in einem Schritt. Weitere Optionen für diese Animation werden später im Abschnitt zur Parallelisierung behandelt, aber schauen wir uns zunächst an, was uns die berechneten Werte sagen. Wir können viele interessante Dinge sehen: Bevor wir die Aufmerksamkeitsberechnung besprechen, können Sie sehen, wie erstaunlich die Form von Q und K_t mit niedrigem Rang ist. Wenn man die Q@K_t-Vektormatrix-Produktanimation vergrößert, sieht sie noch anschaulicher aus: Die große Anzahl der Kanäle (eingebettete Positionen) in Q und K scheint in der Sequenz mehr oder weniger konstant zu sein, was ein nützliches Aufmerksamkeitssignal darstellt kann nur durch einen kleinen Satz eingebetteter Treiber generiert werden. Das Verständnis und die Nutzung dieses Phänomens ist Teil des Transformatoreffizienzprojekts SysML ATOM. Am bekanntesten sind den Menschen vielleicht die starken, aber unvollkommenen Diagonalen, die in der Aufmerksamkeitsmatrix erscheinen. Dies ist ein häufiges Muster, das in vielen Aufmerksamkeitsköpfen dieses Modells (und vieler Transformers) auftaucht. Es kann lokale Aufmerksamkeit erzeugen: Der Werttoken in der kleinen Nachbarschaft unmittelbar vor der Position des Ausgabetokens bestimmt weitgehend das Inhaltsmuster des Ausgabetokens. Allerdings variieren die Größe dieser Nachbarschaft und der Einfluss einzelner Token darin stark – dies lässt sich am nicht-diagonalen Frost im Aufmerksamkeitsraster und auch an der Aufmerksamkeitsmatrix erkennen, die entlang der Sequenz attn [i ] @ V-Vektor – Das Wellenmuster in der Matrixproduktebene. Aber beachten Sie, dass die lokale Nachbarschaft nicht das Einzige ist, was es zu beachten gilt: Die Spalte ganz links im Aufmerksamkeitsraster (entsprechend dem ersten Token der Sequenz) ist vollständig mit Werten ungleich Null (aber schwankenden Werten) gefüllt, die Dies bedeutet, dass jedes Ausgabe-Token bis zu einem gewissen Grad vom ersten Wert-Token beeinflusst wird. Darüber hinaus gibt es eine ungenaue, aber erkennbare Schwankung in der Dominanz des Aufmerksamkeitswerts zwischen der Nachbarschaft des aktuellen Tokens und dem ursprünglichen Token. Die Periode dieser Oszillation variiert, aber im Allgemeinen beginnt sie kurz und wird dann länger, je weiter man sich in der Sequenz bewegt (ähnlicherweise hängt der kausale Zusammenhang mit der Anzahl der Kandidaten-Aufmerksamkeits-Tokens pro Zeile zusammen). Um zu verstehen, wie (attn @ V) gebildet wird, ist es wichtig, sich nicht nur auf die Aufmerksamkeit zu konzentrieren – V ist ebenso wichtig. Jeder Ausgabeterm ist ein gewichteter Durchschnitt des gesamten V-Vektors: Im Extremfall, in dem die Aufmerksamkeit eine perfekte Diagonale ist, ist attn @ V nur eine exakte Kopie von V . Hier sehen wir etwas Strukturierteres: sichtbare bandartige Strukturen, bei denen ein bestimmtes Token in einer zusammenhängenden Unterfolge von Aufmerksamkeitsreihen eine hohe Punktzahl erzielt, überlagert mit einer Matrix, die eindeutig V ähnelt, aber dickere Diagonalen aufweist. Es gibt eine gewisse vertikale Okklusion. (Randbemerkung: Laut mm-Referenzhandbuch wird durch langes Drücken oder Klicken bei gedrückter Strg-Taste der tatsächliche numerische Wert des visuellen Elements angezeigt.) Denken Sie daran, dass die Eingabe in diesen Aufmerksamkeitskopf eine Zwischendarstellung und nicht der ursprüngliche tokenisierte Text ist, da wir uns in der mittleren Ebene (Ebene 5) befinden. Die in der Eingabe sichtbaren Muster regen daher an sich zum Nachdenken an – insbesondere die starken vertikalen Linien sind bestimmte Einbettungspositionen, deren Werte über weite Strecken der Sequenz gleichmäßig eine hohe Amplitude aufweisen – manchmal sogar fast vollständig. Aber das Interessante ist, dass der erste Vektor in der Eingabesequenz eindeutig ist und nicht nur das Muster dieser Spalten mit hoher Amplitude durchbricht, sondern auch an fast jeder Position atypische Werte trägt (Randbemerkung: hier nicht visualisiert, aber dieses Muster erscheint wiederholt über mehrere Beispieleingaben hinweg). Hinweis: Bezüglich der letzten beiden Punkte ist es erwähnenswert, dass es sich hier um eine Berechnung anhand einer einzelnen Beispieleingabe handelt. In der Praxis hat sich herausgestellt, dass jeder Kopf ein charakteristisches Muster aufweist, das über einen ziemlich großen Satz von Stichproben konsistent (wenn auch nicht identisch) ausgedrückt wird. Wenn man sich jedoch eine Visualisierung ansieht, die Aktivierungen enthält, muss man bedenken, dass die vollständige Verteilung der Eingabe erfolgt kann auf subtile Weise die Ideen und Intuitionen beeinflussen, die es inspiriert. Abschließend wird noch einmal empfohlen, die Animation direkt zu erkunden! 4c Es gibt viele interessante Unterschiede im Aufmerksamkeitskopf Bevor wir fortfahren, hier eine weitere Demonstration, die zeigt, wie nützlich es ist, das Modell einfach zu studieren, um zu verstehen, wie es im Detail funktioniert. Dies ist ein weiterer Aufmerksamkeitsleiter von GPT-2. Sein Verhaltensmuster ist ganz anders als das von Level 5 Head 4 – wie man es erwarten würde, da es sich in einem ganz anderen Teil des Modells befindet. Dieser Kopf befindet sich auf der ersten Ebene: Kopf 2 der Ebene 0: Bemerkenswerte Punkte: Die Aufmerksamkeit dieses Kopfes ist sehr gleichmäßig verteilt. Dies hat zur Folge, dass der relativ ungewichtete Durchschnitt von V (oder das entsprechende kausale Präfix von V) an jede Zeile von attn@V geliefert wird, wie in der Animation gezeigt: Wenn wir uns im Dreieck der Aufmerksamkeitsbewertung nach unten bewegen, gilt attn[i] @ V Vektor – Matrixprodukt mit kleinen Schwankungen und nicht einfach eine verkleinerte, nach und nach sichtbare Kopie von V. attn @ V weist eine erstaunliche vertikale Gleichmäßigkeit auf – das gleiche Wertemuster bleibt in der gesamten Sequenz in großen darin eingebetteten Säulenbereichen bestehen. Man kann sich diese als Eigenschaften vorstellen, die jedem Token gemeinsam sind. Randbemerkung: Einerseits könnte man angesichts des Effekts einer sehr gleichmäßigen Aufmerksamkeitsverteilung erwarten, dass attn @ V eine gewisse Konsistenz aufweist. Aber jede Zeile besteht aus einer kausalen Teilfolge von V und nicht aus der gesamten Folge – warum sollte dies nicht zu weiteren Änderungen führen, wie einer fortschreitenden Verformung, wenn man sich in der Folge nach unten bewegt? Eine visuelle Untersuchung zeigt, dass V entlang seiner Länge nicht einheitlich ist, sodass die Antwort in einer subtileren Eigenschaft seiner Werteverteilung liegen muss. Schließlich sollte die Ausgabe dieses Kopfes nach der Außenprojektion in vertikaler Richtung gleichmäßiger sein. Wir können einen starken Eindruck gewinnen: Die meisten von diesem Aufmerksamkeitskopf übermittelten Informationen bestehen aus Attributen, die von jedem Token in der Sequenz geteilt werden. Die Zusammensetzung seiner Ausgabeprojektionsgewichte kann diese Intuition verstärken. Alles in allem kommen wir nicht umhin, uns zu wundern: Die extrem regelmäßigen, stark strukturierten Informationen, die dieser Aufmerksamkeitskopf produziert, könnten durch etwas... weniger aufwändige Computermittel gewonnen worden sein. Dies ist sicherlich kein unerforschtes Gebiet, aber die Klarheit und der Reichtum der Visualisierung von Rechensignalen können äußerst nützlich sein, um sowohl neue Ideen zu generieren als auch Überlegungen zu bestehenden anzustellen. 4d Zurück zur Einführung: Freie Invarianten Rückblickend muss man es wiederholen: Der Grund dafür, dass wir aufmerksamkeitsorientierte nicht-triviale Kompositionsoperationen visualisieren und intuitiv halten können, sind wichtige algebraische Eigenschaften wie Parameter usw B. eine Form eingeschränkt ist oder welche parallelen Achsen sich bei welchen Operationen schneiden), erfordern diese Eigenschaften kein zusätzliches Nachdenken: Sie ergeben sich direkt aus den geometrischen Eigenschaften des visuellen Objekts und nicht aus zusätzlichen Regeln, die man sich merken muss. Zum Beispiel ist in diesen Aufmerksamkeitskopf-Visualisierungen deutlich zu erkennen, dass: Q und attn @ V die gleiche Länge haben, K und V die gleiche Länge haben und die Längen dieser Paare voneinander unabhängig sind other; Q hat die gleiche Breite wie K, V hat die gleiche Breite wie attn @ V und die Breiten dieser Paare sind unabhängig voneinander. Diese Strukturen sind strukturell real, ein einfaches Ergebnis davon, wo sich die Strukturkomponenten in der Verbundstruktur befinden und wie sie ausgerichtet sind. Dieser Vorteil der „freien Natur“ ist besonders nützlich, wenn Variationen typischer Strukturen untersucht werden – ein offensichtliches Beispiel ist die Dekodierung einer einzeiligen Matrix mit hoher Aufmerksamkeit in jeweils einem autoregressiven Token: 5 Parallelität Achtung Die Animation des 4. Kopfes der 5 Ebenen oben visualisiert 4 der 6 Matrixmultiplikationen im Aufmerksamkeitskopf. Sie werden als Fusionskette von Vektor-Matrix-Produkten visualisiert, was eine geometrische Intuition bestätigt: Die gesamte linksverknüpfende Kette von der Eingabe bis zur Ausgabe ist entlang der gemeinsamen i-Achse geschichtet und kann parallelisiert werden. 5a Beispiel: Partitionierung entlang i Um die Berechnung in der Praxis zu parallelisieren, können wir die Eingabe entlang der i-Achse in Blöcke unterteilen. Wir können diese Aufteilung im Tool visualisieren, indem wir angeben, dass eine bestimmte Achse in eine bestimmte Anzahl von Blöcken unterteilt wird – in diesen Beispielen wird 8 verwendet, aber diese Zahl ist nichts Besonderes. Darüber hinaus zeigt diese Visualisierung deutlich, dass jede parallele Berechnung das vollständige wQ (für die innere Projektion), K_t und V (für die Aufmerksamkeit) und wO (für die äußere Projektion) erfordert, da die unpartitionierten Dimensionen dieser Matrizen an die partitionierten angrenzen Matrizen: 5b Beispiel: Duale Partitionierung Ein Beispiel für die Partitionierung entlang mehrerer Achsen wird hier ebenfalls gegeben. Zu diesem Zweck stellen wir hier eine aktuelle Innovation in diesem Bereich vor, nämlich den Block Parallel Transformer (BPT), der auf einigen Forschungsergebnissen wie Flash Attention basiert. Bitte lesen Sie den Artikel: https://arxiv.org/. pdf/2305.19370.pdf Zuallererst unterteilt BPT wie oben beschrieben entlang i – und erweitert diese horizontale Unterteilung der Sequenz tatsächlich auch bis zur anderen Hälfte der Aufmerksamkeitsschicht (FFN). (Eine Visualisierung davon wird später gezeigt.) Um dieses Kontextlängenproblem vollständig zu lösen, fügen Sie MHA eine zweite Partition hinzu – die Partition der Aufmerksamkeitsberechnung selbst (d. h. die Partition entlang der j-Achse von Q @ K_t). Zusammen unterteilen diese beiden Partitionen die Aufmerksamkeit in ein Blockgitter: Wie aus dieser Visualisierung deutlich wird: Diese doppelte Partitionierung löst effektiv das Kontextlängenproblem, da wir jetzt die Sequenzlänge jedes Vorkommens visuell unterteilen können in der Aufmerksamkeitsberechnung. Der „Bereich“ der zweiten Partition: Aus der geometrischen Struktur geht hervor, dass die Berechnung der inneren Projektion von K und V zusammen mit der Kerndoppelmatrixmultiplikation partitioniert werden kann. Beachten Sie ein subtiles Detail: Der visuelle Hinweis hier ist, dass wir auch die nachfolgende Matrixmultiplikation attn @ V entlang k parallelisieren und die Teilergebnisse im Split-k-Stil summieren können, wodurch die gesamte Doppelmatrixmultiplikation parallelisiert wird. Aber zeilenweiser Softmax in sdpa() fügt eine Anforderung hinzu: Für jede Zeile muss die gesamte Segmentierung normalisiert werden, bevor die entsprechende Zeile von attn@V berechnet wird, was zusätzliche zeilenweise Schritte hinzufügt. 6 Größe der Aufmerksamkeitsschicht Es ist bekannt, dass die erste Hälfte der Aufmerksamkeitsschicht (MHA) aufgrund ihrer quadratischen Komplexität einen hohen Rechenaufwand hat, aber auch die zweite Hälfte (FFN) hat ihre eigenen Bedürfnisse, Dies liegt an der Breite seiner verborgenen Dimension, die normalerweise viermal so groß ist wie die Breite der eingebetteten Dimension des Modells. Die Visualisierung der Biomasse einer vollständigen Aufmerksamkeitsschicht hilft dabei, ein intuitives Verständnis dafür zu entwickeln, wie die beiden Hälften der Schicht miteinander verglichen werden. 6a Visualisierung der kompletten Aufmerksamkeitsschicht Unten ist eine komplette Aufmerksamkeitsschicht, mit der ersten Hälfte (MHA) hinten und der zweiten Hälfte (FFN) vorne. Auch hier zeigt der Pfeil in die Richtung der Berechnung. Hinweis: Diese Visualisierung stellt keinen einzelnen Aufmerksamkeitskopf dar, sondern zeigt die ungeschnittenen Q/K/V-Gewichte und Projektionen rund um die zentrale Doppelmatrixmultiplikation. Natürlich stellt dies nicht den gesamten MHA-Vorgang getreu dar – aber das Ziel besteht hier darin, eine klarere Vorstellung von den relativen Matrixgrößen in den beiden Hälften der Schicht zu bekommen und nicht vom relativen Rechenaufwand, der von jeder Hälfte ausgeführt wird. (Außerdem verwenden die Gewichte hier Zufallswerte anstelle realer Gewichte.) Die hier verwendeten Abmessungen werden verkleinert, um sicherzustellen, dass der Browser sie (relativ) tragen kann, aber die Proportionen bleiben gleich (aus der kleinen Konfiguration von NanoGPT). ): Modelleinbettungsdimension = 192 (ursprünglich 768), FFN-Einbettungsdimension = 768 (ursprünglich 3072), Sequenzlänge = 256 (ursprünglich 1024), obwohl die Sequenzlänge keinen grundlegenden Einfluss auf das Modell hat. (Visuell erscheinen Änderungen in der Sequenzlänge als Änderungen in der Breite des Eingabeblatts, was zu Änderungen in der Größe des Aufmerksamkeitszentrums und der Höhe der nachgeschalteten vertikalen Ebene führt.) Blockweiser paralleler Transformator, hier ist ein Parallelisierungsschema, das BPT im Kontext der gesamten Aufmerksamkeitsschicht visualisiert (Überschriften wie oben weggelassen). Beachten Sie insbesondere, wie sich die Partitionierung entlang i (dem Sequenzblock) über die MHA- und FFN-Hälften erstreckt: 6c Partitionierung des FFN Diese Visualisierungsmethode schlägt eine zusätzliche Partition vor, die orthogonal zu der oben beschriebenen ist: Teilen Sie auf der FFN-Hälfte der Aufmerksamkeitsschicht die Doppelmatrixmultiplikation (attn_out @ FFN_1) @ FFN_2 auf, zuerst entlang j attn_out @ FFN_1 und führen Sie dann die anschließende Matrixmultiplikation durch zusammen mit k mit FFN_2. Durch diese Partitionierung werden die beiden FFN-Gewichtungsschichten aufgeteilt, um die Kapazitätsanforderungen für jede an der Berechnung beteiligte Komponente auf Kosten der endgültigen Summierung der Teilergebnisse zu reduzieren. So sieht diese Partitionierungsmethode aus, wenn sie auf eine nicht partitionierte Aufmerksamkeitsebene angewendet wird: So sieht sie aus, wenn sie auf eine BPT-partitionierte Ebene angewendet wird: 6d-Visualisierung, jeweils ein Token, Dekodierung Prozess Beim autoregressiven Dekodierungsprozess mit jeweils einem Token besteht der Abfragevektor aus einem einzelnen Token. Es ist aufschlussreich, sich vorzustellen, wie eine Aufmerksamkeitsschicht in diesem Fall aussehen würde – eine einzelne Einbettungsreihe über einer riesigen gekachelten Ebene aus Gewichten. Diese Ansicht betont nicht nur die enorme Bedeutung von Gewichten im Vergleich zu Aktivierungen, sondern erinnert auch an die Vorstellung, dass K_t und V ähnlich wie dynamisch generierte Schichten in einem 6-Schicht-MLP funktionieren, obwohl die Mux/Demux-Berechnungen diese Entsprechung ungenau machen können: 7 LoRA Das aktuelle LoRA-Papier „LoRA: Low-Rank Adaptation of Large Language Models“ beschreibt eine effiziente Feinabstimmungstechnik basierend auf der Idee: Die während der Feinabstimmung eingeführten Gewichte δ sind niedrigrangig . Dem Papier zufolge „ermöglicht uns dies, indirekt einige dichte Schichten in einem neuronalen Netzwerk zu trainieren, indem wir die Rangzerlegungsmatrix der dichten Schichtänderungen während der Anpassung optimieren … und gleichzeitig die vorab trainierten Gewichte eingefroren lassen 7a Grundlagen.“ Idee Kurz gesagt besteht der entscheidende Schritt darin, die Faktoren der Gewichtsmatrix und nicht die Matrix selbst zu trainieren: Ersetzen Sie den I x J-Gewichtungstensor durch einen I x K-Tensor und die Matrixmultiplikation des K x J-Tensors, wobei Stellen Sie sicher, dass K ein kleiner Wert ist. Wenn K klein genug ist, kann es in Bezug auf die Größe einen großen Gewinn geben, aber es gibt Kompromisse: Durch die Reduzierung von K verringert sich auch der Rang, den das Produkt ausdrücken kann. Die Größeneinsparungen und strukturellen Auswirkungen auf die Ergebnisse werden hier anhand eines Beispiels veranschaulicht, hier einer zufälligen Matrixmultiplikation von 128 x 4 linken Parametern und 4 x 128 rechten Parametern – also einer 128 x 128-Matrix mit Rang-4-Bruch runter. Beachten Sie die vertikalen und horizontalen Muster in L@R: 7b Wenden Sie LoRA auf den Aufmerksamkeitskopf an. Die Art und Weise, wie LoRA diese Zerlegungsmethode auf den Feinabstimmungsprozess anwendet, ist: für jeden Gewichtstensor erstellt eine Zerlegung mit niedrigem Rang zur Feinabstimmung und trainiert ihre Faktoren, während die ursprünglichen Gewichte eingefroren bleiben. Multiplizieren Sie nach der Feinabstimmung jedes Paar von Faktoren mit niedrigem Rang, um eine Matrix in der Form des ursprünglichen Gewichts zu erhalten Tensor, und fügen Sie dies dem ursprünglichen vorab trainierten Gewichtstensor hinzu. Die folgende Visualisierung zeigt einen Aufmerksamkeitskopf mit seinen Gewichtungstensoren wQ, wK_t, wV, wO, ersetzt durch niedrigrangige Zerlegungen wQ_A @ wQ_B usw. Optisch erscheint die Faktormatrix als niedriger Zaun entlang der Kante des Windmühlenflügels: 

 Hier ist ein weiterer Modus, der Vektor-Matrix-Produkte verwendet, um Intuition aufzubauen. Beispiel: Dies zeigt, dass die Identitätsmatrix wie ein in einem 45-Grad-Winkel platzierter Spiegel wirkt und die entsprechenden Parameter und Ergebnisse widerspiegelt:
Hier ist ein weiterer Modus, der Vektor-Matrix-Produkte verwendet, um Intuition aufzubauen. Beispiel: Dies zeigt, dass die Identitätsmatrix wie ein in einem 45-Grad-Winkel platzierter Spiegel wirkt und die entsprechenden Parameter und Ergebnisse widerspiegelt: 






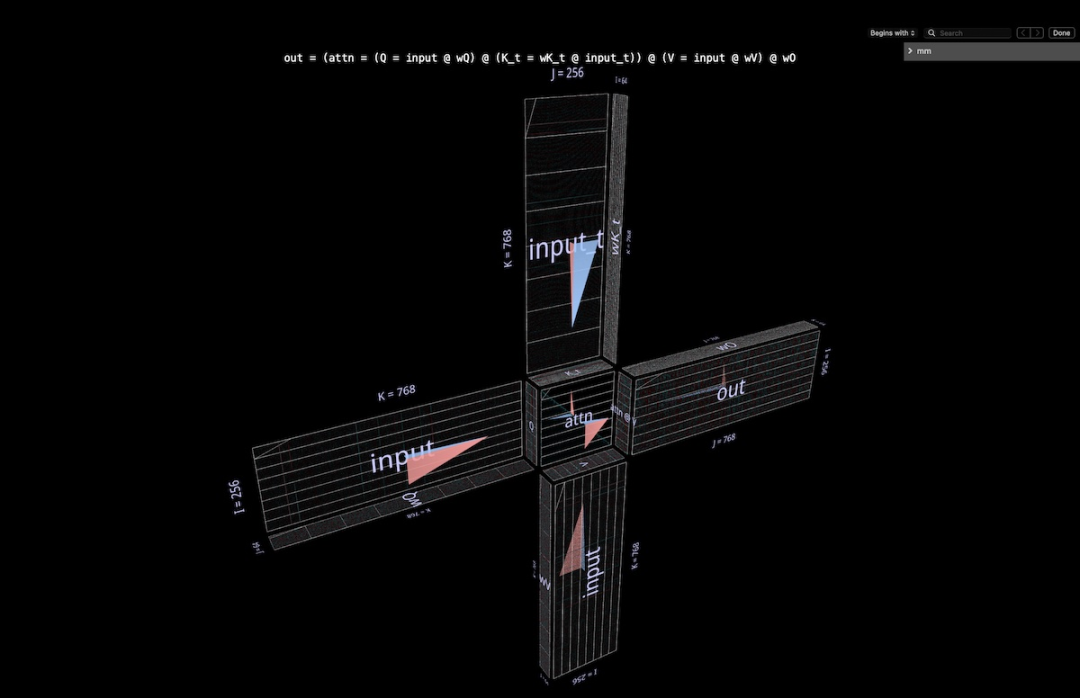
Q = input @ wQ// 1K_t = wK_t @ input_t// 2V = input @ wV// 3attn = sdpa(Q @ K_t)// 4head_out = attn @ V // 5out = head_out @ wO // 6
sdpa (input @ wQ @ K_t) @ V @ wO











Das obige ist der detaillierte Inhalt vonEinblick in die Matrixmultiplikation aus 3D-Perspektive, so sieht KI-Denken aus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

