Vielseitiger und effektiver: Ants selbst entwickelter Optimierer WSAM wurde für KDD Oral ausgewählt

Die Generalisierungsfähigkeit tiefer neuronaler Netze (DNNs) hängt eng mit der Flachheit der Extrempunkte zusammen. Daher wurde der Sharpness-Aware Minimization (SAM)-Algorithmus entwickelt, um flachere Extrempunkte zu finden und so die Generalisierungsfähigkeit zu verbessern. In diesem Artikel wird die Verlustfunktion von SAM erneut untersucht und eine allgemeinere und effektivere Methode, WSAM, vorgeschlagen, um die Ebenheit von Trainingsextrempunkten zu verbessern, indem Ebenheit als Regularisierungsbegriff verwendet wird. Experimente mit verschiedenen öffentlichen Datensätzen zeigen, dass WSAM im Vergleich zum ursprünglichen Optimierer SAM und seinen Varianten in den allermeisten Fällen eine bessere Generalisierungsleistung erzielt. WSAM wurde auch in den internen digitalen Zahlungs-, digitalen Finanz- und anderen Szenarien von Ant weit verbreitet und hat bemerkenswerte Ergebnisse erzielt. Diese Arbeit wurde von KDD '23 als mündliche Arbeit angenommen. ?? telligent - machine-learning/dlrover/tree/master/atorch/atorch/optimizers

Mit der Entwicklung der Deep-Learning-Technologie haben stark überparametrisierte DNNs großartige Ergebnisse in verschiedenen maschinellen Lernszenarien wie CV und NLP erzielt. Erfolg. Obwohl überparametrisierte Modelle dazu neigen, die Trainingsdaten zu stark anzupassen, verfügen sie in der Regel über gute Generalisierungsfähigkeiten. Das Geheimnis der Verallgemeinerung hat immer mehr Aufmerksamkeit erregt und ist zu einem beliebten Forschungsthema im Bereich Deep Learning geworden.

Die neuesten Forschungsergebnisse zeigen, dass die Generalisierungsfähigkeit eng mit der Ebenheit der Extrempunkte zusammenhängt. Mit anderen Worten: Das Vorhandensein flacher Extrempunkte in der „Landschaft“ der Verlustfunktion ermöglicht kleinere Generalisierungsfehler. Sharpness-Aware Minimization (SAM) [1] ist eine Technik zum Finden flacherer Extrempunkte und gilt derzeit als eine der vielversprechendsten technischen Richtungen. Die SAM-Technologie ist in vielen Bereichen wie Computer Vision, Verarbeitung natürlicher Sprache und zweischichtigem Lernen weit verbreitet und übertrifft bisherige hochmoderne Methoden in diesen Bereichen deutlich definiert eine Verlustfunktion. Die Ebenheit von

L

bei w ist wie folgt:
• GSAM [2] hat bewiesen, dass eine Näherung des maximalen Eigenwerts der Hesse-Matrix am lokalen Extrempunkt ist, was darauf hinweist das ist in der Tat eine flache (steile) effektive Messung. Allerdings kann
nur verwendet werden, um flachere Bereiche statt minimaler Punkte zu finden, was dazu führen kann, dass die Verlustfunktion zu einem Punkt konvergiert, an dem der Verlustwert immer noch groß ist (obwohl der umgebende Bereich flach ist). Daher verwendet SAM

, also

als Verlustfunktion. Es kann als Kompromiss zwischen der Suche nach einer flacheren Oberfläche und einem kleineren Verlustwert zwischen und

angesehen werden, wobei beiden das gleiche Gewicht beigemessen wird.

Dieser Artikel überdenkt die Konstruktion von 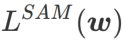und behandelt 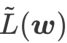als Regularisierungsbegriff. Wir haben einen allgemeineren und effektiveren Algorithmus namens WSAM (Weighted Sharpness-Aware Minimization) entwickelt. Seine Verlustfunktion fügt einen gewichteten Ebenheitsterm 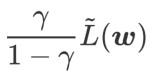als Regularisierungsterm hinzu, bei dem der Hyperparameter 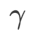die Ebenheitsgewichtung steuert. Im Kapitel zur Methodeneinführung haben wir gezeigt, wie man 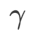verwendet, um die Verlustfunktion zu steuern, um flachere oder kleinere Extrempunkte zu finden. Unsere wichtigsten Beiträge lassen sich wie folgt zusammenfassen.

• Wir schlagen WSAM vor, das Flachheit als Regularisierungsbegriff behandelt und unterschiedliche Gewichtungen zwischen verschiedenen Aufgaben angibt. Wir schlagen eine Technik der „Gewichtungsentkopplung“ vor, um den Regularisierungsterm in der Aktualisierungsformel zu handhaben, mit dem Ziel, die Flachheit des aktuellen Schritts genau wiederzugeben. Wenn der zugrunde liegende Optimierer nicht SGD ist, wie z. B. SGDM und Adam, unterscheidet sich WSAM in seiner Form erheblich von SAM. Ablationsexperimente zeigen, dass diese Technik in den meisten Fällen die Leistung verbessert.
• Wir haben die Wirksamkeit von WSAM bei allgemeinen Aufgaben in öffentlichen Datensätzen überprüft. Experimentelle Ergebnisse zeigen, dass WSAM im Vergleich zu SAM und seinen Varianten in den meisten Situationen eine bessere Generalisierungsleistung aufweist.

Vorkenntnisse

SAM ist eine Technik zur Lösung des Minimax-Optimierungsproblems von 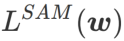, definiert durch Formel (1).

Erstens verwendet SAM eine Taylor-Erweiterung erster Ordnung um w, um das Maximierungsproblem der inneren Schicht zu approximieren, d. Das heißt,

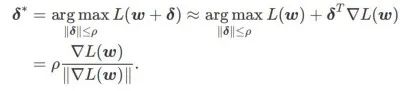
Die zweite Näherung besteht darin, die Berechnung zu beschleunigen. Andere Gradienten-basierte Optimierer (sogenannte Basisoptimierer) können in das allgemeine Framework von SAM integriert werden, Einzelheiten finden Sie unter Algorithmus 1. Durch Ändern von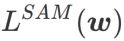

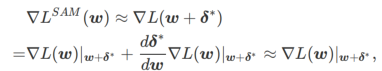
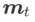
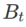
und

in Algorithmus 1 können wir verschiedene grundlegende Optimierer wie SGD, SGDM und Adam erhalten, siehe Tab. 1. Beachten Sie, dass Algorithmus 1 auf das ursprüngliche SAM aus dem SAM-Papier [1] zurückgreift, wenn der Basisoptimierer SGD ist.

Einführung in die Methode

Designdetails von WSAM

Hier geben wir die formale Definition von

, die aus einem regulären Verlust- und einem Flachheitsterm besteht. Aus Formel (1) ergibt sich

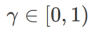Unter ihnen . Wenn 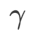=0, 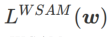zu einem regulären Verlust degeneriert; wenn 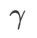=1/2, ist 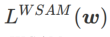äquivalent zu 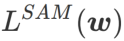; wenn 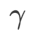>1/2, achtet 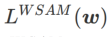mehr auf die Ebenheit, also ist es so Dasselbe wie bei SAM ist es einfacher, Punkte mit kleineren Krümmungen zu finden als mit kleineren Verlustwerten und umgekehrt.

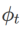Ein allgemeines Framework für WSAM, das verschiedene Basisoptimierer enthält, kann durch Auswahl verschiedener und 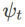implementiert werden, siehe Algorithmus 2. Wenn beispielsweise und 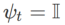sind, erhalten wir WSAM, dessen Basisoptimierer SGD ist, siehe Algorithmus 3. Hier wenden wir eine Technik der „Gewichtungsentkopplung“ an, bei der der Flachheitsterm nicht in den Basisoptimierer zur Berechnung von Gradienten und Aktualisierung von Gewichten integriert wird, sondern unabhängig berechnet wird (der letzte Term in Zeile 7 von Algorithmus 2). Auf diese Weise spiegelt der Regularisierungseffekt nur die Flachheit des aktuellen Schritts ohne zusätzliche Informationen wider. Zum Vergleich: Algorithmus 4 ergibt einen WSAM ohne „Gewichtsentkopplung“ (Coupled-WSAM genannt). Wenn der zugrunde liegende Optimierer beispielsweise SGDM ist, ist der Regularisierungsterm von Coupled-WSAM ein exponentieller gleitender Durchschnitt der Flachheit. Wie im experimentellen Teil gezeigt, kann die „Gewichtsentkopplung“ in den meisten Fällen die Generalisierungsleistung verbessern.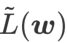

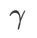Abb. 1 zeigt den WSAM-Update-Prozess unter verschiedenen Werten. Wenn 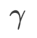, liegt

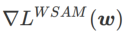zwischen 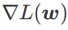und 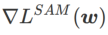und weicht mit zunehmendem 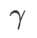allmählich von 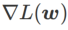ab.

Einfaches Beispiel

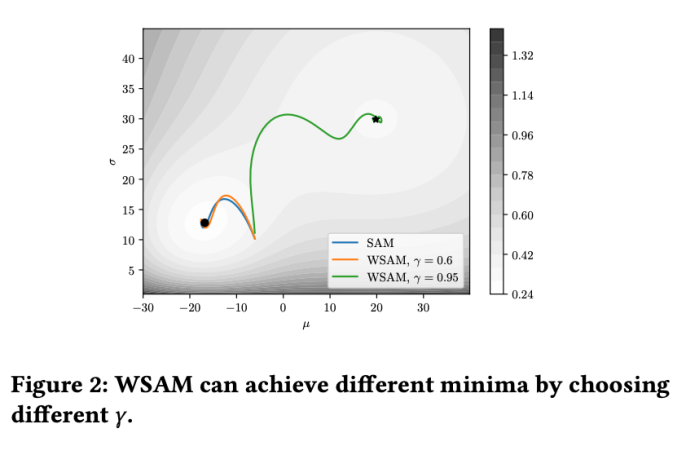
Um die Wirkung und Vorteile von γ in WSAM besser zu veranschaulichen, haben wir ein zweidimensionales einfaches Beispiel erstellt. Wie in Abb. 2 gezeigt, hat die Verlustfunktion einen relativ ungleichmäßigen Extrempunkt in der unteren linken Ecke (Position: (-16,8, 12,8), Verlustwert: 0,28) und einen flachen Extrempunkt in der oberen rechten Ecke (Position: (19,8, 29,9), Verlustwert: 0,36). 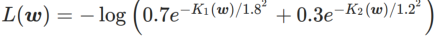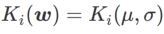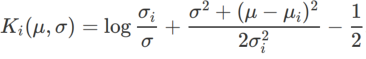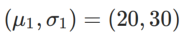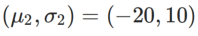Die Verlustfunktion ist definiert als: , wobei die KL-Divergenz zwischen dem univariaten Gaußschen Modell und zwei Normalverteilungen ist, also , wobei und ist.

Wir verwenden SGDM mit einem Impuls von 0,9 als Basisoptimierer und setzen 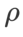=2 für SAM und WSAM. Ausgehend vom Anfangspunkt (-6, 10) wird die Verlustfunktion in 150 Schritten mit einer Lernrate von 5 optimiert. SAM konvergiert zum Extrempunkt mit geringerem Verlustwert, aber ungleichmäßiger, ähnlich wie WSAM mit 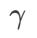=0,6. Allerdings führt 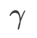=0,95 dazu, dass die Verlustfunktion zu einem flachen Extrempunkt konvergiert, was darauf hindeutet, dass eine stärkere Flatness-Regularisierung eine Rolle spielt.

Experimente

Wir haben Experimente zu verschiedenen Aufgaben durchgeführt, um die Wirksamkeit von WSAM zu überprüfen.

Bildklassifizierung

Wir haben zunächst die Wirkung von WSAM auf Trainingsmodelle von Grund auf an den Datensätzen Cifar10 und Cifar100 untersucht. Zu den von uns ausgewählten Modellen gehören ResNet18 und WideResNet-28-10. Wir trainieren Modelle auf Cifar10 und Cifar100 mit vordefinierten Batchgrößen von 128 bzw. 256 für ResNet18 bzw. WideResNet-28-10. Der hier verwendete Basisoptimierer ist SGDM mit einem Impuls von 0,9. Gemäß den Einstellungen von SAM [1] führt jeder Basisoptimierer doppelt so viele Epochen aus wie der SAM-Klassenoptimierer. Wir haben beide Modelle für 400 Epochen trainiert (200 Epochen für den SAM-Klassenoptimierer) und einen Cosinus-Scheduler verwendet, um die Lernrate zu verringern. Hier verwenden wir keine anderen erweiterten Datenerweiterungsmethoden wie Cutout und AutoAugment.

Für beide Modelle verwenden wir eine gemeinsame Rastersuche, um die Lernrate und den Gewichtsabfallkoeffizienten des Basisoptimierers zu bestimmen und sie für die folgenden Experimente mit dem SAM-Klassenoptimierer konstant zu halten. Die Suchbereiche für Lernrate und Gewichtsabfallkoeffizient sind {0,05, 0,1} bzw. {1e-4, 5e-4, 1e-3}. Da alle SAM-Klassenoptimierer einen Hyperparameter 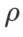(Nachbarschaftsgröße) haben, suchen wir als nächstes nach dem besten 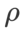auf dem SAM-Optimierer und verwenden denselben Wert für andere SAM-Klassenoptimierer. Der Suchbereich von 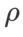ist {0,01, 0,02, 0,05, 0,1, 0,2, 0,5}. Schließlich suchten wir nach den einzigartigen Hyperparametern anderer SAM-Klassenoptimierer und der Suchbereich entstammte dem empfohlenen Bereich ihrer jeweiligen Originalartikel. Für GSAM [2] suchen wir im Bereich {0,01, 0,02, 0,03, 0,1, 0,2, 0,3}. 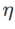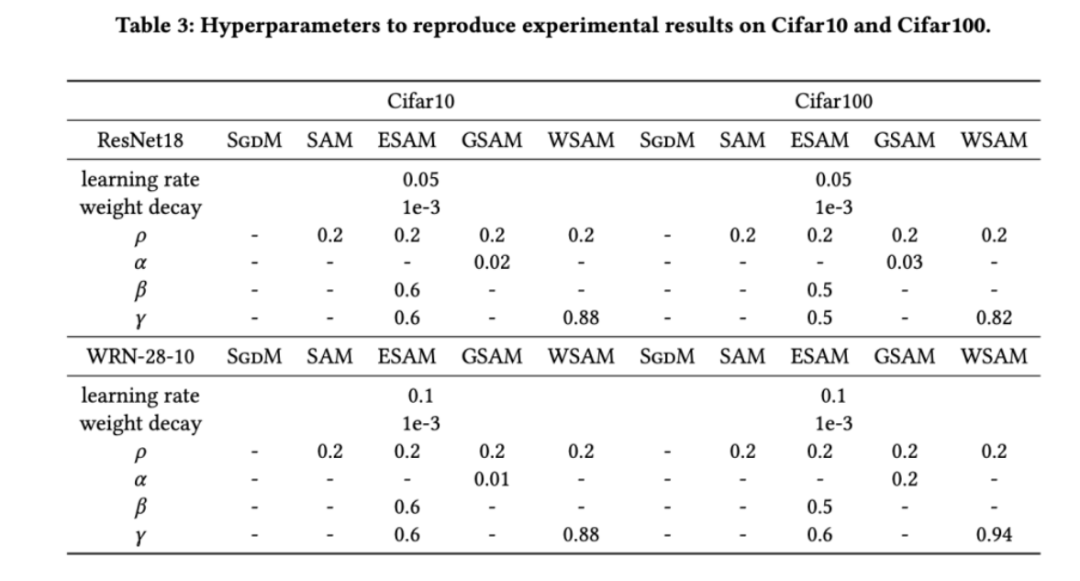Für ESAM [3] suchen wir nach im Bereich von {0,4, 0,5, 0,6}, im Bereich von {0,4, 0,5, 0,6} und 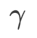im Bereich von {0,4, 0,5 , 0,6}. Für WSAM suchen wir nach im Bereich {0,5, 0,6, 0,7, 0,8, 0,82, 0,84, 0,86, 0,88, 0,9, 0,92, 0,94, 0,96}. Wir haben das Experiment fünfmal mit verschiedenen Zufallsstartwerten wiederholt und den mittleren Fehler und die Standardabweichung berechnet. Wir führen Experimente mit einer Einzelkarten-NVIDIA A100-GPU durch. Die Optimierer-Hyperparameter für jedes Modell sind in Tab. 3 zusammengefasst.

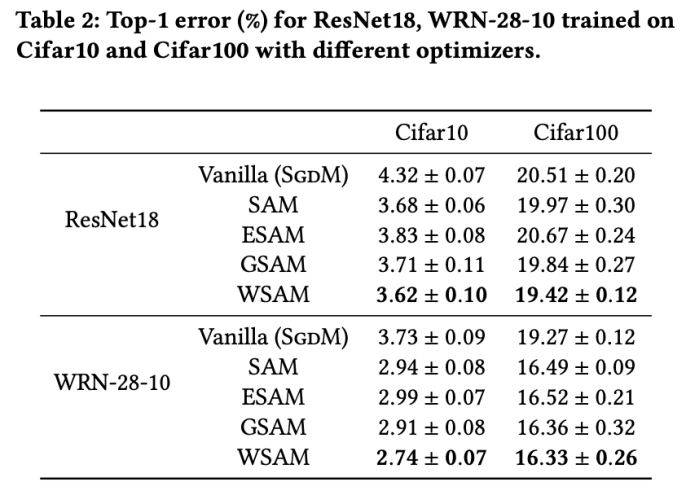
Tab. 2 zeigt die Top-1-Fehlerrate von ResNet18, WRN-28-10 im Testsatz auf Cifar10 und Cifar100 unter verschiedenen Optimierern. Im Vergleich zum Basisoptimierer verbessert der SAM-Klassenoptimierer die Leistung erheblich. Gleichzeitig ist WSAM deutlich besser als andere SAM-Klassenoptimierer.

Zusätzliche Schulung zu ImageNet

Wir führen außerdem Experimente mit dem ImageNet-Datensatz unter Verwendung der Netzwerkstruktur Data-Efficient Image Transformers durch. Wir nehmen einen vorab trainierten DeiT-Basiskontrollpunkt wieder auf und trainieren dann drei Epochen lang weiter. Das Modell wird mit einer Stapelgröße von 256 trainiert, der Basisoptimierer ist SGDM mit Impuls 0,9, der Gewichtsabfallkoeffizient beträgt 1e-4 und die Lernrate beträgt 1e-5. Wir haben den Lauf fünfmal auf einer NVIDIA A100-GPU mit vier Karten wiederholt und den durchschnittlichen Fehler und die Standardabweichung berechnet. Wir haben nach dem besten SAM in {0,05, 0,1, 0,5, 1,0,⋯, 6,0} gesucht. . Das Optimum

=5,5 wird direkt in anderen SAM-Klassenoptimierern verwendet. Danach suchen wir nach dem besten

von GSAM in {0,01, 0,02, 0,03, 0,1, 0,2, 0,3} und dem besten 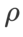von WSAM zwischen 0,80 und 0,98 mit einer Schrittweite von 0,02.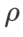 Die anfängliche Top-1-Fehlerrate des Modells beträgt 18,2 %, und nach drei weiteren Epochen ist die Fehlerrate in Tab. 4 dargestellt. Wir finden keine signifikanten Unterschiede zwischen den drei SAM-ähnlichen Optimierern, aber sie übertreffen alle den Basisoptimierer, was darauf hindeutet, dass sie flachere Extrempunkte finden können und über bessere Generalisierungsfähigkeiten verfügen.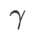

Robustheit gegenüber Label-Rauschen

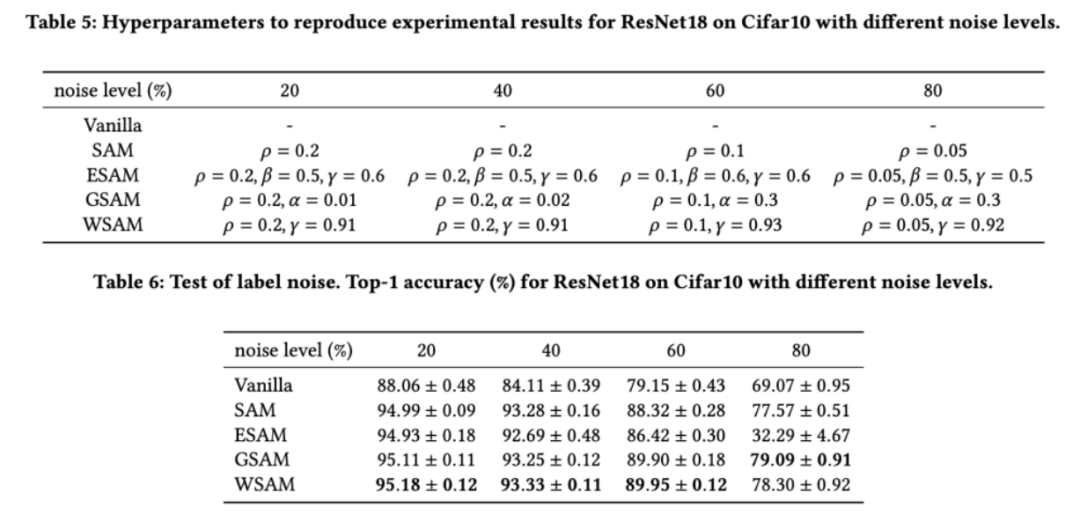
Wie in früheren Studien [1, 4, 5] gezeigt, zeigen SAM-Klassenoptimierer eine gute Robustheit, wenn Label-Rauschen im Trainingssatz vorhanden ist. Hier vergleichen wir die Robustheit von WSAM mit SAM, ESAM und GSAM. Wir trainieren ResNet18 auf dem Cifar10-Datensatz für 200 Epochen und injizieren symmetrisches Label-Rauschen mit Rauschpegeln von 20 %, 40 %, 60 % und 80 %. Wir verwenden SGDM mit einem Impuls von 0,9 als Basisoptimierer, einer Stapelgröße von 128, einer Lernrate von 0,05, einem Gewichtsabfallkoeffizienten von 1e-3 und einem Cosinus-Scheduler zum Abfallen der Lernrate. Für jeden Label-Rauschenpegel haben wir eine Rastersuche auf dem SAM im Bereich {0,01, 0,02, 0,05, 0,1, 0,2, 0,5} durchgeführt, um einen universellen 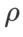-Wert zu ermitteln. Anschließend suchen wir einzeln nach anderen optimiererspezifischen Hyperparametern, um die optimale Generalisierungsleistung zu finden. Die zur Reproduktion unserer Ergebnisse erforderlichen Hyperparameter listen wir in Tab. 5 auf. Die Ergebnisse des Robustheitstests stellen wir in Tab. 6 dar. WSAM weist im Allgemeinen eine bessere Robustheit auf als SAM, ESAM und GSAM.

Auswirkungen der Explorationsgeometrie

SAM-ähnliche Optimierer können mit Techniken wie ASAM [4] und Fisher SAM [5] kombiniert werden, um die Form der Explorationsnachbarschaft adaptiv anzupassen. Wir führen Experimente zu WRN-28-10 auf Cifar10 durch, um die Leistung von SAM und WSAM bei Verwendung adaptiver bzw. Fisher-Informationsmethoden zu vergleichen und zu verstehen, wie sich die Geometrie der Explorationsregion auf die Generalisierungsleistung von SAM-ähnlichen Optimierern auswirkt.

Mit Ausnahme der Parameter 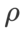und 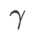haben wir die Konfiguration bei der Bildklassifizierung wiederverwendet. Laut früheren Studien [4, 5] sind die 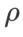von ASAM und Fisher SAM in der Regel größer. Wir suchen nach den besten 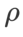in {0,1, 0,5, 1,0,…, 6,0}, und die besten 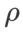für ASAM und Fisher SAM sind beide 5,0. Danach haben wir nach dem besten 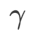von WSAM zwischen 0,80 und 0,94 mit einer Schrittweite von 0,02 gesucht, und der beste 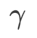beider Methoden war 0,88.

Überraschenderweise zeigt der Basis-WSAM, wie in Tab. 7 gezeigt, eine bessere Verallgemeinerung, selbst bei mehreren Kandidaten. Daher empfehlen wir, WSAM einfach mit einer festen 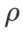Baseline zu verwenden.

Ablationsexperiment

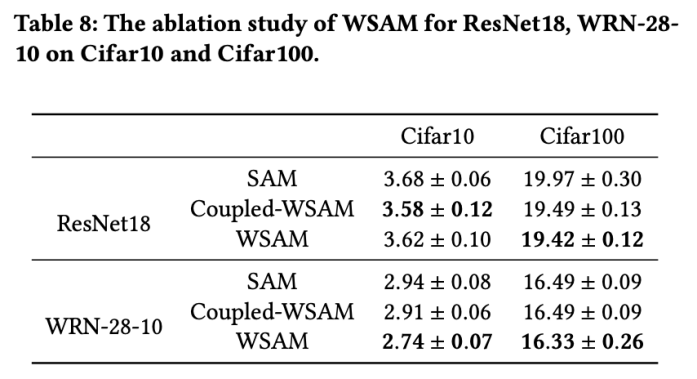
In diesem Abschnitt führen wir Ablationsexperimente durch, um ein tiefes Verständnis für die Bedeutung der „Gewichtsentkopplungstechnik“ bei WSAM zu erlangen. Wie in den Designdetails von WSAM beschrieben, vergleichen wir die WSAM-Variante ohne „Gewichtsentkopplung“ (Algorithmus 4) Coupled-WSAM mit der ursprünglichen Methode.

Die Ergebnisse sind in Tab. 8 dargestellt. Coupled-WSAM liefert in den meisten Fällen bessere Ergebnisse als SAM, und WSAM verbessert die Ergebnisse in den meisten Fällen noch weiter, was die Wirksamkeit der „Gewichtsentkopplungs“-Technik demonstriert.

Extrempunktanalyse

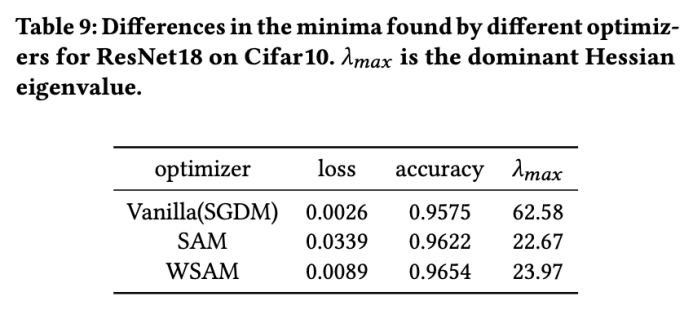
Hier vertiefen wir unser Verständnis des WSAM-Optimierers weiter, indem wir die Unterschiede zwischen den vom WSAM- und SAM-Optimierer gefundenen Extrempunkten vergleichen. Die Ebenheit (Steilheit) an Extrempunkten kann durch den maximalen Eigenwert der Hesse-Matrix beschrieben werden. Je größer der Eigenwert, desto weniger flach ist er. Wir verwenden den Power-Iteration-Algorithmus, um diesen maximalen Eigenwert zu berechnen.

Tab. 9 zeigt den Unterschied zwischen den von den SAM- und WSAM-Optimierern gefundenen Extrempunkten. Wir stellen fest, dass die vom Vanilla-Optimierer gefundenen Extrempunkte kleinere Verlustwerte aufweisen, aber weniger flach sind, während die von SAM gefundenen Extrempunkte größere Verlustwerte aufweisen, aber flacher sind, wodurch die Generalisierungsleistung verbessert wird. Interessanterweise weisen die von WSAM gefundenen Extrempunkte nicht nur viel kleinere Verlustwerte als SAM auf, sondern weisen auch eine Flachheit auf, die der von SAM sehr nahe kommt. Dies zeigt, dass WSAM bei der Suche nach Extrempunkten Priorität auf die Sicherstellung kleinerer Verlustwerte legt und gleichzeitig versucht, nach flacheren Bereichen zu suchen.

Hyperparameter-Sensitivität

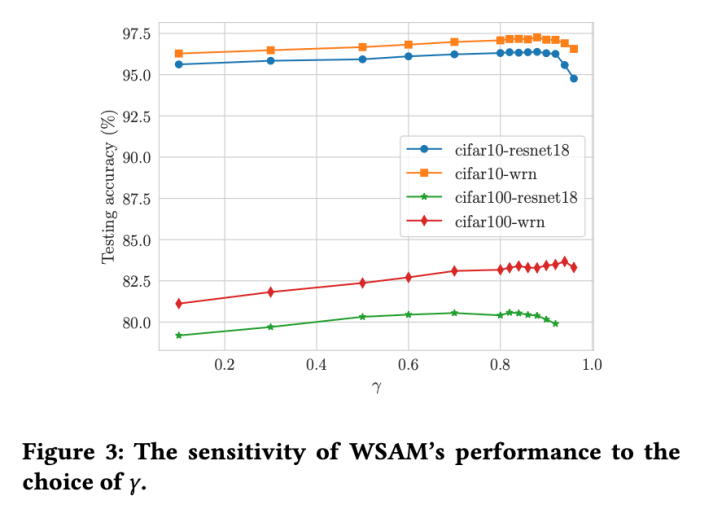
Im Vergleich zu SAM verfügt WSAM über einen zusätzlichen Hyperparameter 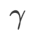zur Skalierung der Größe des flachen (steilen) Gradterms. Hier testen wir die Empfindlichkeit der Generalisierungsleistung von WSAM gegenüber diesem Hyperparameter. Wir haben ResNet18- und WRN-28-10-Modelle mit WSAM auf Cifar10 und Cifar100 trainiert und dabei eine breite Palette von 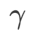-Werten verwendet. Wie in Abb. 3 dargestellt, zeigen die Ergebnisse, dass WSAM nicht empfindlich auf die Wahl des Hyperparameters 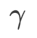reagiert. Wir haben außerdem herausgefunden, dass die optimale Generalisierungsleistung von WSAM fast immer zwischen 0,8 und 0,95 liegt.

Das obige ist der detaillierte Inhalt vonVielseitiger und effektiver: Ants selbst entwickelter Optimierer WSAM wurde für KDD Oral ausgewählt. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!