Heim >Technologie-Peripheriegeräte >KI >Hören Sie mir zu, Transformer ist eine Support-Vektor-Maschine
Hören Sie mir zu, Transformer ist eine Support-Vektor-Maschine
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-09-17 18:09:03817Durchsuche
Transformer ist eine Support Vector Machine (SVM), eine neue Theorie, die Diskussionen in der akademischen Gemeinschaft ausgelöst hat.
Letztes Wochenende wurde in einem Artikel der University of Pennsylvania und der University of California, Riverside versucht, die Prinzipien der Transformer-Struktur anhand großer Modelle, ihrer optimierten Geometrie in der Aufmerksamkeitsschicht und der Trennung optimaler Eingabe-Tokens zu untersuchen Es wird eine formale Äquivalenz zwischen den hart begrenzten SVM-Problemen hergestellt.
Der Autor erklärte auf Hackernews, dass diese Theorie das Problem löst, dass SVM in jeder Eingabesequenz „gute“ Token von „schlechten“ Token trennt. Als Token-Selektor mit hervorragender Leistung unterscheidet sich diese SVM wesentlich von der herkömmlichen SVM, die der Eingabe 0-1 Labels zuweist.
Diese Theorie erklärt auch, wie Aufmerksamkeit durch Softmax zu Sparsity führt: „schlechte“ Token, die auf der falschen Seite der SVM-Entscheidungsgrenze liegen, werden von der Softmax-Funktion unterdrückt, während „gute“ Token diejenigen sind, die am Ende nicht- Null-Softmax-Wahrscheinlichkeitstoken. Erwähnenswert ist auch, dass diese SVM von den exponentiellen Eigenschaften von Softmax abgeleitet ist.
Nachdem das Papier auf arXiv hochgeladen wurde, äußerten die Leute nacheinander ihre Meinung. Einige Leute sagten: Die Richtung der KI-Forschung dreht sich wirklich, wird sie wieder zurückgehen?
Nachdem sich der Kreis geschlossen hat, sind Support-Vektor-Maschinen immer noch nicht veraltet.
Seit der Veröffentlichung des Klassikers „Attention is All You Need“ hat die Transformer-Architektur revolutionäre Fortschritte auf dem Gebiet der Verarbeitung natürlicher Sprache (NLP) gebracht. Die Aufmerksamkeitsschicht in Transformer akzeptiert eine Reihe von Eingabe-Tokens 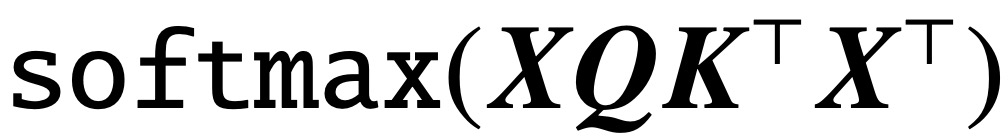 Jetzt stellt ein neues Papier mit dem Titel „Transformers as Support Vector Machines“ eine formale Äquivalenz zwischen der Optimierungsgeometrie der Selbstaufmerksamkeit und dem Hard-Margin-SVM-Problem her, indem das lineare äußere Produkt von Token-Paaren mit Einschränkungen optimale Eingabe-Token trennt von nicht optimalen Token.
Jetzt stellt ein neues Papier mit dem Titel „Transformers as Support Vector Machines“ eine formale Äquivalenz zwischen der Optimierungsgeometrie der Selbstaufmerksamkeit und dem Hard-Margin-SVM-Problem her, indem das lineare äußere Produkt von Token-Paaren mit Einschränkungen optimale Eingabe-Token trennt von nicht optimalen Token.
 Link zum Papier: https://arxiv.org/pdf/2308.16898.pdf
Link zum Papier: https://arxiv.org/pdf/2308.16898.pdf
Diese formale Äquivalenz basiert auf dem Papier „Max-Margin Token Selection in Attention Mechanism“ von Davoud Ataee Tarzanagh et al. „Auf der Grundlage der Vanishing-Regularisierung, Konvergenz zu einer SVM-Lösung, die die Kernnorm der kombinierten Parameter minimiert
. Im Gegensatz dazu minimiert die Parametrisierung direkt über W das SVM-Ziel der Frobenius-Norm. Der Artikel beschreibt diese Konvergenz und betont, dass sie eher in Richtung eines lokalen Optimums als in Richtung eines globalen Optimums auftreten kann.
(2) Der Artikel demonstriert auch die lokale/globale Richtungskonvergenz des W-Parametrisierungsgradientenabstiegs unter geeigneten geometrischen Bedingungen. Wichtig ist, dass die Überparametrisierung die globale Konvergenz katalysiert, indem sie die Machbarkeit des SVM-Problems sicherstellt und eine harmlose Optimierungsumgebung ohne stationäre Punkte gewährleistet. 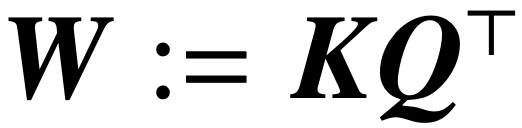 (3) Während die Theorie dieser Studie hauptsächlich auf lineare Vorhersageköpfe anwendbar ist, schlägt das Forschungsteam ein allgemeineres SVM-Äquivalent vor, das die implizite Vorspannung von 1-Schicht-Transformatoren mit nichtlinearen Köpfen/MLPs vorhersagen kann.
(3) Während die Theorie dieser Studie hauptsächlich auf lineare Vorhersageköpfe anwendbar ist, schlägt das Forschungsteam ein allgemeineres SVM-Äquivalent vor, das die implizite Vorspannung von 1-Schicht-Transformatoren mit nichtlinearen Köpfen/MLPs vorhersagen kann.
Im Allgemeinen sind die Ergebnisse dieser Studie auf allgemeine Datensätze anwendbar und können auf Aufmerksamkeitsebenen erweitert werden, und die praktische Gültigkeit der Studienschlussfolgerungen wurde durch gründliche numerische Experimente überprüft. Diese Studie begründet eine neue Forschungsperspektive, die mehrschichtige Transformatoren als SVM-Hierarchien betrachtet, die die besten Token trennen und auswählen.
Konkret analysiert diese Studie bei gegebener Eingabesequenz der Länge T und der Einbettungsdimension d
die Kernmodelle der Queraufmerksamkeit und Selbstaufmerksamkeit:

wobei K, Q, V jeweils trainierbare Schlüssel-, Abfrage- und Wertematrizen sind, 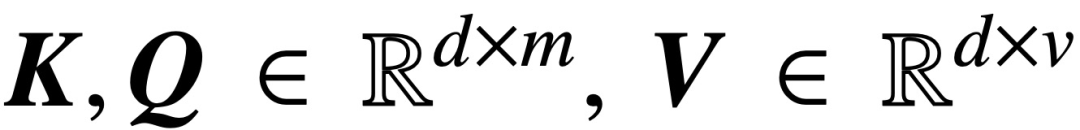 ; S (・) stellt Softmax-Nichtlinearität dar, die Zeile für Zeile angewendet wird
; S (・) stellt Softmax-Nichtlinearität dar, die Zeile für Zeile angewendet wird 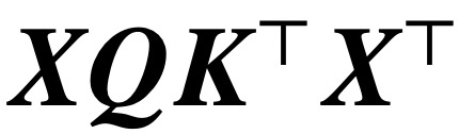 . Die Studie geht davon aus, dass der erste Token von Z (bezeichnet mit z) zur Vorhersage verwendet wird. Insbesondere bei einem Trainingsdatensatz
. Die Studie geht davon aus, dass der erste Token von Z (bezeichnet mit z) zur Vorhersage verwendet wird. Insbesondere bei einem Trainingsdatensatz 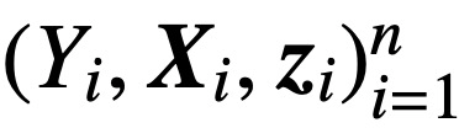 ,
, 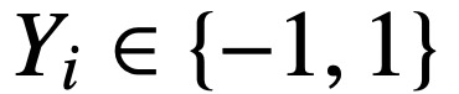 ,
, 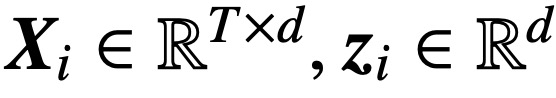 verwendet diese Studie die abnehmende Verlustfunktion
verwendet diese Studie die abnehmende Verlustfunktion  , um Folgendes zu minimieren:
, um Folgendes zu minimieren:
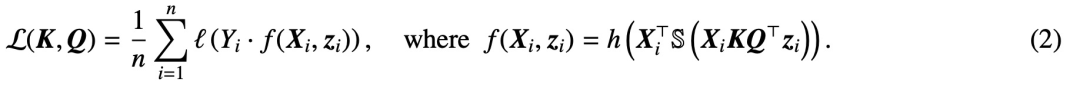
Hier h (・): 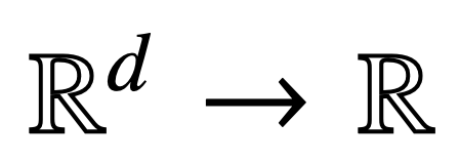 . ist Der Vorhersageheader enthält das Wertgewicht V. In dieser Formulierung stellt das Modell f (・) genau einen einschichtigen Transformator dar, bei dem auf die Aufmerksamkeitsschicht ein MLP folgt. Der Autor stellt die Selbstaufmerksamkeit in (2) wieder her, indem er
. ist Der Vorhersageheader enthält das Wertgewicht V. In dieser Formulierung stellt das Modell f (・) genau einen einschichtigen Transformator dar, bei dem auf die Aufmerksamkeitsschicht ein MLP folgt. Der Autor stellt die Selbstaufmerksamkeit in (2) wieder her, indem er 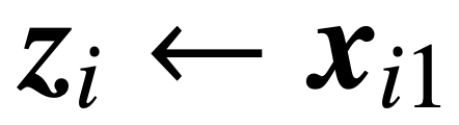 setzt, wobei x_i das erste Token der Sequenz X_i darstellt. Aufgrund der nichtlinearen Natur der Softmax-Operation stellt sie eine große Herausforderung für die Optimierung dar. Selbst wenn der Vorhersagekopf fest und linear ist, ist das Problem nicht konvex und nicht linear. In dieser Studie konzentrieren sich die Autoren auf die Optimierung der Aufmerksamkeitsgewichte (K, Q oder W) und die Bewältigung dieser Herausforderungen, um die grundlegende Äquivalenz von SVMs festzustellen.
setzt, wobei x_i das erste Token der Sequenz X_i darstellt. Aufgrund der nichtlinearen Natur der Softmax-Operation stellt sie eine große Herausforderung für die Optimierung dar. Selbst wenn der Vorhersagekopf fest und linear ist, ist das Problem nicht konvex und nicht linear. In dieser Studie konzentrieren sich die Autoren auf die Optimierung der Aufmerksamkeitsgewichte (K, Q oder W) und die Bewältigung dieser Herausforderungen, um die grundlegende Äquivalenz von SVMs festzustellen.
Die Struktur des Papiers ist wie folgt: Kapitel 2 stellt das vorläufige Wissen über Selbstaufmerksamkeit und Optimierung vor. Kapitel 3 analysiert die Optimierungsgeometrie der Selbstaufmerksamkeit und zeigt, dass der Aufmerksamkeitsparameter RP zur maximalen Randlösung konvergiert; Kapitel 4 und Kapitel 5 stellen die globale bzw. lokale Gradientenabstiegsanalyse vor und zeigen, dass die Schlüsselabfragevariable W zur Lösung von (Att-SVM) konvergiert. Kapitel 6 liefert Ergebnisse zur Äquivalenz von nichtlinearen Vorhersageköpfen und verallgemeinertem SVM 6 Kapitel 7 erweitert die Theorie auf sequentielle und kausale Vorhersagen; Kapitel 8 diskutiert die entsprechende Literatur. Abschließend schließt Kapitel 9 mit Vorschlägen für offene Fragen und zukünftige Forschungsrichtungen ab.
Der Hauptinhalt des Artikels lautet wie folgt:
Implizite Voreingenommenheit in der Aufmerksamkeitsschicht (Kapitel 2-3)
Optimierung der Aufmerksamkeitsparameter (K, Q), wenn die Regularisierung verschwindet, It konvergiert zur maximalen Randlösung von  in der Richtung, und sein nukleares Normziel ist der Kombinationsparameter
in der Richtung, und sein nukleares Normziel ist der Kombinationsparameter 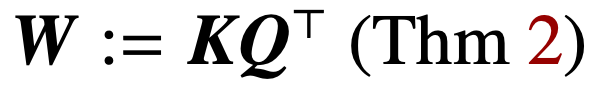 . Im Fall der direkten Parametrisierung der Queraufmerksamkeit mit dem kombinierten Parameter W konvergiert der Regularisierungspfad (RP) direktional zur (Att-SVM)-Lösung, die auf die Frobenius-Norm abzielt.
. Im Fall der direkten Parametrisierung der Queraufmerksamkeit mit dem kombinierten Parameter W konvergiert der Regularisierungspfad (RP) direktional zur (Att-SVM)-Lösung, die auf die Frobenius-Norm abzielt.
Dies ist das erste Ergebnis, das die parametrische Optimierungsdynamik von W und (K, Q) formal unterscheidet und Verzerrungen niedriger Ordnung in letzterer aufdeckt. Die Theorie dieser Studie beschreibt klar die Optimalität ausgewählter Token und erstreckt sich natürlich auf Sequenz-zu-Sequenz- oder kausale Klassifizierungseinstellungen.
Konvergenz des Gradientenabstiegs (Kapitel 4-5)
Bei entsprechender Initialisierung und linearem Kopf h (・) konvergieren Gradientenabstiegsiterationen (GD) der kombinierten Schlüssel-Abfragevariablen W in der Richtung zu die lokal optimale Lösung von (Att-SVM) (Abschnitt 5). Um ein lokales Optimum zu erreichen, muss der ausgewählte Token eine höhere Punktzahl haben als benachbarte Token.
Die lokal optimale Richtung ist nicht unbedingt eindeutig und kann anhand der geometrischen Eigenschaften des Problems bestimmt werden [TLZO23]. Als wichtigen Beitrag identifizieren die Autoren geometrische Bedingungen, die die Konvergenz in Richtung des globalen Optimums gewährleisten (Kapitel 4). Zu diesen Bedingungen gehören:
- Der beste Token weist einen deutlichen Unterschied in der Punktzahl auf.
- Die anfängliche Gradientenrichtung stimmt mit dem besten Token überein.
Darüber hinaus zeigt das Papier auch, dass eine Überparametrisierung (d. h. die Dimension d ist groß und die gleichen Bedingungen gelten) durch Sicherstellung der Durchführbarkeit von (1) (Att-SVM) und (2) harmlos ist Optimierungslandschaft (d. h. es gibt keine stationären Punkte und falschen lokalen optimalen Richtungen), um die globale Konvergenz zu katalysieren (siehe Abschnitt 5.2).
Die Abbildungen 1 und 2 veranschaulichen dies.
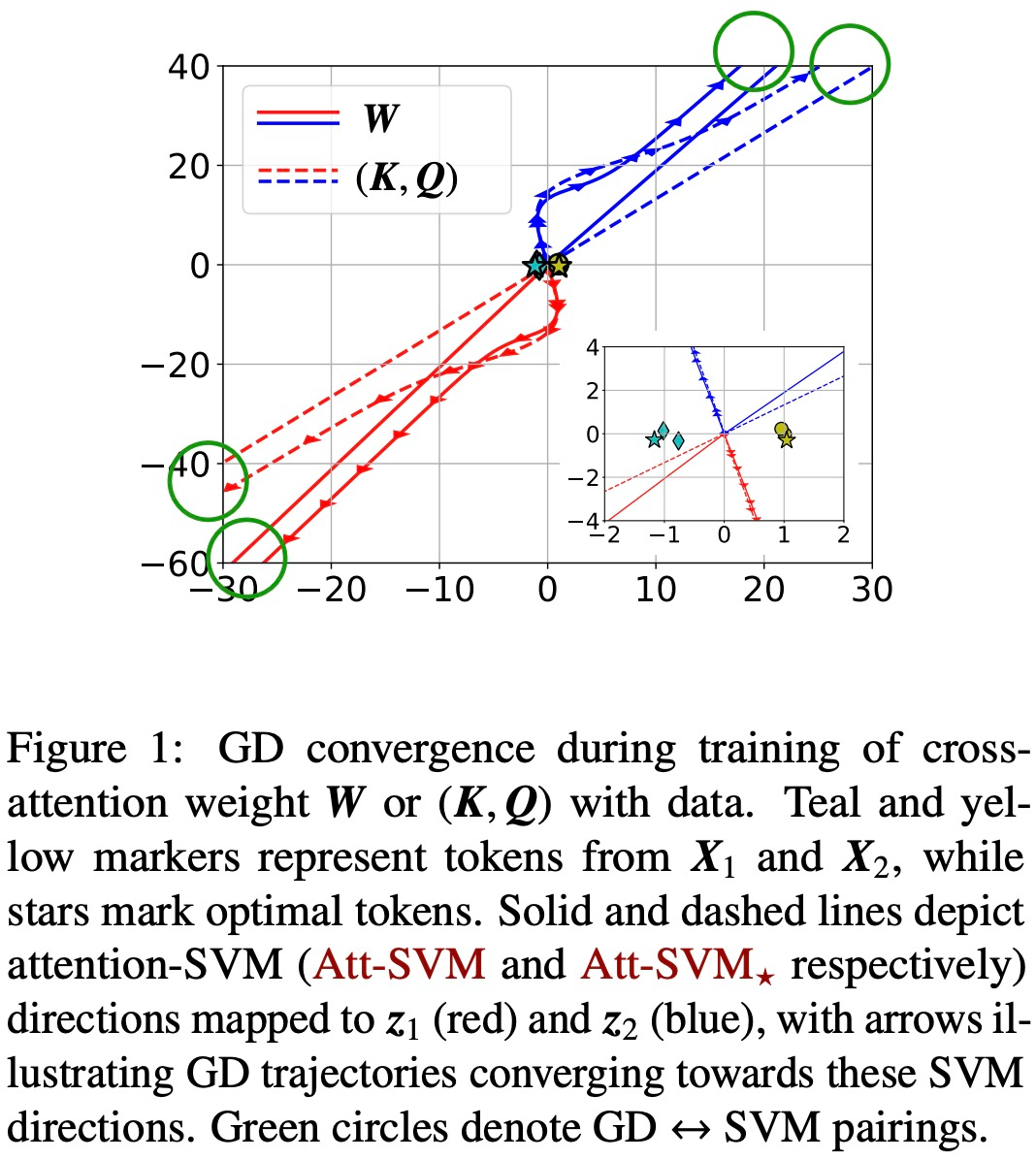
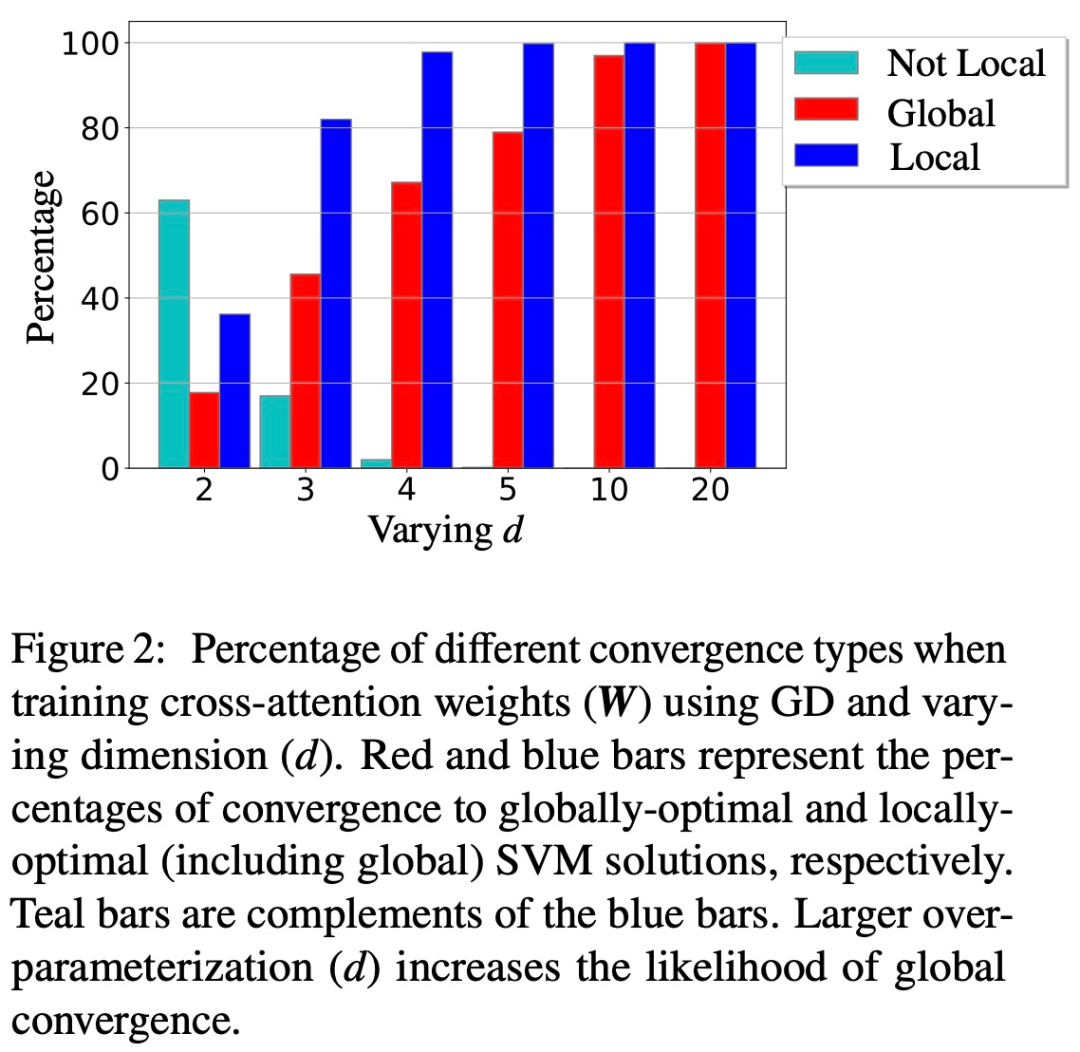
Allgemeingültigkeit des SVM-Äquivalents (Kapitel 6)
Bei der Optimierung mit linearem h (・) Grundvoreingenommenheit zur Auswahl eines Tokens jede Sequenz (auch bekannt als harte Aufmerksamkeit). Dies spiegelt sich in (Att-SVM) wider, wo der Ausgabetoken eine konvexe Kombination der Eingabetoken ist. Im Gegensatz dazu zeigen die Autoren, dass nichtlineare Köpfe aus mehreren Token bestehen müssen, was ihre Bedeutung für die Transformatordynamik hervorhebt (Abschnitt 6.1). Basierend auf Erkenntnissen aus der Theorie schlagen die Autoren einen allgemeineren äquivalenten Ansatz für SVM vor.
Sie zeigen insbesondere, dass unsere Methode die implizite Tendenz der durch Gradientenabstieg trainierten Aufmerksamkeit in allgemeinen Fällen, die nicht von der Theorie abgedeckt werden (z. B. h (・) ist ein MLP), genau vorhersagen kann. Konkret entkoppelt unsere allgemeine Formel das Aufmerksamkeitsgewicht in zwei Teile: einen von SVM gesteuerten Richtungsteil, der Marker durch Anwenden einer 0-1-Maske auswählt, und einen endlichen Teil, der die Softmax-Wahrscheinlichkeit anpasst, die die genaue Zusammensetzung des ausgewählten Tokens bestimmt;
Ein wichtiges Merkmal dieser Erkenntnisse ist, dass sie auf beliebige Datensätze anwendbar sind (sofern SVM machbar ist) und numerisch verifiziert werden können. Die Autoren haben die maximale Randäquivalenz und die implizite Vorspannung des Transformators ausführlich experimentell überprüft. Die Autoren glauben, dass diese Ergebnisse zum Verständnis von Transformatoren als hierarchischem Token-Auswahlmechanismus mit maximaler Marge beitragen und den Grundstein für kommende Forschungen zu ihrer Optimierungs- und Generalisierungsdynamik legen können.
Das obige ist der detaillierte Inhalt vonHören Sie mir zu, Transformer ist eine Support-Vektor-Maschine. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Welche sind die am häufigsten verwendeten relationalen Datenbanken?
- Gehen die im RAM gespeicherten Daten nach einem Stromausfall verloren?
- Was soll ich tun, wenn WPS-Text die Datenquelle nicht öffnen kann?
- Was sind in der Datenbanktechnologie die vier wichtigsten Datenmodelle?
- Welche Protokolle gehören zur Anwendungsschicht im TCP-IP-Referenzmodell?

