Heim >Backend-Entwicklung >C++ >C-Programm für Mäuse im Labyrinth – Backtracking-2
C-Programm für Mäuse im Labyrinth – Backtracking-2
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-09-11 14:25:21704Durchsuche
Die Ratte im Labyrinth ist auch ein häufiges Problem beim Backtracking. I
Ein Labyrinth ist eine zweidimensionale Matrix, in der einige Zellen blockiert sind. Eine der Zellen ist die Quellzelle und wir müssen von dort aus beginnen. Eine weitere davon ist das Ziel, der Ort, an den wir gelangen müssen. Wir müssen einen Weg von der Quelle zum Ziel finden, ohne blockierte Zellen zu betreten. Unten sehen Sie ein Bild des ungelösten Labyrinths.

Das ist die Lösung dafür.
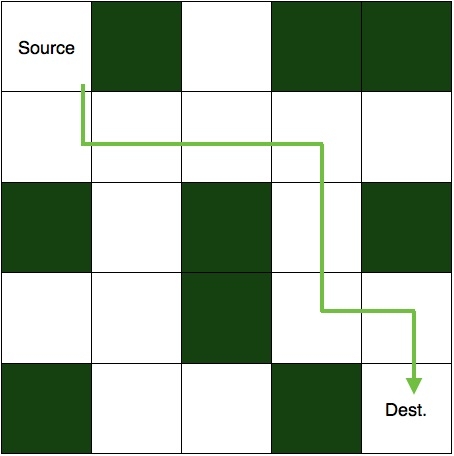
Um dieses Rätsel zu lösen, beginnen wir zunächst bei der Quelleinheit und bewegen uns in die Richtung, in der der Weg nicht blockiert ist. Führt uns der eingeschlagene Weg zum Ziel, ist das Rätsel gelöst. Andernfalls werden wir zurückkommen und die Richtung des eingeschlagenen Weges ändern. Wir werden die gleiche Logik auch im Code implementieren.
Input:
maze[][] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}}
Output:
1 0 0 0 0
1 1 1 1 0
0 0 0 1 0
0 0 0 1 1
0 0 0 0 1Erklärung
Zuerst erstellen wir eine Matrix zur Darstellung des Labyrinths. Die Elemente der Matrix sind 0 oder 1. 1 bedeutet blockierte Zellen und 0 bedeutet Zellen, die wir verschieben können. Die Matrix für das oben gezeigte Labyrinth lautet wie folgt:
0 1 0 1 1 0 0 0 0 0 1 0 1 0 1 0 0 1 0 0 1 0 0 1 0
Jetzt erstellen wir eine weitere Matrix mit denselben Abmessungen, um die Lösung zu speichern. Seine Elemente werden ebenfalls 0 oder 1 sein. 1 stellt die Zellen in unserem Pfad dar und die übrigen Zellen werden 0 sein. Die Matrix, die die Lösung darstellt, ist:
1 0 0 0 0 1 1 1 1 0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1
So, jetzt haben wir unsere Matrix. Als nächstes werden wir den Pfad von der Startzelle zur Zielzelle finden. Die Schritte, die wir unternehmen werden, sind wie folgt:
Überprüfen Sie die aktuelle Zelle. Wenn es sich um die Zielzelle handelt, ist das Rätsel gelöst.
Wenn nicht, versuchen Sie, nach unten zu gehen und prüfen Sie, ob Sie zur nächsten Zelle wechseln können (um zu einer Zelle zu wechseln, muss diese leer sein und darf sich nicht im Pfad befinden).
Wenn Sie zur nächsten Zelle wechseln können, bewegen Sie sich weiter auf dem Pfad zur nächstniedrigeren Zelle.
Wenn nicht, versuchen Sie, nach rechts zu gehen. Wenn die rechte Seite blockiert oder besetzt ist, bewegen Sie sich nach oben.
Wenn ein Aufsteigen nicht möglich ist, bewegen wir uns ebenfalls einfach in die linke Zelle.
Wenn eine Bewegung in eine der vier Richtungen (unten, rechts, oben oder links) nicht möglich ist, gehen Sie einfach zurück und ändern Sie den aktuellen Pfad (Backtracking).
Um es zusammenzufassen: Wir versuchen, von der aktuellen Zelle zu anderen Zellen zu wechseln (nach unten, rechts, oben und links). Wenn keine Bewegung möglich ist, gehen wir zurück und ändern die Richtung des Pfads zu einem anderen Zellengitter.
printsolution → Diese Funktion druckt nur die Lösungsmatrix.
solvemaze → Dies ist die Funktion, die den Backtracking-Algorithmus tatsächlich implementiert. Zuerst prüfen wir, ob unsere Zelle die Zielzelle ist, wenn ja (r==SIZE-1) und (c==SIZE-1). Wenn es die Zielzelle ist, ist unser Rätsel gelöst. Wenn nicht, prüfen wir, ob es sich um eine gültige Mobilfunkzelle handelt. In der Matrix muss sich eine gültige Zelle befinden, d. h. der Index muss zwischen 0 und SIZE-1 liegen, r>=0 && c>=0 && r Das obige ist der detaillierte Inhalt vonC-Programm für Mäuse im Labyrinth – Backtracking-2. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!Beispiel
#include <iostream>
using namespace std;
#define SIZE 5
//the maze problem
int maze[SIZE][SIZE] = {
{0,1,0,1,1},
{0,0,0,0,0},
{1,0,1,0,1},
{0,0,1,0,0},
{1,0,0,1,0}
};
//matrix to store the solution
int solution[SIZE][SIZE];
//function to print the solution matrix
void printsolution() {
int i,j;
for(i=0;i<SIZE;i++) {
for(j=0;j<SIZE;j++) {
printf("%d\t",solution[i][j]);
}
printf("</p><p></p><p>");
}
}
//function to solve the maze
//using backtracking
int solvemaze(int r, int c) {
//if destination is reached, maze is solved
//destination is the last cell(maze[SIZE-1][SIZE-1])
if((r==SIZE-1) && (c==SIZE-1) {
solution[r][c] = 1;
return 1;
}
//checking if we can visit in this cell or not
//the indices of the cell must be in (0,SIZE-1)
//and solution[r][c] == 0 is making sure that the cell is not already visited
//maze[r][c] == 0 is making sure that the cell is not blocked
if(r>=0 && c>=0 && r<SIZE && c<SIZE && solution[r][c] == 0 && maze[r][c] == 0){
//if safe to visit then visit the cell
solution[r][c] = 1;
//going down
if(solvemaze(r+1, c))
return 1;
//going right
if(solvemaze(r, c+1))
return 1;
//going up
if(solvemaze(r-1, c))
return 1;
//going left
if(solvemaze(r, c-1))
return 1;
//backtracking
solution[r][c] = 0;
return 0;
}
return 0;
}
int main() {
//making all elements of the solution matrix 0
int i,j;
for(i=0; i<SIZE; i++) {
for(j=0; j<SIZE; j++) {
solution[i][j] = 0;
}
}
if (solvemaze(0,0))
printsolution();
else
printf("No solution</p><p>");
return 0;
}
In Verbindung stehende Artikel
Mehr sehen- C++-Kompilierungsfehler: Auf eine Header-Datei wird mehrfach verwiesen. Wie kann das Problem behoben werden?
- C++-Kompilierungsfehler: Falsche Funktionsparameter, wie kann man das beheben?
- C++-Fehler: Der Konstruktor muss im öffentlichen Bereich deklariert werden, wie gehe ich damit um?
- Prozessverwaltung und Thread-Synchronisation in C++
- Umgang mit Datenaufteilungsproblemen in der C++-Entwicklung

