In C das größte Reuleaux-Dreieck innerhalb eines Quadrats

Ein Lule-Dreieck ist eine Form, die durch den Schnittpunkt von drei Scheiben entsteht, wobei der Mittelpunkt jeder Scheibe auf der Grenze der anderen beiden Scheiben liegt. Sein Rand ist eine Kurve konstanter Breite und neben dem Kreis selbst die einfachste und bekannteste Kurve dieser Art. Konstante Breite bedeutet, dass der Abstand zwischen jeweils zwei parallelen Stützlinien unabhängig von ihrer Ausrichtung gleich ist. Weil alle Durchmesser gleich sind.

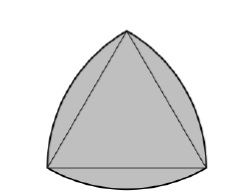
Die Grenze des Lule-Dreiecks ist eine Kurve konstanter Breite, die auf einem gleichseitigen Dreieck basiert. Alle Punkte einer Kante haben den gleichen Abstand vom gegenüberliegenden Scheitelpunkt.

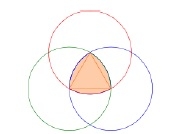
Konstruieren Sie ein Lule-Dreieck

Die Formel des Lule-Dreiecks

Wenn die Kurve auf einem gleichseitigen Dreieck basiert und die Seitenlänge des Dreiecks h ist, dann ist die Fläche des Lule-Dreiecks

A = (&pi; * h<sup>2</sup>) / 2 &ndash; 2 * (Area of equilateral triangle) = (&pi; &ndash; &radic;3) * h<sup>2</sup> / 2 = 0.70477 * h<sup>2</sup>

Finden Sie das Maximum innerhalb eines quadratischen Reuleaux-Dreiecks. Nehmen wir ein Beispiel parallele Linien, die das Reuleaux-Dreieck unterstützen.

Der Abstand zwischen den parallelen Linien, die das Reuleaux-Dreieck stützen = die Seitenlänge des Quadrats, die 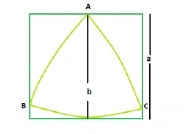a

Die Fläche des Reuleaux-Dreiecks,

A = 0,70477 * a

2

Beispiel

Input: a = 6
Output: 25.3717

Ausgabe

#include <stdio.h>
#include <math.h>
int main() {
   float a = 6;
   float area = 0.70477 * pow(a, 2);
   printf("The area is : %f",area);
   return 0;
}

Das obige ist der detaillierte Inhalt vonIn C das größte Reuleaux-Dreieck innerhalb eines Quadrats. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!