Heim >Backend-Entwicklung >C++ >Wie groß ist die Fläche des Quadrats, das durch wiederholtes Zusammenfügen der Mittelpunkte entsteht?
Wie groß ist die Fläche des Quadrats, das durch wiederholtes Zusammenfügen der Mittelpunkte entsteht?
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-09-03 22:21:101466Durchsuche
Die Fläche eines Quadrats ist gleich dem Produkt der Seitenlängen des Quadrats.
Wir betrachten eine Figur, bei der der Mittelpunkt der Seiten jedes Quadrats ein weiteres Quadrat bildet. Und so weiter, bis eine bestimmte Anzahl von Quadraten erreicht ist.
Diese Grafik zeigt ein Quadrat, das durch die Verbindung der Mittelpunkte der Quadrate entsteht.
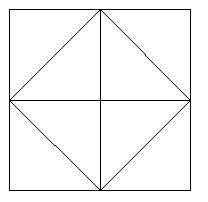
Für diese Figur sei die Seitenlänge a,
Die Seitenlänge des inneren Quadrats ist
L2 = (a/2)<sup>2</sup> + (a/2)<sup>2</sup>
L2 = a<sup>2</sup>(1/4 + 1/4) = a<sup>2</sup>(1/2) = a<sup>2</sup>/2
L = a<sup>2</sup>/ (\sqrt{2}).Die Fläche des Quadrats 2 = L2 = a2/2.
Für das nächste Quadrat, Quadrat 3 Fläche von = a2/4
Nehmen wir ein Beispiel, tge
Jetzt können wir von hier aus auf die Fläche kontinuierlicher Quadrate schließen,
a2, a 2/2, a2 /4, a2/8, …..
Dies ist eine geometrische Folge mit einem gemeinsamen Verhältnis von ½, wobei a2 der erste Term ist.
Beispiel
#include <stdio.h>
#include <math.h>
int main() {
double L = 2, n = 10;
double firstTerm = L * L;
double ratio = 1 / 2.0;
double are = firstTerm * (pow(ratio, 10)) ;
printf("The area of %lfth square is %lf", n , sum);
return 0;
}Ausgabe
The area of 10th square is 0.003906
Das obige ist der detaillierte Inhalt vonWie groß ist die Fläche des Quadrats, das durch wiederholtes Zusammenfügen der Mittelpunkte entsteht?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

