Überprüft, ob ein Diagramm, das aus einem Array basierend auf einer bestimmten Bedingung erstellt wurde, einen Zyklus enthält

Einführung

In der Graphentheorie ist es eine sehr wichtige Aufgabe, herauszufinden, ob ein aus Arrays erstellter Graph, der bestimmte Bedingungen erfüllt, einen Zyklus hat. Ein Diagramm ist eine fantasievolle Möglichkeit, zu zeigen, wie Dinge miteinander verbunden sind. Es wird an vielen Orten verwendet, beispielsweise in Computernetzwerken und sozialen Netzwerken. In diesem Artikel werden die Bedingungen für die Graphkonstruktion sowie BFS- und DFS-Algorithmen erläutert und Schritt-für-Schritt-Anleitungen zur Identifizierung von Zyklen in ungerichteten Graphen bereitgestellt.

Array-Darstellung des Diagramms

Array-basierte Methoden in der Graphentheorie speichern Scheitelpunkte und Kanten in Arrays, wodurch sie einfach zu bearbeiten und in Algorithmen zu verwenden sind. Beginnend mit einem leeren Diagramm ist das Hinzufügen von Scheitelpunkten und Kanten nacheinander basierend auf den Informationen im Array die Grundlage für weitere Untersuchungen, wie z. B. die Zykluserkennung, die wichtig ist, um zu verstehen, wie das Diagramm verknüpft ist und ob es Zyklen gibt.

Diagrammkonstruktionsbedingungen

Erläuterung der gegebenen Bedingungen

• Grafiken werden aus Arrays erstellt, wobei Arrays eine Reihe von Eckpunkten und deren Verbindungen oder Kanten darstellen.

• Jedes Element des Arrays entspricht einem Scheitelpunkt im Diagramm

• Der Wert jedes Elements im Array stellt den Index des Scheitelpunkts dar, mit dem es verbunden ist (seine benachbarten Scheitelpunkte).

• Der Index des Arrays stellt den Scheitelpunkt selbst dar, und sein entsprechender Wert stellt den Scheitelpunkt dar, mit dem es verbunden ist.

Bedingungen für die Überprüfung der Diagrammkonstruktion

• Überprüfen Sie, ob das Array gültig ist und die erforderlichen Bedingungen erfüllt, bevor Sie das Diagramm erstellen.

• Stellen Sie sicher, dass das Array nicht leer ist und mindestens ein Element enthält, um den Scheitelpunkt zu erstellen.

• Stellen Sie sicher, dass das Array nur nicht negative Ganzzahlen enthält, da negative Werte oder ungültige Daten keine gültigen Scheitelpunkte oder Kanten darstellen können

• Stellen Sie sicher, dass der Array-Index im entsprechenden Bereich liegt. Sie sollten bei 0 beginnen und bis n-1 gehen, wobei n die Gesamtzahl der Eckpunkte im Diagramm ist.

• Bestätigen Sie, dass die Werte (Verbindungen) im Array ebenfalls im gültigen Bereich von 0 bis n-1 liegen, und stellen Sie sicher, dass sie vorhandenen Scheitelpunkten entsprechen

• Überprüfen Sie, ob doppelte Verbindungen oder Selbstschleifen vorhanden sind, da diese gegen die Bedingungen für ein gültiges Diagramm verstoßen

• Stellen Sie sicher, dass keine Verbindungen verloren gehen, d. h. alle Eckpunkte sind verbunden, um ein vollständiges Diagramm oder verbundene Komponenten zu bilden

DFS- und BFS-Algorithmen

• Depth First Search (DFS) wird verwendet, um die Eckpunkte und Kanten eines Diagramms zu erkunden, indem so tief wie möglich in jeden Zweig vorgedrungen wird, bevor umgedreht wird

Pseudocode

procedure DFS(graph, start_vertex, visited)
   if start_vertex is not in visited:
      mark start_vertex as visited
      process start_vertex (e.g., check for cycles)
      for each neighbor in graph[start_vertex]:
      if neighbor is not in visited:
      DFS(graph, neighbor, visited)
   end if
end procedure
    pocedure DFS_Traversal(graph)
    visited = empty set
      for each vertex in graph:
      if vertex is not in visited:
         DFS(graph, vertex, visited)
   end for
end procedure

• Breadth-First Search (BFS) ist ein Graph-Traversal-Algorithmus, der alle Eckpunkte des Graphen Schicht für Schicht durchläuft. Dies macht es zu einer großartigen Möglichkeit, Zyklen in Diagrammen zu finden

Pseudocode

procedure BFS(graph, start_vertex):
   create an empty queue Q
   create a set visited to keep track of visited vertices
   
   enqueue start_vertex into Q
   add start_vertex to visited set
   
   while Q is not empty:
      current_vertex = dequeue from Q
      for each neighbor_vertex of current_vertex:
         if neighbor_vertex is not in visited set:
            enqueue neighbor_vertex into Q
            add neighbor_vertex to visited set
      else:
         // A cycle is detected, return true
         return true
      // No cycle found, return false
      return false

Komplexität

• Zeitliche Komplexität

Die Zeitkomplexität von BFS und DFS beträgt O(V + E), wobei V die Anzahl der Eckpunkte und E die Anzahl der Kanten ist.

• Weltraumkomplexität

Die zeitliche Komplexität von BFS und DFS beträgt O(V).

Schrittweiser Zykluserkennungsprozess

Betrachten wir ein Beispiel mit einem Diagramm

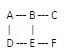
• Beginnen Sie mit einem leeren Satz, um besuchte Eckpunkte zu überwachen

Visited set: {}

• Wählen Sie einen beliebigen Scheitelpunkt als Ausgangspunkt für den Schleifenerkennungsprozess. Wir wählen Scheitelpunkt A.

Visited set: {A}
Current Vertex: A

• Überprüfen Sie die angrenzenden Scheitelpunkte des aktuellen Scheitelpunkts (A). In diesem Beispiel sind die Nachbarn von A B und D. Fügen Sie sie dem Zugriffssatz hinzu und identifizieren Sie A als seinen übergeordneten Knoten

Visited set: {A, B, D}
Current Vertex: A
Parent of B: A
Parent of D: A

• B ist der nächste besuchte Scheitelpunkt in der besuchten Menge.

Visited set: {A, B, D}
Current Vertex: B
Parent of B: A

• Erkunden Sie die Umgebung von B. Die unmittelbaren Nachbarn von B sind A, C und E. A befindet sich bereits in der besuchten Scheitelpunktmenge, ist jedoch nicht das übergeordnete Element von B und bildet daher keinen Zyklus.

Visited set: {A, B, D, C, E}
Current Vertex: B

• Fahren Sie mit dem nächsten besuchten Scheitelpunkt fort, nämlich D.

Visited set: {A, B, D, C, E}
Current Vertex: D
Parent of D: A

• Ds Bekannten gefunden. A und E sind die nächsten Nachbarn von D. Da A bereits im Zugriffssatz enthalten und das übergeordnete Element von D ist, muss es eine Kante (D -> A) geben, die D mit seinem übergeordneten Element verbindet. Dies zeigt an, dass das Diagramm einen Zyklus enthält.

Cycle detected! There is an edge (D -> A) forming a cycle

Der Prozess endet hier, wir haben die Schleife im Diagramm mit BFS erfolgreich erkannt Das heißt (A->B->E->D->A).

Fazit

Zusammenfassend lässt sich sagen, dass es für viele Anwendungen wichtig ist, Zyklen in einem Diagramm zu finden, das aus einem Array basierend auf gegebenen Parametern erstellt wurde. Unabhängig davon, ob Sie DFS oder BFS verwenden, hilft dieser Prozess dabei, mögliche Schleifen zu finden und reale Probleme im Zusammenhang mit Netzwerken, Schaltkreisen und Beziehungen zu lösen. Eine effektive Schleifenerkennung kann die Geschwindigkeit Ihres Algorithmus erhöhen und sicherstellen, dass Ihre Daten korrekt sind.

Das obige ist der detaillierte Inhalt vonÜberprüft, ob ein Diagramm, das aus einem Array basierend auf einer bestimmten Bedingung erstellt wurde, einen Zyklus enthält. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!