Memoisierung (1D, 2D und 3D) Dynamische Programmierung in Java

Memoisierung ist eine Technik, die auf dynamischer Programmierung basiert und dazu dient, die Leistung rekursiver Algorithmen zu verbessern, indem sichergestellt wird, dass eine Methode nicht mehrmals auf demselben Satz von Eingaben ausgeführt wird, indem die Ergebnisse (in einem Array gespeichert) für die bereitgestellten Eingaben aufgezeichnet werden. Die Memoisierung kann durch einen Top-Down-Ansatz erreicht werden, der rekursive Methoden implementiert.

Lassen Sie uns diese Situation anhand eines einfachen Beispiels einer Fibonacci-Folge verstehen.

1-D-Memoisierung

Wir betrachten einen rekursiven Algorithmus mit nur einem nicht konstanten Parameter (nur der Wert eines Parameters ändert sich), daher wird diese Methode als 1-D-Memoisierung bezeichnet. Der folgende Code dient zum Finden des N-ten (alle Terme bis N) in der Fibonacci-Folge.

Beispiel

public int fibonacci(int n) {
   if (n == 0)
      return 0;
   if (n == 1)
      return 1;
   System.out.println("Calculating fibonacci number for: " + n);
   return (fibonacci(n - 1) + fibonacci(n - 2));
}

Ausgabe

Wenn wir den obigen Code mit n=5 ausführen, wird die folgende Ausgabe generiert. Der Fibonacci-Wert für

Calculating fibonacci number for: 5
Calculating fibonacci number for: 4
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2
Calculating fibonacci number for: 2
Calculating fibonacci number for: 3
Calculating fibonacci number for: 2

n=5 ist: 5

Beachten Sie, dass die Fibonacci-Zahlen für 2 und 3 mehrfach berechnet werden. Um es besser zu verstehen, zeichnen wir den obigen Rekursionsbaum für die Bedingung n=5.

Die beiden untergeordneten Elemente eines Knotens stellen die rekursiven Aufrufe dar, die er durchführt. Sie können sehen, dass F(3) und F(2) mehrmals berechnet werden, was vermieden werden kann, indem die Ergebnisse nach jedem Schritt zwischengespeichert werden.

Wir werden eine Instanzvariable memoize Set verwenden, um die Ergebnisse zwischenzuspeichern. Überprüfen Sie zunächst, ob n bereits im Memoize-Set vorhanden ist. Wenn ja, geben Sie den Wert zurück. Wenn nicht, berechnen Sie den Wert und fügen Sie ihn dem Set hinzu.

Beispiel

import java.util.HashMap;
import java.util.Map;
public class TutorialPoint {
   private Map<Integer, Integer> memoizeSet = new HashMap<>(); // O(1)
   public int fibMemoize(int input) {
      if (input == 0)
         return 0;
      if (input == 1)
         return 1;
      if (this.memoizeSet.containsKey(input)) {
         System.out.println("Getting value from computed result for " + input);
         return this.memoizeSet.get(input);
      }
      int result = fibMemoize(input - 1) + fibMemoize(input - 2);
      System.out.println("Putting result in cache for " + input);
      this.memoizeSet.put(input, result);
      return result;
   }
   public int fibonacci(int n) {
      if (n == 0)
         return 0;
      if (n == 1)
         return 1;
      System.out.println("Calculating fibonacci number for: " + n);
      return (fibonacci(n - 1) + fibonacci(n - 2));
   }
   public static void main(String[] args) {
      TutorialPoint tutorialPoint = new TutorialPoint();
      System.out.println("Fibonacci value for n=5: " + tutorialPoint.fibMemoize(5));
   }
}

Ausgabe

Wenn wir den obigen Code ausführen, wird die folgende Ausgabe generiert

Adding result in memoizeSet for 2
Adding result in memoizeSet for 3
Getting value from computed result for 2
Adding result in memoizeSet for 4
Getting value from computed result for 3
Adding result in memoizeSet for 5

Der Fibonacci-Wert für n=5 ist: 5

Wie Sie oben sehen können, sind die Fibonacci-Werte für 2 und 3 Die Urkundennummer wird nicht erneut berechnet. Hier führen wir eine HashMap ein, um die berechneten Werte zu speichern. Überprüfen Sie vor jeder Fibonacci-Berechnung, ob der Wert der Eingabe in der Sammlung berechnet wurde.

2-D-Speicherung

Im obigen Programm haben wir nur einen nicht konstanten Parameter. Im folgenden Programm nehmen wir ein Beispiel eines rekursiven Programms, das über zwei Parameter verfügt, die ihren Wert nach jedem rekursiven Aufruf ändern, und implementieren zur Optimierung eine Memoisierung der beiden nicht konstanten Parameter. Dies wird als 2D-Memoisierung bezeichnet.

Zum Beispiel: Wir werden den Standard Longest Common Subsequence (LCS) implementieren. Wenn eine Menge von Folgen gegeben ist, besteht das Problem der längsten gemeinsamen Teilfolge darin, die allen Folgen gemeinsame Teilfolge mit der größten Länge zu finden. Es gibt 2^n mögliche Kombinationen.

Beispiel

class TP {
   static int computeMax(int a, int b) {
      return (a > b) ? a : b;
   }
   static int longestComSs(String X, String Y, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (X.charAt(m - 1) == Y.charAt(n - 1))
         return 1 + longestComSs(X, Y, m - 1, n - 1);
      else
         return computeMax(longestComSs(X, Y, m, n - 1), longestComSs(X, Y, m - 1, n));
   }
   public static void main(String[] args) {
      String word_1 = "AGGTAB";
      String word_2 = "GXTXAYB";
      System.out.print("Length of LCS is " + longestComSs(word_1, word_2, word_1.length(),word_2.length()));
   }
}

Ausgabe

Wenn wir den obigen Code ausführen, wird die folgende Ausgabe generiert:

Length of LCS is 4

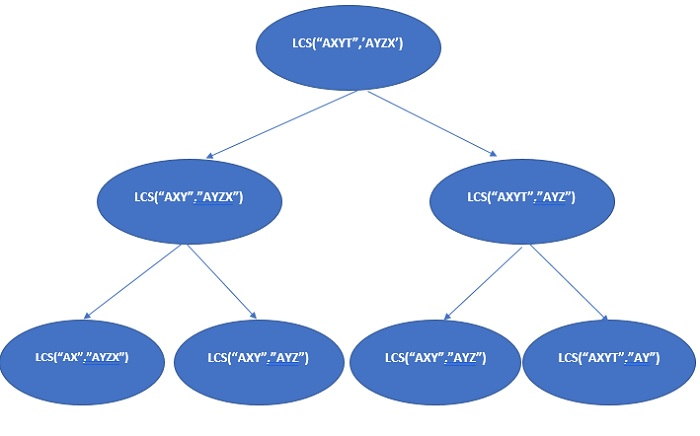
Im obigen Rekursionsbaum wird lcs("AXY", "AYZ") mehrmals gelöst.

Aufgrund der Natur dieses Problems mit überlappenden Teilstrukturen können wiederholte Berechnungen derselben Teilprobleme durch Memoisierung oder Tabellierung vermieden werden.

Die Memoisierungsmethode für rekursiven Code wird wie folgt implementiert.

Beispiel

import java.io.*;
import java.lang.*;
class testClass {
   final static int maxSize = 1000;
   public static int arr[][] = new int[maxSize][maxSize];
   public static int calculatelcs(String str_1, String str_2, int m, int n) {
      if (m == 0 || n == 0)
         return 0;
      if (arr[m - 1][n - 1] != -1)
         return arr[m - 1][n - 1];
      if (str_1.charAt(m - 1) == str_2.charAt(n - 1)) {
         arr[m - 1][n - 1] = 1 + calculatelcs(str_1, str_2, m - 1, n - 1);
         return arr[m - 1][n - 1];
      }
      else {
         int a = calculatelcs(str_1, str_2, m, n - 1);
         int b = calculatelcs(str_1, str_2, m - 1, n);
         int max = (a > b) ? a : b;
         arr[m - 1][n - 1] = max;
         return arr[m - 1][n - 1];
      }
   }
   public static void main(String[] args) {
      for (int i = 0; i < 1000; i++) {
         for (int j = 0; j < 1000; j++) {
            arr[i][j] = -1;
         }
      }
      String str_1 = "AGGTAB";
      String str_2 = "GXTXAYB";
      System.out.println("Length of LCS is " + calculatelcs(str_1, str_2, str_1.length(),str_2.length()));
   }
}

Ausgabe

Wenn wir den obigen Code ausführen, wird die folgende Ausgabe generiert:

Length of LCS is 4

Methode

Beobachtet, dass die Methode (calculatelcs) 4 Parameter enthält, von denen es 2 Konstanten gibt (nicht). beeinflussen das Auswendiglernen) und es gibt zwei nicht konstante Parameter (m und n), deren Werte sich jedes Mal ändern, wenn die Methode rekursiv aufgerufen wird. Um eine Memoisierung zu erreichen, führen wir ein zweidimensionales Array ein, um den berechneten Wert von lcs(m,n) zu speichern, der in arr[m-1][n-1] gespeichert wird. Beim erneuten Aufruf der Funktion mit den gleichen Parametern m und n führen wir keinen rekursiven Aufruf mehr durch, sondern geben direkt arr[m-1][n-1] zurück, da der zuvor berechnete lcs(m, n) gespeichert wurde arr [m-1][n-1], wodurch die Anzahl der rekursiven Aufrufe reduziert wird.

Dreidimensionale Memoisierung

Dies ist eine Memoisierungsmethode für rekursive Programme mit 3 nicht konstanten Parametern. Hier nehmen wir als Beispiel die Berechnung der LCS-Länge von drei Strings.

Der Ansatz hier besteht darin, alle möglichen Teilsequenzen einer bestimmten Zeichenfolge zu generieren (es gibt insgesamt 3ⁿ mögliche Teilsequenzen) und die längste gemeinsame Teilsequenz unter ihnen abzugleichen.

Wir werden eine dreidimensionale Tabelle zum Speichern der berechneten Werte einführen. Betrachten Sie Teilsequenzen.

• A1[1...i] i

• A2[1...j] j

Wenn wir ein gemeinsames Zeichen finden (X[i]==Y[j]==Z[k]), müssen wir die verbleibenden Zeichen rekursiv verarbeiten. Andernfalls berechnen wir den Maximalwert der folgenden Fälle:
Behalten Sie X[i] bei, um andere Zeichen rekursiv zu verarbeiten.

Behalten Sie Y[j] bei, um andere Zeichen rekursiv zu verarbeiten andere Zeichen rekursiv verarbeiten
Wenn wir also die obige Idee in eine rekursive Funktion umwandeln, dann ist

• f(N,M,K)={1+f(N-1,M-1,K-1) if (X[N] ==Y[M]==Z[K]maximum(f(N-1,M,K),f(N,M-1,K),f(N,M,K- 1))}

• f(N-1,M,K) = Reserviere X[i], um andere Zeichen rekursiv zu verarbeiten

f(N,M-1,K) = Reserviere Y[j] für Andere Zeichen rekursiv verarbeiten

f(N,M,K-1) = Z[k] beibehalten, um andere Zeichen rekursiv zu verarbeiten
Beispiel

• import java.io.IOException;
  import java.io.InputStream;
  import java.util.*;
  class testClass {
     public static int[][][] arr = new int[100][100][100];
     static int calculatelcs(String str_1, String str_2, String str_3, int m, int n, int o) {
           for (int i = 0; i <= m; i++) {
              for (int j = 0; j <= n; j++) {
                 arr[i][j][0] = 0;
              }
           }
           for (int i = 0; i <= n; i++) {
              for (int j = 0; j <= o; j++) {
                 arr[0][i][j] = 0;
              }
           }
           for (int i = 0; i <= m; i++) {
              for (int j = 0; j <= o; j++) {
                 arr[i][0][j] = 0;
              }
           }
           for (int i = 1; i <= m; i++) {
              for (int j = 1; j <= n; j++) {
                 for (int k = 1; k <= o; k++) {
                    if (str_1.charAt(i - 1) == str_2.charAt(j-1) && str_2.charAt(j1) == str_3.charAt(k-1)) {
                       arr[i][j][k] = 1 + arr[i - 1][j - 1][k - 1];
                    }
                    else {
                       arr[i][j][k] = calculateMax(arr[i - 1][j][k], arr[i][j - 1][k], arr[i][j][k - 1]);
                    }
                 }
              }
           }
           return arr[m][n][o];
     }
     static int calculateMax(int a, int b, int c) {
        if (a > b && a > c)
           return a;
           if (b > c)
           return b;
           return c;
     }
     public static void main(String[] args) {
        String str_1 = "clued";
        String str_2 = "clueless";
        String str_3 = "xcxclueing";
        int m = str_1.length();
        int n = str_2.length();
        int o = str_3.length();
        System.out.print("Length of LCS is " + calculatelcs(str_1, str_2, str_3, m, n, o));
     }
  }

  Ausgabe

Wenn wir den obigen Code ausführen, wird die folgende Ausgabe ausgegeben wird generiert

• Length of LCS is 4

Das obige ist der detaillierte Inhalt vonMemoisierung (1D, 2D und 3D) Dynamische Programmierung in Java. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!