Ich habe mir heimlich ein paar Computer-Grundlagen angesehen und von nun an ist das Erlernen von Java wie Betrug!

Bevor ich Java lerne, möchte ich eine Frage stellen: Halten Sie es für notwendig, Computergrundlagen zu erlernen?

Viele Leute denken, dass es nicht nötig ist, diese langweiligen und obskuren Grundkenntnisse zu lesen. Es ist besser, direkt mit HelloWorld zu beginnen, sich einen Eindruck zu verschaffen, und der Code wird ausgeführt, und dann wird nach und nach die Syntax erlernt Lesen Sie das Programm eingehend und verwenden Sie es schließlich zum Erstellen des Projekts. Das ist die praktische Lernmethode.

Zuallererst leugne ich nicht, dass diese Art des Lernens für einige Studenten besser geeignet ist, insbesondere für diejenigen, die darauf bedacht sind, zuerst einen Job zu finden Später im Detail verstehen: Nichts ist wichtiger als Brot?

Aber unseren Schülern, die Logarithmen von Grund auf lernen, empfehle ich dennoch, mit einigen Grundkenntnissen über Computer zu beginnen, um die Ideen und den gesunden Menschenverstand der Programmierung zu verstehen, was auch für unser zukünftiges Studium sehr hilfreich sein wird. Es ist, als würde man ein Haus bauen. Manche Leute bauen Strohhäuser, manche bauen Lehmhäuser und manche wollen ein zweistöckiges Haus im westlichen Stil bauen. Die Tiefe des Fundaments bestimmt direkt das Niveau der zukünftigen Erfolge.

Lassen Sie uns nun kurz einige Grundkenntnisse über Computer verstehen.

1. Klassifizierung der Maschinensprache

Maschinensprache

Maschinensprache ist eine Sprache, die von Computern direkt erkannt werden kann. Es handelt sich um eine Computersprache, die direkt in Binärcodeanweisungen ausgedrückt wird. Es handelt sich um einen Code, der aus einer Folge von Nullen und Einsen mit einer bestimmten Anzahl von Ziffern besteht und in mehrere Segmente unterteilt ist. Die Codierung jedes Segments hat eine andere Bedeutung. Das Folgende ist beispielsweise eine einfache Zeichenfolge von Maschinencodes:

010100100000  // 520

So viele Leute fragen sich, warum der Maschinencode aus 0 und 1 besteht?

Da der Maschinencode die Computerhardware steuern muss, um auf die Programmanweisungen zu reagieren, stellt 0 ein niedriges Potenzial und 1 ein hohes Potenzial dar, sodass eine Logikschaltung erzeugt werden kann, die der Steuerung eines Schalters 0 entspricht 1 ist offen.

Assemblersprache

Assemblersprache ist eine Sprache für Entwickler. Da die Maschinensprache nur aus 0 und 1 besteht, ist es für Entwickler schwierig, sie direkt zu steuern und zu verwenden. Daher müssen einige spezielle Symbole als Markierungen für Binärcodes verwendet werden . Entwickler schließen die Befehlsausgabe ab, indem sie diese speziellen Symbole eingeben und den Computer für uns arbeiten lassen. Computer können Assemblersprache nicht direkt erkennen, und es ist eine Software erforderlich, um Assemblersprache in Maschinensprache zu übersetzen. Der Unterschied zur Maschinensprache liegt in der Darstellungsmethode der Anweisungen. Der Hauptteil der Assemblersprache sind Assembleranweisungen, die sich Programmierer leichter merken können.

MOV AX,1234H  //汇编指令: 寄存器AX的内容送到1234H中
101110000011010000010010 //机器指令

Hochsprachen

Gemeinsame Hochsprachen sind: C, C++, Java, Python, PHP usw.

Es kommt unserem normalen menschlichen Denken näher. Sein größtes Merkmal ist, dass es einfach zu schreiben und der Code lesbar ist. Um die gleiche Funktion zu erreichen, ist die Verwendung von Hochsprachen kürzer, der Programmcode kürzer und einfacher zu lesen. Zweitens sind Hochsprachen portierbar, das heißt, ein Code kann ohne oder mit nur geringen Änderungen auf verschiedenen Computertypen ausgeführt werden.

print('Hello World')   // python版HelloWorld

我们从这个程序可以看出来，高级语言屏蔽了机器内部指令运行细节，我们可以像写作一样书写程序，而不用关心语言内部的实现细节，这大大提高了我们的开发效率，节约开发成本。

当然，其缺点也很明显，使用高级语言编写的程序运行时，需要先将其翻译成低级语言计算机才能运行它，在翻译过程中可能会产生一些多余的部分，运行效率低些。另外，对硬件的可控性相对于低级语言弱些，目标代码量较大。

二. 进制

推荐使用在线工具进行进制转换：

https://tool.oschina.net/hexconvert/

二进制

由数字0和1组成，逢二进一，比如机器码就是二进制的，是最简单的计算机可读懂的代码，例如 0101（表示十进制数字5）。

八进制

由1到7组成的数字串，数字最大不会超过7，逢八进一，例如 157(表示十进制数字111)

十进制

我们日常使用的数字都是十进制类型的，逢十进一，例如  0123456789。

十六进制

由1到9，a-f（或者是A-F，分别代表10-15）组成的数字串，数字最大不会超过15，其中字母是不区分大小写的，逢十六进一，例如0F83（表示十进制数3971）

进制转换

1. K进制与十进制数的转换

假设有一个n+1位的K进制数，它的形式如下：

AnAn-1…A3A2A1A0
则它的大小为：（也就是对应的我们能看懂的十进制数为）

A0 * K^0 + A1 * K^1....+ An * K^n      //K^n表示K的n次方

二进制数：10101 转换成 十进制数为：21

 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1+1*2^0 = 21

2. 十进制与k进制的转换

短除法。

举个栗子：

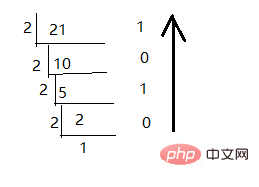
从图可以看出，用十进制数21一直除以2，每次得到的余数倒数就是最后的二进制数10101。同样，十进制转八进制、十进制转十六进制都是一样的套路，非常简单。

3. 二进制与八进制和十六进制之间转换

8是2的3次方，16是2的4次方，所以这之间的转换存在一种快捷方法。以2转8示例，将2进制从低位到高位，每3个一组，如果是十六进制就每4个一组，高位不足3位的补0，然后将每组依次转换成对应的十进制，得到的结果就是对应的8进制或者16进制。

二进制10101100101转八进制：2545

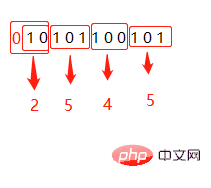
二进制10101100101转十六进制：565

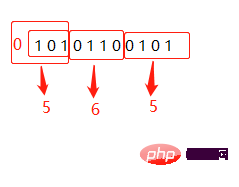
三. 原码、反码、补码

在计算机中，最小的单位是位，也称为比特（bit）。而另一个常用单位是字节，一个字节是8位，也就是8比特，所以我们常用的二进制表示法是8位。

原码

原码是一种非常常见的二进制表示形式。在原码中，为了区别正数和负数，将二进制中的最高位作为符号位，如果是0表示正数，如果是1表示负数。

举个栗子：

0000 0001   // 表示 1
1000 0001   // 表示 -1

反码

不知道大家有没有注意到原码的一个问题，那就是负数参与计算的时候，比如

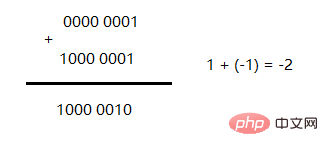
出现了一个大问题，就是1 + (-1) 不等于0，而等于 -2。

这可咋整？

Um dieses Problem zu lösen, haben die Vorgänger intelligenter Computer den Inversionscode entwickelt. Die Regel zum Konvertieren des Originalcodes in den Umkehrcode lautet: Der Umkehrcode einer positiven Zahl ist er selbst, der Umkehrcode einer negativen Zahl besteht darin, dass das Vorzeichenbit unverändert bleibt und die anderen Bits invertiert werden. Die Negationsregel lautet: Wenn es 0 ist, wird es zu 1, und wenn es 1 ist, wird es zu 0.
Werfen wir einen Blick auf die Berechnung der Konvertierung in den Umkehrcode:

Das Ergebnis ist 1111 1111.

Hey? Das stimmt nicht, warum ist es nicht 0?

Keine Sorge, dies ist nur das Berechnungsergebnis des inversen Codes. Wir konvertieren den inversen Code in den ursprünglichen Code 1111 1111 –> und erhalten -0, was 0 entspricht das erwartete Ergebnis und löst auch die Berechnung der ursprünglichen Codefrage.

Komplementärer Code

Inverser Code löst das Problem der Berechnung negativer Zahlen, aber es gibt noch ein Problem, das noch nicht gelöst wurde, nämlich -0 . Aufgrund des Vorzeichenbits des höchsten Bits einer negativen Zahl kann die ursprüngliche 8-Bit-Binärzahl 2 hoch 8 darstellen, d. h. 256 Zahlen können jedoch nur verwendet werden stellen 255 dar, was für uns sehr unangenehm ist. Wie können wir diese fehlende Zahl ausgleichen?

Die kahlköpfigen Programmierer haben auch die entsprechende Lösung gefunden – Code-Ergänzung.

Regeln zum Konvertieren des Originalcodes in Komplementcode: Der Komplementcode einer positiven Zahl ist er selbst, der Komplementcode einer negativen Zahl besteht darin, dass das Vorzeichenbit unverändert bleibt und die verbleibenden Ziffern invertiert werden (d. h. zum Komplementcode werden). ) und addiere 1.

Zum Beispiel:

Originalcode: 0000 0001, Komplementcode: 0000 0001
Originalcode: 1000 0001, Komplementcode: 1111 1111

Berechnen Sie:

Wie aus dem ersichtlich ist oben verwenden Sie die Komplementcode Die Berechnung ergibt 0 (anstelle von -0) und löst das Problem einer Zahl weniger.

Im Komplementcode wird angegeben, dass 0 als 0000 0000 und 1000 0000 als -128 dargestellt wird. Beachten Sie, dass dies eine Regel ist.

Hinweise

1. Einerkomplement und Einerkomplement können nicht direkt in die entsprechende Dezimalzahl umgewandelt werden, um die entsprechende Größe zu erhalten. Mit anderen Worten, der Originalcode ist eine Ausdrucksform, die in direktem Zusammenhang mit der Größe steht

2. In Computersystemen werden Werte immer in Form von Komplementärcodes ausgedrückt und gespeichert

3. Der ursprüngliche Code, das Komplement und das Komplement positiver Zahlen sind gleich.

4. Negative Zahlen werden umgekehrt: Das Vorzeichenbit bleibt unverändert, und die verbleibenden Bits werden invertiert.

5. Negative Zahlen werden umgekehrt: Das Vorzeichenbit bleibt gleich unverändert, Negative Zahlen werden invertiert, nachdem die verbleibenden Bits invertiert und eins hinzugefügt wurden.

6. Negative Zahlen werden invertiert: Das Vorzeichenbit bleibt unverändert und die verbleibenden Bits werden um eins reduziert. Negative Zahlen werden invertiert: Das Vorzeichenbit bleibt unverändert und die restlichen Bits werden um eins reduziert und invertiert

Das obige ist der detaillierte Inhalt vonIch habe mir heimlich ein paar Computer-Grundlagen angesehen und von nun an ist das Erlernen von Java wie Betrug!. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!