Heim >Java >javaLernprogramm >Benutze es jeden Tag! Wissen Sie, was HASH ist?
Benutze es jeden Tag! Wissen Sie, was HASH ist?
- Java学习指南nach vorne
- 2023-07-26 14:47:45720Durchsuche
Haben Sie jemals HashMap verwendet? Haben Sie also ernsthaft verstanden, was Hash ist? Dieser Artikel führt Sie durch eine detaillierte Untersuchung des Hash-Algorithmus auf grundsätzlicher Ebene.
1. Das Konzept des Hashing
Die Hauptidee der Hashing-Methode besteht darin, die Speicheradresse basierend auf dem Schlüsselcodewert des Knotens zu bestimmen: Nehmen Sie den Schlüsselcodewert K als unabhängige Variable durch Berechnen Sie eine bestimmte funktionale Beziehung h(K) (sogenannte Hash-Funktion), berechnen Sie den entsprechenden Funktionswert, interpretieren Sie diesen Wert als Speicheradresse des Knotens und speichern Sie den Knoten in dieser Speichereinheit. Verwenden Sie beim Abrufen dieselbe Methode, um die Adresse zu berechnen, und gehen Sie dann zur entsprechenden Einheit, um den gesuchten Knoten zu erhalten. Knoten können durch Hashing schnell abgerufen werden. Hash (auch „Hash“ genannt) ist eine wichtige Speichermethode und eine gängige Abrufmethode.
Die gemäß der Hash-Speichermethode erstellte Speicherstruktur wird als Hash-Tabelle bezeichnet. Eine Position in der Hash-Tabelle wird als Slot bezeichnet. Der Kern der Hashing-Technologie ist die Hash-Funktion. Wenn für jede gegebene dynamische Nachschlagetabelle DL eine „ideale“ Hash-Funktion h und die entsprechende Hash-Tabelle HT ausgewählt werden, dann für jedes Datenelement X in DL. Der Funktionswert h (X.key) ist der Speicherort von X in der Hash-Tabelle HT. Das Datenelement X wird beim Einfügen (oder Erstellen einer Tabelle) an dieser Position platziert und beim Abrufen von X auch an dieser Position gesucht. Der durch die Hash-Funktion ermittelte Speicherort wird Hash-Adresse genannt. Daher besteht der Kern des Hashings darin, dass die Hash-Funktion die entsprechende Beziehung zwischen dem Schlüsselcodewert (X.key) und der Hash-Adresse h (X.key) bestimmt. Durch diese Beziehung werden organisatorische Speicherung und Abruf realisiert.
Im Allgemeinen ist der Speicherplatz der Hash-Tabelle ein eindimensionales Array HT[M], und die Hash-Adresse ist der Index des Arrays. Das Ziel beim Entwerfen einer Hashing-Methode besteht darin, eine bestimmte Hash-Funktion h, 0<=h(K) In der folgenden Diskussion gehen wir davon aus, dass es sich um Schlüsselcodes handelt, deren Werte ganze Zahlen sind. Ansonsten können wir immer eine Eins-zu-eins-Entsprechung zwischen Schlüsselcodes und positiven ganzen Zahlen herstellen. Damit der Abruf des Schlüssels gleichzeitig in einen Abruf der entsprechenden positiven Ganzzahl umgewandelt wird, wird weiterhin angenommen, dass der Wert der Hash-Funktion zwischen 0 und M-1 liegt. Die Grundsätze für die Auswahl einer Hash-Funktion sind: Die Operation muss so einfach wie möglich sein. Der Wertebereich der Funktion muss so gleichmäßig wie möglich innerhalb des Gültigkeitsbereichs der Hash-Tabelle liegen Verschiedene Schlüssel haben unterschiedliche Hash-Funktionswerte. Dabei müssen verschiedene Faktoren berücksichtigt werden: Schlüssellänge, Hash-Tabellengröße, Schlüsselverteilung, Häufigkeit des Datensatzabrufs usw. Im Folgenden stellen wir einige häufig verwendete Hash-Funktionen vor. Wie der Name schon sagt, besteht die Divisionsmethode darin, den Schlüsselcode x durch M zu dividieren (häufig wird die Länge der Hash-Tabelle verwendet) und der Rest als Hash-Adresse verwendet. Die Restmethode ist fast die einfachste Hashing-Methode und die Hash-Funktion lautet: h(x) = x mod M. Wenn Sie diese Methode verwenden, multiplizieren Sie zunächst den Schlüsselcode mit einer Konstanten A (0< A < 1) und extrahieren Sie den Dezimalteil des Produkts. Anschließend multiplizieren Sie diesen Wert mit der Ganzzahl n, runden das Ergebnis ab und verwenden es als Hash-Adresse. Die Hash-Funktion lautet: Hash (Schlüssel) = _LOW(n × (A × Schlüssel % 1)). Unter diesen bedeutet „A × Schlüssel % 1“, dass der Dezimalteil von A × Schlüssel genommen wird, das heißt: A × Schlüssel % 1 = A × Schlüssel - _LOW(A × Schlüssel), und _LOW(X) bedeutet, den ganzzahligen Teil zu nehmen von Die spezifische Implementierung der Quadrat-Mittel-Methode besteht darin, zunächst den Quadratwert des Schlüsselcodes zu ermitteln, um die Differenz zwischen ähnlichen Zahlen zu erweitern, und dann die mittleren Ziffern (häufig Binärbits) entsprechend der Länge der Tabelle als Hash-Funktion zu verwenden Wert. Da die mittleren Ziffern eines Produkts mit jeder Ziffer des Multiplikators verknüpft sind, ist die resultierende Hash-Adresse einheitlicher. Zum Beispiel: Erstellen einer Hash-Tabelle mit der Anzahl der Datenelemente n=80 und der Hash-Länge m=100. Ohne Beschränkung der Allgemeinheit geben wir hier nur 8 Schlüsselwörter zur Analyse an. Die 8 Schlüsselwörter lauten wie folgt: K1=61317602 K2=61326875 K3=62739628 K4=61343634 K5=62706815 K6=62774638 K7=61381262 K8 =61394220 Die Analyse der oben genannten 8 Schlüsselwörter zeigt, dass die Werte der 1., 2., 3. und 6. Ziffer von links nach rechts des Schlüsselworts relativ konzentriert sind und nicht als Hash-Adressen geeignet sind. Die restlichen 4., 5., 7. Die 8-Bit-Werte sind relativ gleichmäßig und zwei davon können als Hash-Adresse ausgewählt werden. Angenommen, die letzten beiden Ziffern werden als Hash-Adresse ausgewählt, dann lauten die Hash-Adressen dieser acht Schlüsselwörter: 2, 75, 28, 34, 15, 38, 62, 20. Diese Methode eignet sich für: die Häufigkeit des Auftretens verschiedener Zahlen in jeder Ziffer aller Schlüsselwörter im Voraus abschätzen zu können. Behandeln Sie den Schlüsselwert als Zahl in einer anderen Basis, konvertieren Sie ihn dann in die ursprüngliche Zahl und wählen Sie dann einige davon als Hash-Adresse aus. Beispiel Hash(80127429)=(80127429)13=8137+0136+1135+2134+7133+4132+2*131+9=(502432641)10 Wenn Sie die mittleren drei Ziffern als Hashwert nehmen, erhalten Sie Hash (80127429) =432
Um eine gute Hash-Funktion zu erhalten, können mehrere Methoden kombiniert werden, z. B. zuerst die Basis ändern, dann falten oder quadrieren usw. Solange der Hash einheitlich ist, können Sie ihn nach Belieben zusammensetzen. Manchmal enthält der Schlüsselcode viele Ziffern und es ist zu kompliziert, die Quadratmethode zur Berechnung zu verwenden. Dann kann der Schlüsselcode in mehrere Teile mit der gleichen Anzahl von Ziffern unterteilt werden ( Die Anzahl der Ziffern im letzten Teil kann unterschiedlich sein. Anschließend wird die Überlagerungssumme dieser Teile (ohne Übertrag) als Hash-Adresse verwendet. Diese Methode wird Faltmethode genannt. ist unterteilt in: Obwohl das Ziel der Hash-Funktion darin besteht, Konflikte zu minimieren, sind Konflikte tatsächlich unvermeidbar. Daher müssen wir uns mit Konfliktlösungsstrategien befassen. Konfliktlösungstechniken können in zwei Kategorien unterteilt werden: offenes Hashing (auch bekannt als Zipper-Methode, separate Verkettung) und geschlossenes Hashing-Verfahren (geschlossenes Hashing, auch bekannt als offene Adressmethode, offene Adressierung). Der Unterschied zwischen diesen beiden Methoden besteht darin, dass die offene Hashing-Methode den kollidierenden Schlüssel außerhalb der Haupt-Hash-Tabelle speichert, während die geschlossene Hashing-Methode den kollidierenden Schlüssel in einem anderen Slot in der Tabelle speichert. (1) Zipper-Methode Eine einfache Form der Hash-Methode besteht darin, jeden Slot in der Hash-Tabelle als Kopf einer verknüpften Liste zu definieren. Alle Datensätze, die zu einem bestimmten Slot gehasht werden, werden in die verknüpfte Liste für diesen Slot aufgenommen. Abbildung 9-5 zeigt eine offene Hash-Tabelle, in der jeder Slot einen Datensatz und einen Zeiger auf den Rest der verknüpften Liste speichert. Diese 7 Zahlen werden in einer Hash-Tabelle mit 11 Slots gespeichert und die verwendete Hash-Funktion ist h(K) = K mod 11. Die Einfügungsreihenfolge der Zahlen ist 77, 7, 110, 95, 14, 75 und 62. Es gibt 2 gehaschte Werte für Slot 0, 1 gehashten Wert für Slot 3, 3 gehaschte Werte für Slot 7 und 1 gehashten Wert für Slot 9. Die geschlossene Hashing-Methode speichert alle Datensätze direkt in der Hash-Tabelle. Jeder Datensatzschlüssel hat eine Basisposition, die durch eine Hash-Funktion berechnet wird, nämlich h(Schlüssel). Wenn ein Schlüssel eingefügt werden soll und ein anderer Datensatz bereits die Basisposition von R einnimmt (es kommt zu einer Kollision), wird R an einer anderen Adresse in der Tabelle gespeichert und die Konfliktlösungsrichtlinie bestimmt, um welche Adresse es sich handelt. Die Grundidee der Konfliktlösung in geschlossenen Hash-Tabellen ist: Wenn ein Konflikt auftritt, verwenden Sie eine bestimmte Methode, um eine Hash-Adresssequenz d0, d1, d2, ... di, ... dm-1 für Schlüssel K zu generieren . Unter diesen wird d0=h (K) als Basisadressen-Heimatposition von K bezeichnet; alle di (0< i< m) sind nachfolgende Hash-Adressen. Wenn beim Einfügen von K der Knoten an der Basisadresse bereits durch andere Datenelemente belegt ist, wird er der Reihe nach gemäß der obigen Adresssequenz abgetastet und die erste gefundene offene freie Position di wird als Speicherort von K verwendet ; wenn alle nachfolgenden Hashes keine Adressen frei haben, was darauf hinweist, dass die geschlossene Hash-Tabelle voll ist und ein Überlauf gemeldet wird. Dementsprechend wird beim Abrufen von K die Folge von Nachfolgeradressen mit demselben Wert nacheinander durchsucht und die Position di zurückgegeben, wenn beim Abrufen entlang der Sondierungssequenz eine offene freie Adresse gefunden wird dass im Tabellencode kein zu durchsuchender Schlüssel vorhanden ist. Beim Löschen von K suchen wir auch sequentiell nach der Reihenfolge der Nachfolgeradressen mit demselben Wert. Wenn wir feststellen, dass eine bestimmte Position di den K-Wert hat, löschen wir das Datenelement an der Position di (der Löschvorgang markiert tatsächlich nur die). Knoten zum Löschen); Wenn eine offene freie Adresse gefunden wird, bedeutet dies, dass in der Tabelle kein zu löschender Schlüssel vorhanden ist. Daher ist für geschlossene Hash-Tabellen die Methode zum Erstellen einer Folge aufeinanderfolgender Hash-Adressen die Methode zum Umgang mit Konflikten. Unterschiedliche Methoden der Sondenbildung führen zu unterschiedlichen Methoden der Konfliktlösung. Nachfolgend sind einige gängige Baumethoden aufgeführt. (1) Die lineare Erkennungsmethode betrachtet die Hash-Tabelle als Ringtabelle. Wenn an der Basisadresse d (d. h. h(K)=d) ein Konflikt auftritt, werden die folgenden Adresseinheiten nacheinander geprüft: d +1 , d+2,...,M-1,0,1,...,d-1 bis eine freie Adresse oder ein Knoten mit dem Schlüsselcode gefunden wird. Wenn Sie nach der Suche entlang der Sondierungssequenz zur Adresse d zurückkehren, bedeutet dies natürlich einen Fehler, unabhängig davon, ob Sie eine Einfügeoperation oder eine Abrufoperation durchführen. Die Sondenfunktion für eine einfache lineare Sonde lautet: p(K,i) = i Beispiel 9.7 Es ist bekannt, dass eine Reihe von Schlüsselcodes (26, 36, 41, 38, 44, 15, 68, 12, 06, 51, 25) ist, die Länge der Hash-Tabelle M = 15, linear verwenden Explorationsmethode zum Lösen von Konflikten und zum Erstellen dieser festgelegten Hash-Schlüsseltabelle. Da n = 11, verwenden Sie die Restmethode, um eine Hash-Funktion zu erstellen und die größte Primzahl P = 13 kleiner als M auszuwählen. Dann lautet die Hash-Funktion: h(key) = key%13. Fügen Sie jeden Knoten in der Reihenfolge ein: 26: h(26) = 0, 36: h(36) = 10, 41: h(41) = 2, 38: h(38) = 12, 44: h(44) = 5 . Wenn 15 eingefügt wird, ist seine Hash-Adresse 2. Da 2 bereits durch das Element mit dem Schlüsselcode 41 belegt ist, muss es geprüft werden. Gemäß der sequentiellen Prüfmethode ist 3 offensichtlich eine offene freie Adresse und kann daher in Einheit 3 platziert werden. Ebenso können 68 und 12 in den Einheiten 4 bzw. 13 platziert werden. (2) Quadratische Sondierungsmethode Die Grundidee der quadratischen Sondierungsmethode ist: Die generierten nachfolgenden Hash-Adressen sind nicht kontinuierlich, sondern gesprungen um Platz für nachfolgende Datenelemente zu lassen, um die Aggregation zu reduzieren. Die Erkennungssequenz der sekundären Erkennungsmethode lautet: 12, -12, 22, -22 usw. Das heißt, wenn ein Konflikt auftritt, werden die Synonyme an beiden Enden der ersten Adresse hin und her gehasht. Die Formel zum Finden der nächsten offenen Adresse lautet: (3) Zufällige Sondierungsmethode Die ideale Sondierungsfunktion sollte zufällig die nächste Position aus einem nicht besuchten Slot in der Sondierungssequenz auswählen. Das heißt, Die Sondensequenz sollte eine zufällige Permutation der Hash-Tabellenpositionen sein. Wir können jedoch nicht zufällig eine Position aus der Sondensequenz auswählen, da beim Abrufen des Schlüssels nicht dieselbe Sondensequenz ermittelt werden kann. Wir können jedoch so etwas wie eine pseudozufällige Untersuchung durchführen. Bei der pseudozufälligen Sondierung ist der i-te Slot in der Sondierungssequenz (h(K) + ri) mod M, wobei ri eine „zufällige“ Folge von Zahlen zwischen 1 und M – 1 ist. Alle Einfügungen und Abrufe verwenden dieselbe „zufällige“ Zahl. Die Sondenfunktion lautet p(K,i) = perm[i – 1], wobei perm ein Array der Länge M – 1 ist, das eine zufällige Folge von Werten von 1 bis M – 1 enthält. Beispiel: Zum Beispiel ist die bekannte Hash-Tabellenlänge m = 11, die Hash-Funktion lautet: H (Schlüssel) = Schlüssel % 11, dann H (47) = 3, H (26) = 4, H (60 )=5, vorausgesetzt, das nächste Schlüsselwort ist 69, dann ist H(69)=3, was mit 47 in Konflikt steht. Wenn lineare Erkennung und anschließendes Hashing verwendet werden, um Konflikte zu behandeln, ist die nächste Hash-Adresse H1=(3 + 1) % 11 = 4. Wenn immer noch ein Konflikt besteht, ist die nächste Hash-Adresse H2 = (3 + 2) % 11 = 5. , es gibt immer noch einen Konflikt, suchen Sie weiterhin die nächste Hash-Adresse als H3 = (3 + 3)% 11 = 6, es gibt zu diesem Zeitpunkt keinen Konflikt mehr, füllen Sie 69 in Einheit 5, siehe Abbildung 8.26 (a ). Wenn Sie sekundäre Erkennung und Hashing verwenden, um Konflikte zu behandeln, ist die nächste Hash-Adresse H1 = (3 + 12) % 11 = 4. Wenn immer noch ein Konflikt besteht, suchen Sie die nächste Hash-Adresse H2 = (3 - 12) % 11 = 2. Zu diesem Zeitpunkt liegt kein Konflikt vor. Füllen Sie 69 in Einheit 2 aus, siehe Abbildung 8.26 (b). Wenn Pseudozufallserkennung und anschließendes Hashing zur Konfliktbehandlung verwendet werden und die Pseudozufallszahlenfolge 2, 5, 9,…….. lautet, lautet die nächste Hash-Adresse H1 = (3 + 2)% 11 = 5, und es gibt immer noch einen Konflikt, dann finden Sie die nächste Hash-Adresse als H2 = (3 + 5)% 11 = 8. Zu diesem Zeitpunkt liegt kein Konflikt vor, füllen Sie 69 in Einheit 8 ein, siehe Abbildung 8.26 (c). (4)Doppelte Hash-Erkennungsmethode Pseudozufälliges Prüfen und sekundäres Prüfen können das Problem der Basisaggregation beseitigen, d. h. Schlüsselcodes mit unterschiedlichen Basisadressen und bestimmte Segmente ihrer Prüfsequenzen überlappen sich. Wenn jedoch zwei Schlüssel auf dieselbe Basisadresse gehasht werden, wird mit beiden Methoden immer noch dieselbe Sondensequenz erhalten, und es findet weiterhin eine Aggregation statt. Dies liegt daran, dass die durch pseudozufällige Sondierung und sekundäre Sondierung erzeugte Sondierungssequenz nur eine Funktion der Basisadresse und nicht eine Funktion des ursprünglichen Schlüsselwerts ist. Dieses Problem wird als sekundäres Clustering bezeichnet. Um eine sekundäre Aggregation zu vermeiden, müssen wir die Sondensequenz zu einer Funktion des ursprünglichen Schlüsselwerts und nicht zu einer Funktion der Basisposition machen. Die Doppel-Hash-Erkennungsmethode verwendet die zweite Hash-Funktion als Konstante, überspringt jedes Mal den konstanten Term und führt eine lineare Erkennung durch.
2. Hash-Funktion
1. Divisionsmethode
2. Multiplikations-Restrundungsmethode
4. Numerische Analysemethode
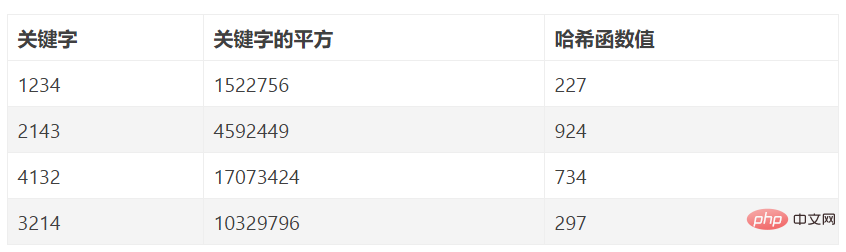 Nehmen Sie an, dass jedes Schlüsselwort im Schlüsselwortsatz aus s Ziffern (u1, u2, …, us) besteht, analysieren Sie den gesamten Schlüsselwortsatz und extrahieren Sie mehrere gleichmäßig verteilte Bits oder deren Kombination als Adressen. Bei der digitalen Analysemethode werden einige digitale Bits mit relativ einheitlichen Werten in den Schlüsselwörtern der Datenelemente als Hash-Adresse verwendet. Das heißt, wenn das Schlüsselwort viele Ziffern hat, können Sie die Bits des Schlüsselworts analysieren und die ungleichmäßig verteilten Bits als Hash-Wert verwerfen. Es ist nur geeignet, wenn alle Keyword-Werte bekannt sind. Durch die Analyse der Verteilung wird der Keyword-Wertebereich in einen kleineren Keyword-Wertebereich umgewandelt.
Nehmen Sie an, dass jedes Schlüsselwort im Schlüsselwortsatz aus s Ziffern (u1, u2, …, us) besteht, analysieren Sie den gesamten Schlüsselwortsatz und extrahieren Sie mehrere gleichmäßig verteilte Bits oder deren Kombination als Adressen. Bei der digitalen Analysemethode werden einige digitale Bits mit relativ einheitlichen Werten in den Schlüsselwörtern der Datenelemente als Hash-Adresse verwendet. Das heißt, wenn das Schlüsselwort viele Ziffern hat, können Sie die Bits des Schlüsselworts analysieren und die ungleichmäßig verteilten Bits als Hash-Wert verwerfen. Es ist nur geeignet, wenn alle Keyword-Werte bekannt sind. Durch die Analyse der Verteilung wird der Keyword-Wertebereich in einen kleineren Keyword-Wertebereich umgewandelt.
5. Basiskonvertierungsmethode
6. Faltmethode
3. Konfliktlösungsstrategie
1. Getrennte verknüpfte Listenmethode
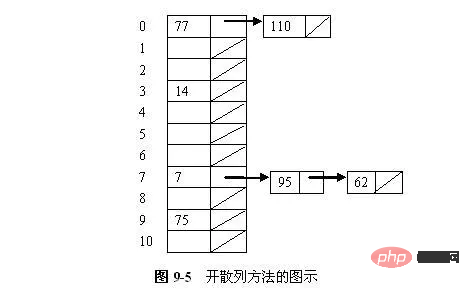
2. Geschlossene Hashing-Methode (offene Adressmethode)



Das obige ist der detaillierte Inhalt vonBenutze es jeden Tag! Wissen Sie, was HASH ist?. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!
In Verbindung stehende Artikel
Mehr sehen- Verwenden Sie die HashMap.size()-Funktion von Java, um die Größe einer HashMap zu ermitteln
- Verwenden Sie die HashMap.get()-Funktion von Java, um Elemente in einer HashMap abzurufen
- Berechnen Sie den Hash-Code eines mehrdimensionalen Arrays mit der Java-Funktion Arrays.deepHashCode()
- Verwenden Sie die HashMap.values()-Funktion von Java, um alle Werte in der HashMap abzurufen
- Verwenden Sie die HashMap.containsKey()-Funktion von Java, um zu bestimmen, ob die HashMap den angegebenen Schlüssel enthält

