Heim >Web-Frontend >H5-Tutorial >Tutorial zum Zeichnen von Bögen und Kreisen über die HTML5 Canvas API_HTML5-Tutorial-Tipps
Tutorial zum Zeichnen von Bögen und Kreisen über die HTML5 Canvas API_HTML5-Tutorial-Tipps
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOriginal
- 2016-05-16 15:45:301878Durchsuche
In HTML5 stellt das CanvasRenderingContext2D-Objekt auch Methoden speziell zum Zeichnen von Kreisen oder Bögen bereit. Bitte beachten Sie die folgenden Attribute und Methodeneinführung:
- arc(x, y, radius, startRad, endRad, gegen den Uhrzeigersinn)
Zeichnen Sie auf der Leinwand einen Bogen auf einem Kreis mit dem Koordinatenpunkt (x, y) als Mittelpunkt und dem Radius als Radius. Der Anfangsbogen dieses Bogens ist startRad und der Endbogen ist endRad. Das Bogenmaß wird hier als Winkel der Drehung im Uhrzeigersinn basierend auf der positiven Richtung der x-Achse (drei Uhr auf der Uhr) berechnet. Gegen den Uhrzeigersinn gibt an, ob mit dem Zeichnen gegen den Uhrzeigersinn oder im Uhrzeigersinn begonnen werden soll. Wenn „true“, bedeutet dies gegen den Uhrzeigersinn, und wenn „false“, bedeutet es im Uhrzeigersinn. Der Parameter gegen den Uhrzeigersinn ist optional und hat standardmäßig den Wert „false“, was „im Uhrzeigersinn“ bedeutet. 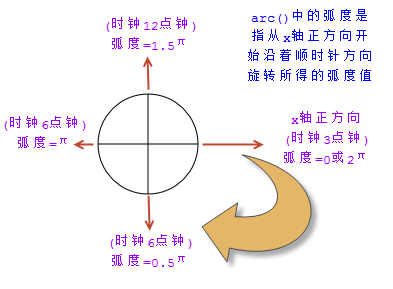
Radiant-Berechnungsmethode in der arc()-Methode
- arcTo(x1, y1, x2, y2, radius)
Diese Methode verwendet den Winkel, der durch den aktuellen Endpunkt, Endpunkt 1 (x1, y1) und Endpunkt 2 (x2, y2) gebildet wird, und zeichnet dann einen Abschnitt, der beide Seiten des Winkels tangiert und einen Radius von hat Radius Ein Bogen auf einem Kreis. Im Allgemeinen ist die Startposition beim Zeichnen eines Bogens der aktuelle Endpunkt, die Endposition ist Endpunkt 2 und die Richtung beim Zeichnen des Bogens ist die Richtung des kürzesten Bogens, der die beiden Endpunkte verbindet. Wenn sich der aktuelle Endpunkt nicht auf dem angegebenen Kreis befindet, zeichnet diese Methode außerdem eine gerade Linie vom aktuellen Endpunkt zum Startpunkt des Bogens.
Da es viel Platz gibt, um die arcTo()-Methode im Detail vorzustellen, sehen Sie sich bitte hier die detaillierte Verwendung von arcTo() an.
Nachdem wir die obige API zum Zeichnen von Bögen auf der Leinwand verstanden haben, werfen wir einen Blick darauf, wie man arc() zum Zeichnen von Bögen verwendet. Wir wissen bereits, dass der 4. und 5. Parameter, den arc() empfängt, den Anfangs- und Endbogenmaß des Bogens darstellen. Ich glaube, dass alle Leser in Mathematik- oder Geometriekursen in der Schule etwas über das Bogenmaß gelernt haben. Das Bogenmaß ist eine Winkeleinheit. Für einen Bogen, dessen Bogenlänge gleich seinem Radius ist, beträgt der Mittelpunktswinkel, den er einschließt, 1 Bogenmaß. Wir wissen auch, dass ein Kreis mit Radius r einen Umfang von 2πr hat. Mit diesen Geometriekenntnissen können wir die arc()-Methode zum Zeichnen von Bögen verwenden.
Verwenden Sie die Leinwand, um Bögen zu zeichnen
Jetzt zeichnen wir einen Viertelbogen eines Kreises mit einem Radius von 50 Pixeln.
- "UTF-8"
- >
HTML5 Canvas Drawing Arc Erste Schritte - width="400px"
- height="300px"
- style="border: 1px solid red;"> Ihr Browser unterstützt das Canvas-Tag nicht.
-
Der entsprechende Anzeigeeffekt ist wie folgt:
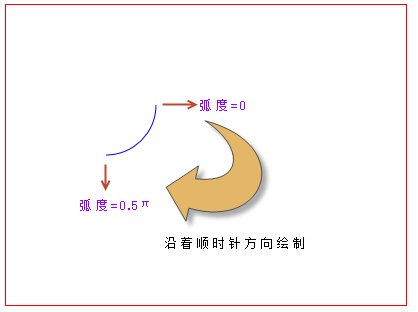
Zeichnen Sie mit der Leinwand einen Bogen im Uhrzeigersinn
Wie oben gezeigt, legen wir die Mittelpunktskoordinaten des Kreises, in dem sich der gezeichnete Bogen befindet, auf (100,100) und den Radius auf 50 Pixel fest. Da der Umfang eines Kreises mit dem Radius r 2πr beträgt, d. solange das Bogenmaß π/2 (also 90°) beträgt. Im obigen Code verwenden wir die Konstante Math.PI, die π in JavaScript darstellt.Außerdem legen wir im obigen Code auch die Richtung zum Zeichnen von Bögen auf den Uhrzeigersinn fest (falsch). Da der Anfangsbogenmaß 0 und der Endbogenmaß π/2 ist, wird der Bogen im Uhrzeigersinn ausgehend von der positiven Richtung der x-Achse gezeichnet, was zu der obigen Grafik führt. Welchen Effekt hat es, wenn wir im obigen Code die Zeichenrichtung des Bogens in Gegenuhrzeigersinn ändern?
JavaScript-CodeInhalt in die Zwischenablage kopieren- Der entsprechende Anzeigeeffekt ist wie folgt:
- JavaScript-Code
-
- Remarque : le paramètre de début de radian startRad et le paramètre de fin de radian endRad dans la méthode arc() sont tous deux en radians. Même si vous remplissez un nombre, tel que 360, il sera toujours considéré comme 360 radians. Quelles sont les conséquences de la définition de l'arc final du code ci-dessus sur 360 ? Cela dépend de la direction du dessin (c'est-à-dire de la valeur du paramètre anti-horaire). S'il est dessiné dans le sens des aiguilles d'une montre (faux), un cercle complet sera dessiné ; s'il est dessiné dans le sens inverse des aiguilles d'une montre, les radians supérieurs à 2π seront convertis en un ; radians égaux mais non supérieurs à 2π. Par exemple, définissez l'arc de fin dans le code ci-dessus sur 3π (Math.PI * 3). Si le sens inverse des aiguilles d'une montre est faux, il sera affiché sous la forme d'un cercle complet. Si c'est vrai, l'effet d'affichage sera le même que lorsqu'il est affiché. est réglé sur π. L’effet est cohérent.
- Lorsque l'arc de fin est réglé sur 3π, l'effet de dessin de la (fausse) rotation dans le sens des aiguilles d'une montre
Der entsprechende Anzeigeeffekt ist wie folgt:
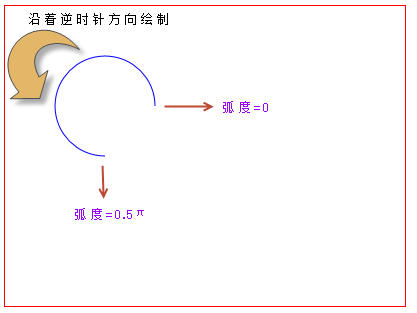
Zeichnen Sie mit der Leinwand einen Bogen gegen den Uhrzeigersinn
Verwenden Sie die Leinwand, um einen Kreis zu zeichnenNachdem wir gelernt haben, Bögen zu zeichnen, ist es einfach, Kreise analog zu zeichnen. Wir müssen nur den Endbogen des obigen Codes in 2π ändern.
JavaScript-CodeInhalt in die Zwischenablage kopierenLorsque l'arc de fin est réglé sur 3π, l'effet de dessin de la rotation (vraie) dans le sens inverse des aiguilles d'une montre
In Verbindung stehende Artikel
Mehr sehen- Das Vollbild-Bildlauf-Plug-in AlloyTouch erstellt in 30 Sekunden eine flüssige H5-Seite
- Tatsächlicher HTML5-Kampf und Analyse von Touch-Ereignissen (Touchstart, Touchmove und Touchend)
- Ausführliche Erläuterung der Beispiele für Bildzeichnungen in HTML5 Canvas 9
- Reguläre Ausdrücke und neue HTML5-Elemente
- So kombinieren Sie NodeJS und HTML5, um mehrere Dateien per Drag-and-Drop auf den Server hochzuladen

