Heim >Backend-Entwicklung >Python-Tutorial >Analyse des PyNeuraLogic-Quellcodes der Python-Architektur
Analyse des PyNeuraLogic-Quellcodes der Python-Architektur
- WBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBOYWBnach vorne
- 2023-06-03 14:05:271096Durchsuche
Einführung
Die Leistungsfähigkeit der neurosymbolischen Programmierung zeigen
1 Einführung
In den letzten Jahren haben wir den Aufstieg transformatorbasierter Modelle erlebt und in vielen Bereichen wie der Verarbeitung natürlicher Sprache oder Computer Vision Ergebnisse erzielt . erfolgreiche Bewerbung. In diesem Artikel werden wir eine prägnante, interpretierbare und skalierbare Möglichkeit untersuchen, Deep-Learning-Modelle, insbesondere Transformer, als Hybridarchitektur auszudrücken, d. h. durch die Kombination von Deep Learning mit symbolischer künstlicher Intelligenz. Daher werden wir das Modell in einem neurosymbolischen Python-Framework namens PyNeuraLogic implementieren.
Durch die Kombination symbolischer Darstellung mit Deep Learning schließen wir Lücken in aktuellen Deep-Learning-Modellen, wie z. B. Out-of-the-Box-Interpretierbarkeit und fehlende Inferenztechniken. Möglicherweise ist die Erhöhung der Anzahl der Parameter nicht der sinnvollste Weg, um diese gewünschten Ergebnisse zu erzielen, ebenso wie eine Erhöhung der Megapixelzahl einer Kamera nicht unbedingt zu besseren Fotos führt.
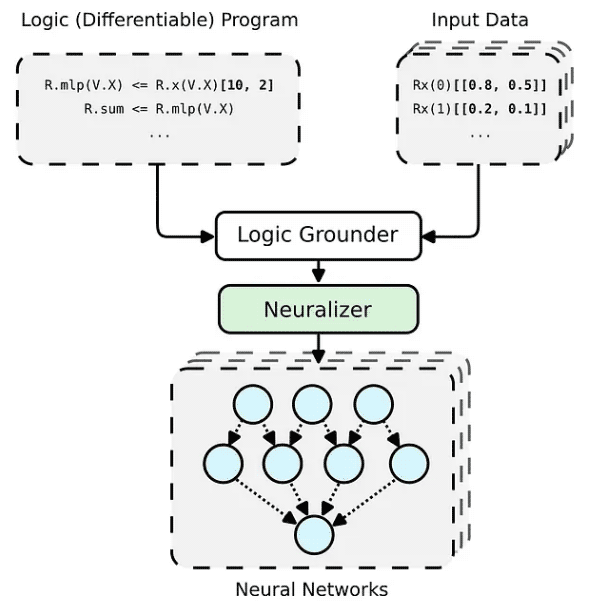
Das PyNeuraLogic-Framework basiert auf Logikprogrammierung – Logikprogramme enthalten differenzierbare Parameter. Das Framework eignet sich gut für kleinere strukturierte Daten (z. B. Moleküle) und komplexe Modelle (z. B. Transformatoren und graphische neuronale Netze). PyNeuraLogic ist nicht die beste Wahl für nicht relationale und große Tensordaten.
Die Schlüsselkomponente des Frameworks ist ein differenzierbares Logikprogramm, das wir Vorlage nennen. Eine Vorlage besteht aus logischen Regeln, die die Struktur eines neuronalen Netzwerks auf abstrakte Weise definieren – wir können uns eine Vorlage als Blaupause für die Architektur des Modells vorstellen. Die Vorlage wird dann auf jede Eingabedateninstanz angewendet, um (durch Basis und Neuralisierung) ein neuronales Netzwerk zu generieren, das für die Eingabeprobe eindeutig ist. Dieser Prozess unterscheidet sich völlig von anderen vordefinierten Architekturen und kann sich nicht an unterschiedliche Eingabebeispiele anpassen.
2. Symbolische Transformatoren
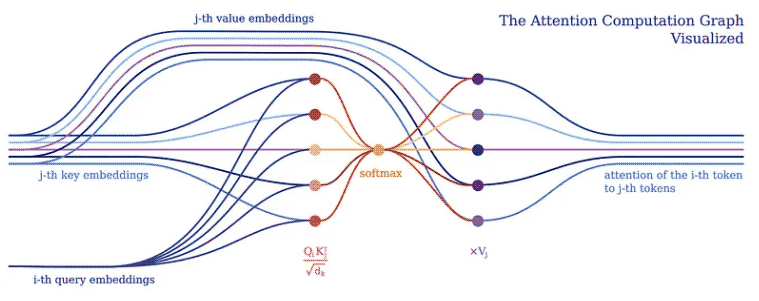
Normalerweise implementieren wir das Deep-Learning-Modell, um Tensoroperationen an Stapeln von Eingabe-Tokens in einem großen Tensor durchzuführen. Dies ist sinnvoll, da Deep-Learning-Frameworks und Hardware (z. B. GPUs) im Allgemeinen für die Verarbeitung größerer Tensoren optimiert sind und nicht für die Verarbeitung mehrerer Tensoren unterschiedlicher Form und Größe. Transformatoren bilden hier keine Ausnahme. Sie bündeln typischerweise eine einzelne Token-Vektordarstellung in einer großen Matrix und stellen das Modell als Operationen auf einer solchen Matrix dar. Allerdings verbirgt eine solche Implementierung die Beziehung zwischen einzelnen Eingabe-Tokens, wie der Aufmerksamkeitsmechanismus des Transformers zeigt.
3. Aufmerksamkeitsmechanismus
Der Aufmerksamkeitsmechanismus bildet den Kern aller Transformer-Modelle. Insbesondere verwendet die klassische Version die sogenannte Multi-Head-Scaling-Punktproduktaufmerksamkeit. Lassen Sie uns (aus Gründen der Übersichtlichkeit) einen Header verwenden, um die Aufmerksamkeit des skalierten Skalarprodukts in ein einfaches Logikprogramm zu zerlegen.
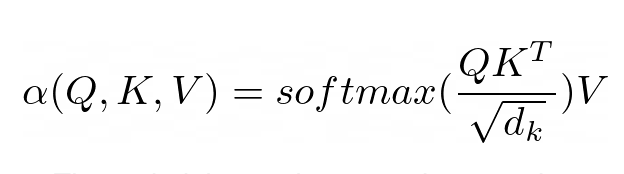
Der Zweck der Aufmerksamkeit besteht darin, zu entscheiden, auf welche Teile des Inputs sich das Netzwerk konzentrieren soll. Bei der Implementierung sollte auf den gewichteten berechneten Wert V geachtet werden. Das Gewicht stellt die Kompatibilität des Eingabeschlüssels K und der Abfrage Q dar. In dieser speziellen Version werden die Gewichte durch die Softmax-Funktion des Skalarprodukts von Abfrage Q und Abfrageschlüssel K, dividiert durch die Quadratwurzel der Dimension d_k des Eingabemerkmalsvektors, berechnet.
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product]
In PyNeuraLogic können wir den Aufmerksamkeitsmechanismus durch die oben genannten logischen Regeln vollständig erfassen. Die erste Regel stellt die Berechnung des Gewichts dar – sie berechnet das Produkt aus der inversen Quadratwurzel der Dimension und dem transponierten j-ten Schlüsselvektor und i-ten Abfragevektor. Als nächstes verwenden wir die Softmax-Funktion, um die Ergebnisse von i mit allen möglichen j zu aggregieren.
Die zweite Regel berechnet dann das Produkt zwischen diesem Gewichtsvektor und dem entsprechenden j-ten Wertvektor und summiert die Ergebnisse für verschiedene j für jeden i-ten Token.
4. Aufmerksamkeitsmaskierung
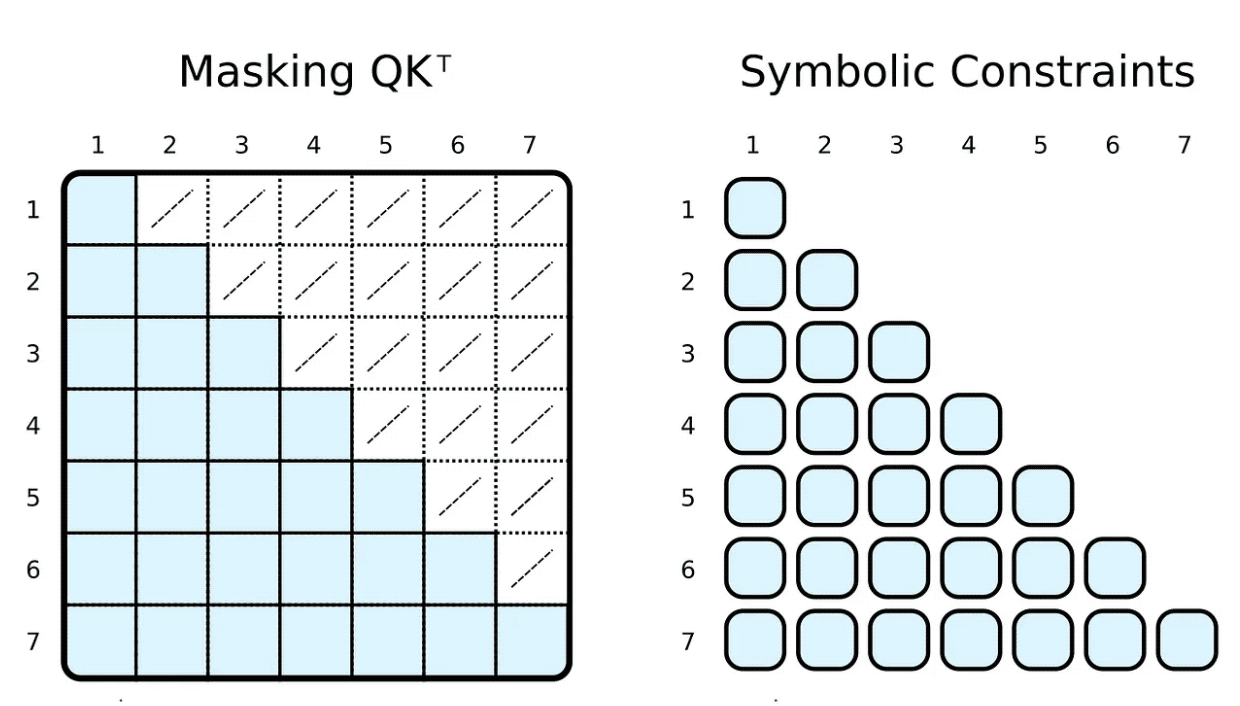
Während des Trainings und der Bewertung schränken wir oft ein, woran das Eingabetoken teilnehmen kann. Beispielsweise möchten wir Markierungen einschränken, um nach vorne zu blicken und uns auf kommende Wörter zu konzentrieren. Gängige Frameworks wie PyTorch erreichen dies durch Maskierung, d. h. indem sie eine Teilmenge von Elementen des skalierten Skalarproduktergebnisses auf eine sehr niedrige negative Zahl setzen. Diese Zahlen geben an, dass die Softmax-Funktion gezwungen ist, die Gewichtung des entsprechenden Tag-Paares auf Null zu setzen.
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I), R.special.leq(V.J, V.I)
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],Wir können dies leicht erreichen, indem wir unseren Symbolen Körperbeziehungsbeschränkungen hinzufügen. Um das Gewicht zu berechnen, beschränken wir den i-ten Indikator darauf, größer oder gleich dem j-ten Indikator zu sein. Im Gegensatz zu Masken berechnen wir nur das erforderliche skalierte Skalarprodukt.
5. Nicht standardmäßige Aufmerksamkeit
Natürlich kann die symbolische „Maskierung“ völlig willkürlich sein. Die meisten Menschen haben vom spärlichen transformatorbasierten GPT-3⁴ oder seinen Anwendungen wie ChatGPT gehört. ⁵ Aufmerksamkeit (Schrittversion) des Sparse-Transformators hat zwei Arten von Aufmerksamkeitsköpfen:
一个只关注前 n 个标记 (0 ≤ i − j ≤ n)
一个只关注每第 n 个前一个标记 ((i − j) % n = 0)
两种类型的头的实现都只需要微小的改变(例如,对于 n = 5)。
(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.leq(V.D, 5), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],(R.weights(V.I, V.J) <= (
R.d_k, R.k(V.J).T, R.q(V.I),
R.special.mod(V.D, 5, 0), R.special.sub(V.I, V.J, V.D),
)) | [F.product, F.softmax_agg(agg_terms=[V.J])],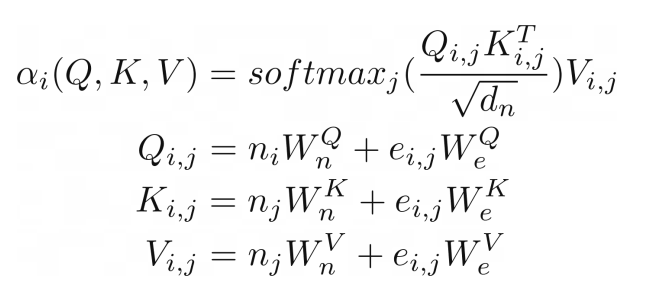
我们可以进一步推进,将类似图形输入的注意力概括到关系注意力的程度。⁶ 这种类型的注意力在图形上运行,其中节点只关注它们的邻居(由边连接的节点)。结果是节点向量嵌入和边嵌入的键 K、查询 Q 和值 V 相加。
(R.weights(V.I, V.J) <= (R.d_k, R.k(V.I, V.J).T, R.q(V.I, V.J))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.I, V.J)) | [F.product], R.q(V.I, V.J) <= (R.n(V.I)[W_qn], R.e(V.I, V.J)[W_qe]), R.k(V.I, V.J) <= (R.n(V.J)[W_kn], R.e(V.I, V.J)[W_ke]), R.v(V.I, V.J) <= (R.n(V.J)[W_vn], R.e(V.I, V.J)[W_ve]),
在我们的示例中,这种类型的注意力与之前展示的点积缩放注意力几乎相同。唯一的区别是添加了额外的术语来捕获边缘。将图作为注意力机制的输入似乎很自然,这并不奇怪,因为 Transformer 是一种图神经网络,作用于完全连接的图(未应用掩码时)。在传统的张量表示中,这并不是那么明显。
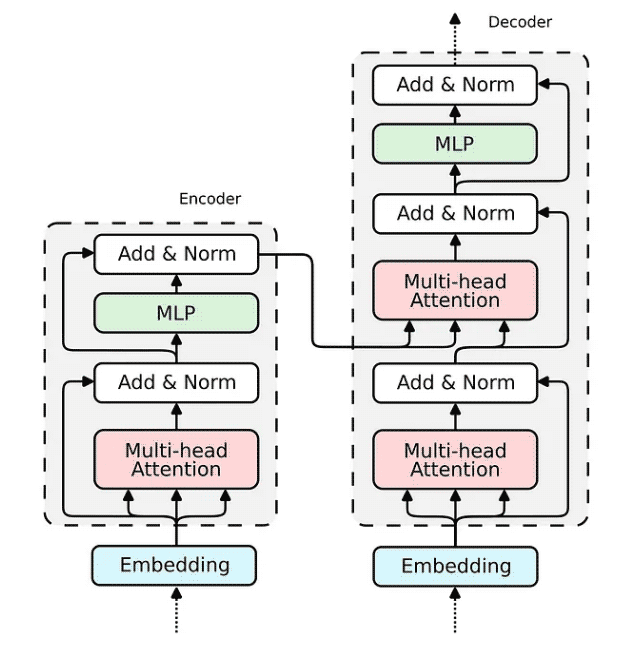
6. Encoder
现在,当我们展示 Attention 机制的实现时,构建整个 transformer 编码器块的缺失部分相对简单。
如何在 Relational Attention 中实现嵌入已经为我们所展现。对于传统的 Transformer,嵌入将非常相似。我们将输入向量投影到三个嵌入向量中——键、查询和值。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v],
查询嵌入通过跳过连接与注意力的输出相加。然后将生成的向量归一化并传递到多层感知器 (MLP)。
(R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm],
对于 MLP,我们将实现一个具有两个隐藏层的全连接神经网络,它可以优雅地表达为一个逻辑规则。
(R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu],
最后一个带有规范化的跳过连接与前一个相同。
(R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
所有构建 Transformer 编码器所需的组件都已经被构建完成。解码器使用相同的组件;因此,其实施将是类似的。让我们将所有块组合成一个可微分逻辑程序,该程序可以嵌入到 Python 脚本中并使用 PyNeuraLogic 编译到神经网络中。
R.q(V.I) <= R.input(V.I)[W_q], R.k(V.I) <= R.input(V.I)[W_k], R.v(V.I) <= R.input(V.I)[W_v], R.d_k[1 / math.sqrt(embed_dim)], (R.weights(V.I, V.J) <= (R.d_k, R.k(V.J).T, R.q(V.I))) | [F.product, F.softmax_agg(agg_terms=[V.J])], (R.attention(V.I) <= (R.weights(V.I, V.J), R.v(V.J)) | [F.product], (R.norm1(V.I) <= (R.attention(V.I), R.q(V.I))) | [F.norm], (R.mlp(V.I)[W_2] <= (R.norm(V.I)[W_1])) | [F.relu], (R.norm2(V.I) <= (R.mlp(V.I), R.norm1(V.I))) | [F.norm],
Das obige ist der detaillierte Inhalt vonAnalyse des PyNeuraLogic-Quellcodes der Python-Architektur. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

