Heim >Java >javaLernprogramm >So verwenden Sie die sieben Sortiermethoden von Java-Datenstrukturen
So verwenden Sie die sieben Sortiermethoden von Java-Datenstrukturen
- 王林nach vorne
- 2023-06-02 19:19:231576Durchsuche
1. Direkte Einfügungssortierung
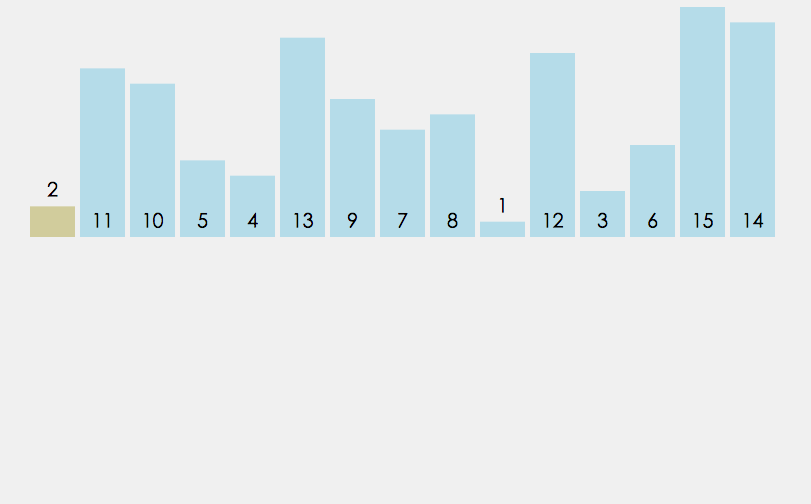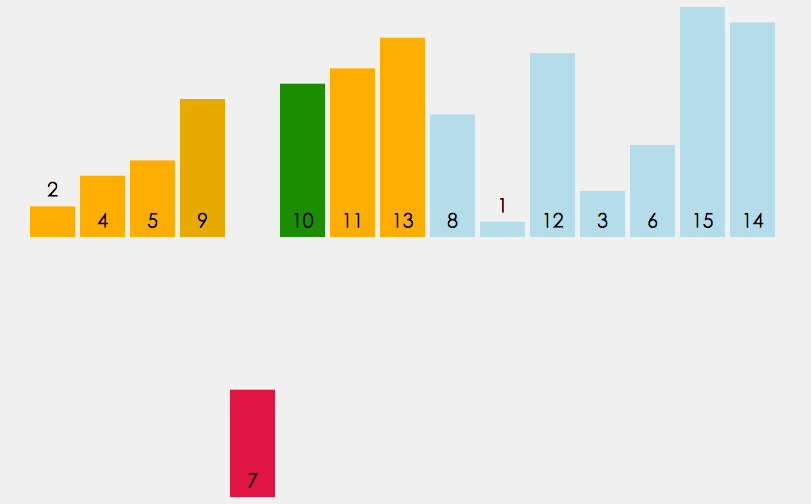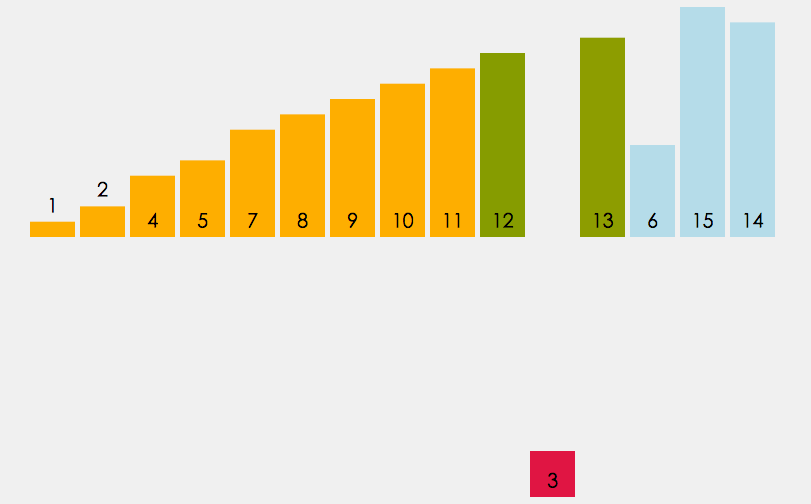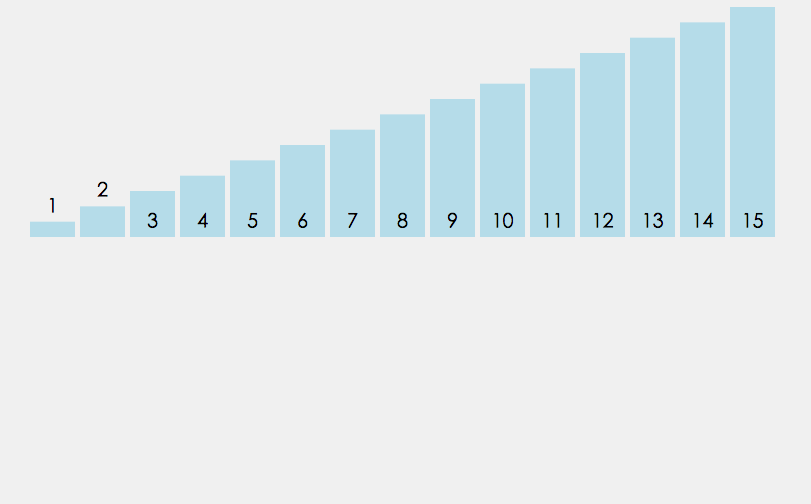
Beim Einfügen des i (i>=1)-Elements wird das vorherige Array[0],array[1],…,array[i -1 ] wurde sortiert. Vergleichen Sie zu diesem Zeitpunkt array[i] mit array[i-1], array[i-2],..., um die Einfügeposition zu finden und array[i] an der ursprünglichen Position einzufügen Gehen Sie der Reihe nach rückwärts.
Je näher die Daten an der Reihenfolge liegen, desto weniger Zeit dauert es, die Sortierung direkt einzufügen.
Zeitkomplexität: O(N^2)
Raumkomplexität O(1), es ist ein stabiler Algorithmus
Direkte Einfügungssortierung:
public static void insertSort(int[] array){
for (int i = 1; i < array.length; i++) {
int tmp=array[i];
int j=i-1;
for(;j>=0;--j){
if(array[j]>tmp){
array[j+1]=array[j];
}else{
break;
}
}
array[j+1]=tmp;
}
} 2. Hill-Sortierung
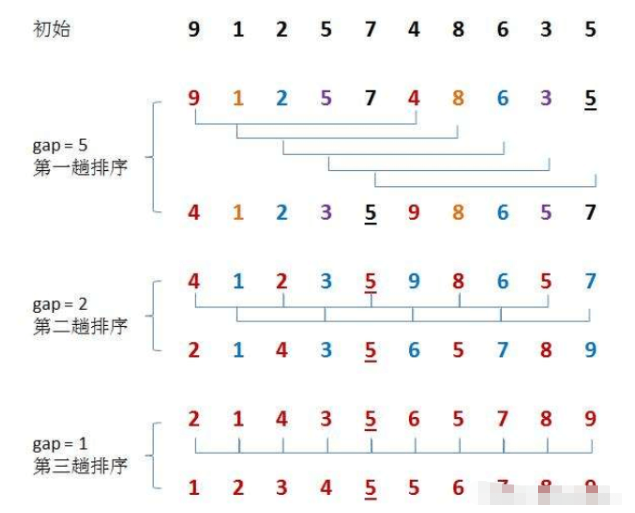
2. Hill-Sortierung
Hill-Sortierung Die Grundidee von Die Methode lautet: Wählen Sie zunächst eine ganzzahlige Lücke aus, teilen Sie alle zu sortierenden Datensätze in der Datei in Lückengruppen auf, fügen Sie alle Zahlen mit einem Lückenabstand in dieselbe Gruppe ein und führen Sie eine direkte Einfügungssortierung für die Zahlen in jeder Gruppe durch . Nehmen Sie dann „gap=gap/2“ und wiederholen Sie die obige Gruppierungs- und Sortierarbeit. Bei Gap=1 werden alle Zahlen direkt innerhalb einer Gruppe sortiert.
- Hill Sort ist eine Optimierung der Direkteinfügungssortierung.
- Der Zweck besteht darin, das Array näher an die Ordnung zu bringen, sodass eine Vorsortierung durchgeführt wird, wenn die Lücke > 1 ist. Durch Einfügungssortierung kann ein nahezu geordnetes Array schnell sortiert werden, wenn die Lücke 1 beträgt.
- Die zeitliche Komplexität der Hill-Sortierung ist schwer zu berechnen, da es viele Möglichkeiten gibt, die Lücke zu berechnen, was die Berechnung erschwert.
- Hill-Sortierung:
public static void shellSort(int[] array){
int size=array.length;
//这里定义gap的初始值为数组长度的一半
int gap=size/2;
while(gap>0){
//间隔为gap的直接插入排序
for (int i = gap; i < size; i++) {
int tmp=array[i];
int j=i-gap;
for(;j>=0;j-=gap){
if(array[j]>tmp){
array[j+gap]=array[j];
}else{
break;
}
}
array[j+gap]=tmp;
}
gap/=2;
}
} 2. Auswahlsortierung
Wählen Sie das kleinste Datenelement im Elementsatz array[i]--array[n-1]
2. Auswahlsortierung
Wählen Sie das kleinste Datenelement im Elementsatz array[i]--array[n-1]aus
- Wenn es nicht das erste Element in diesem Set ist, tauschen Sie es mit dem ersten Element in diesem Set aus.
- Im verbleibenden Set wiederholen Sie die obigen Schritte, bis noch 1 Element im Set übrig ist.
- Zeitliche Komplexität : O(N^2)Raumkomplexität ist O(1), instabil
//交换
private static void swap(int[] array,int i,int j){
int tmp=array[i];
array[i]=array[j];
array[j]=tmp;
}
//选择排序
public static void chooseSort(int[] array){
for (int i = 0; i < array.length; i++) {
int minIndex=i;//记录最小值的下标
for (int j = i+1; j < array.length; j++) {
if (array[j]<array[minIndex]) {
minIndex=j;
}
}
swap(array,i,minIndex);
}
}2. Heap-Sortierung
Zwei Ideen der Heap-Sortierung (am Beispiel der aufsteigenden Reihenfolge): 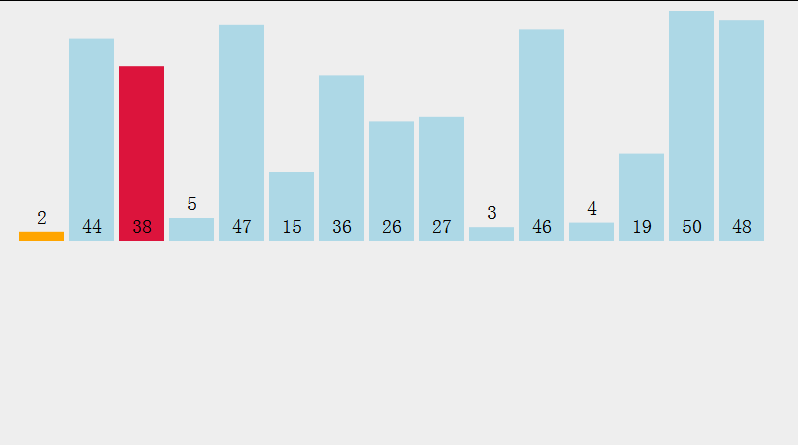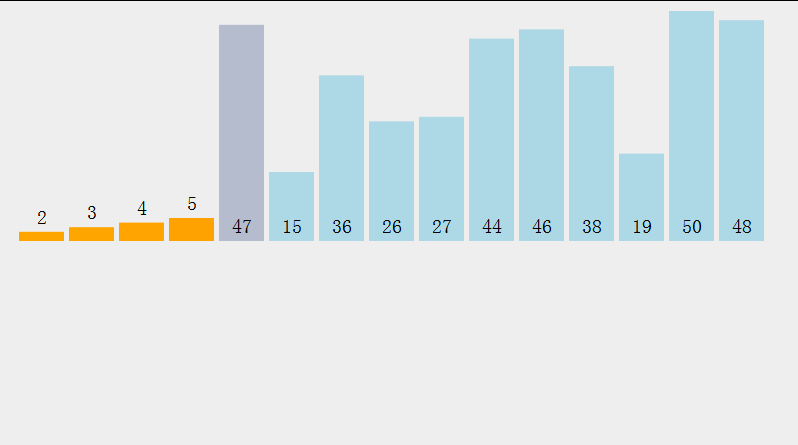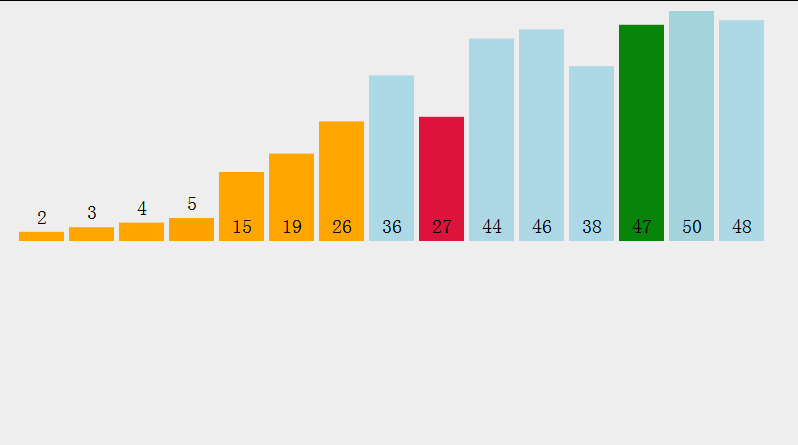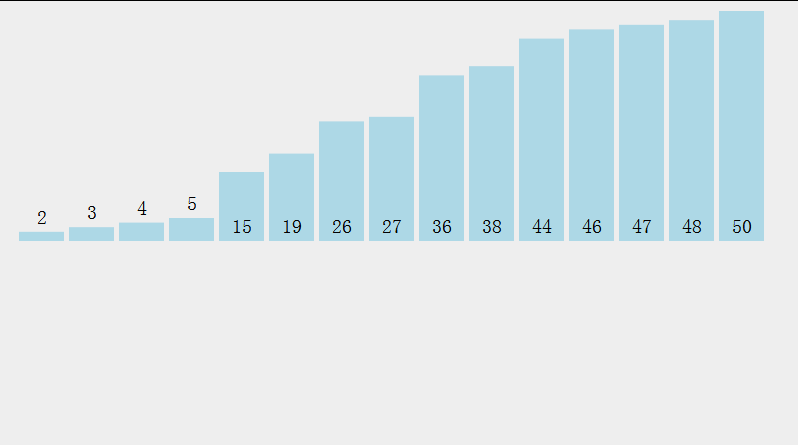
- Erstellen Sie einen großen Root-Heap und definieren Sie den Endelement-Positionsschlüssel des Heaps , und tauschen Sie jedes Mal den oberen Rand des Heaps aus. Das Element und das Element an der Schlüsselposition (key--), bis der Schlüssel den oberen Rand des Heaps erreicht. Zu diesem Zeitpunkt erfolgt die hierarchische Durchquerung der Elemente im Heap aufsteigend Reihenfolge (wie folgt)
- Zeitkomplexität: O(N^2)Raumkomplexität: O(N), instabil
//向下调整
public static void shiftDown(int[] array,int parent,int len){
int child=parent*2+1;
while(child<len){
if(child+1<len){
if(array[child+1]>array[child]){
child++;
}
}
if(array[child]>array[parent]){
swap(array,child,parent);
parent=child;
child=parent*2+1;
}else{
break;
}
}
}
//创建大根堆
private static void createHeap(int[] array){
for (int parent = (array.length-1-1)/2; parent >=0; parent--) {
shiftDown(array,parent,array.length);
}
}
//堆排序
public static void heapSort(int[] array){
//创建大根堆
createHeap(array);
//排序
for (int i = array.length-1; i >0; i--) {
swap(array,0,i);
shiftDown(array,0,i);
}
}3. Austauschsortierung
1 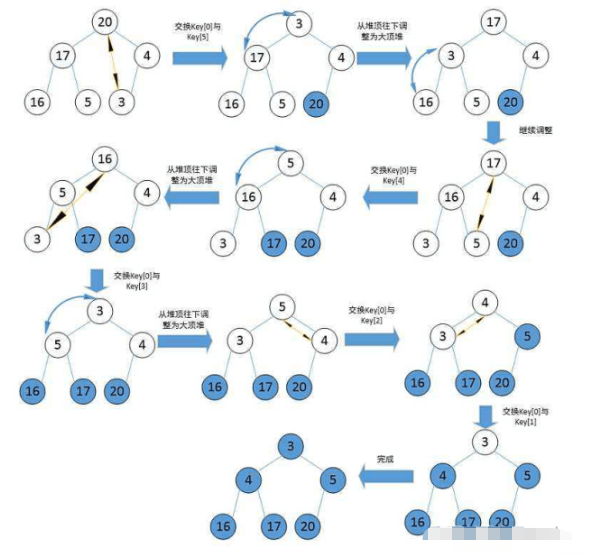
public static void bubbleSort(int[] array){
for(int i=0;i<array.length-1;++i){
int count=0;
for (int j = 0; j < array.length-1-i; j++) {
if(array[j]>array[j+1]){
swap(array,j,j+1);
count++;
}
}
if(count==0){
break;
}
}
}2. Jede zu sortierende Auswahl ist sicher Gemäß diesem Sortiercode wird die zu sortierende Menge in zwei Teilsequenzen unterteilt. Alle Elemente in der linken Teilsequenz sind kleiner als der Benchmark-Wert größer als der Benchmark-Wert. Dann wird die ganz linke Teilsequenz wiederholt. Die Sequenz wiederholt diesen Vorgang, bis alle Elemente an ihren entsprechenden Positionen angeordnet sind.
Zeitkomplexität: Bestes O(n*logn): Die zu sortierende Sequenz kann jedes Mal so gleichmäßig wie möglich aufgeteilt werden
public static void quickSort(int[] array,int left,int right){
if(left>=right){
return;
}
int l=left;
int r=right;
int tmp=array[l];
while(l<r){
while(array[r]>=tmp&&l<r){
//等号不能省略,如果省略,当序列中存在相同的值时,程序会死循环
r--;
}
array[l]=array[r];
while(array[l]<=tmp&&l<r){
l++;
}
array[r]=array[l];
}
array[l]=tmp;
quickSort(array,0,l-1);
quickSort(array,l+1,right);
}(2) Optimierung der SchnellsortierungWählen Sie den Schlüssel, indem Sie die Mitte von drei Zahlen nehmen Was die Auswahl der Schlüsselwerte betrifft: Wenn die zu sortierende Reihenfolge in Ordnung ist, wählen wir den ersten oder letzten aus Der Schlüssel, der zur Segmentierung führen kann. Die linke oder rechte Seite ist leer. In diesem Fall ist die Platzkomplexität der schnellen Sortierung relativ groß, was leicht zu einem Stapelüberlauf führen kann. Dann können wir die Drei-Zahlen-Methode verwenden, um diese Situation zu beseitigen. Als Schlüsselwert wird der mittlere Wert des ersten, letzten und mittleren Elements in der Sequenz verwendet. //key值的优化,只在快速排序中使用,则可以为private
private int threeMid(int[] array,int left,int right){
int mid=(left+right)/2;
if(array[left]>array[right]){
if(array[mid]>array[left]){
return left;
}
return array[mid]<array[right]?right:mid;
}else{
if(array[mid]<array[left]){
return left;
}
return array[mid]>array[right]?right:mid;
}
}Bei der Rekursion in einen kleinen Teilbereich können Sie die Verwendung der Einfügungssortierung in Betracht ziehen
随着我们递归的进行,区间会变的越来越小,我们可以在区间小到一个值的时候,对其进行插入排序,这样代码的效率会提高很多。
(3)快速排序的非递归实现
//找到一次划分的下标
public static int patition(int[] array,int left,int right){
int tmp=array[left];
while(left<right){
while(left<right&&array[right]>=tmp){
right--;
}
array[left]=array[right];
while(left<right&&array[left]<=tmp){
left++;
}
array[right]=array[left];
}
array[left]=tmp;
return left;
}
//快速排序的非递归
public static void quickSort2(int[] array){
Stack<Integer> stack=new Stack<>();
int left=0;
int right=array.length-1;
stack.push(left);
stack.push(right);
while(!stack.isEmpty()){
int r=stack.pop();
int l=stack.pop();
int p=patition(array,l,r);
if(p-1>l){
stack.push(l);
stack.push(p-1);
}
if(p+1<r){
stack.push(p+1);
stack.push(r);
}
}
}四、归并排序
归并排序(MERGE-SORT):该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。实现序列的完全有序,需要将已经有序的子序列合并,即先让每个子序列有序,然后再将相邻的子序列段有序。若将两个有序表合并成一个有序表,称为二路归并。
时间复杂度:O(n*logN)(无论有序还是无序)
空间复杂度:O(N)。是稳定的排序。
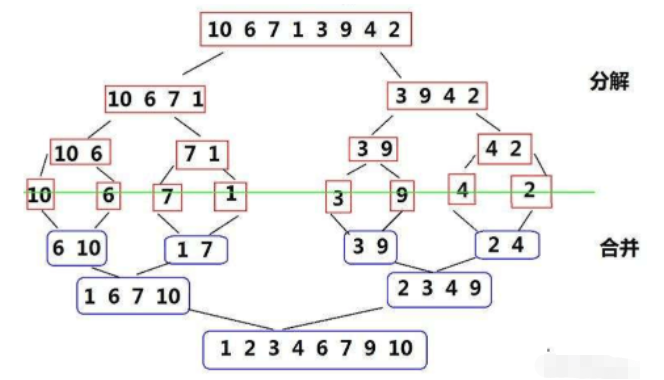
//归并排序:递归
public static void mergeSort(int[] array,int left,int right){
if(left>=right){
return;
}
int mid=(left+right)/2;
//递归分割
mergeSort(array,left,mid);
mergeSort(array,mid+1,right);
//合并
merge(array,left,right,mid);
}
//非递归
public static void mergeSort1(int[] array){
int gap=1;
while(gap<array.length){
for (int i = 0; i < array.length; i+=2*gap) {
int left=i;
int mid=left+gap-1;
if(mid>=array.length){
mid=array.length-1;
}
int right=left+2*gap-1;
if(right>=array.length){
right=array.length-1;
}
merge(array,left,right,mid);
}
gap=gap*2;
}
}
//合并:合并两个有序数组
public static void merge(int[] array,int left,int right,int mid){
int[] tmp=new int[right-left+1];
int k=0;
int s1=left;
int e1=mid;
int s2=mid+1;
int e2=right;
while(s1<=e1&&s2<=e2){
if(array[s1]<=array[s2]){
tmp[k++]=array[s1++];
}else{
tmp[k++]=array[s2++];
}
}
while(s1<=e1){
tmp[k++]=array[s1++];
}
while(s2<=e2){
tmp[k++]=array[s2++];
}
for (int i = left; i <= right; i++) {
array[i]=tmp[i-left];
}
}五、排序算法的分析
| 排序方法 | 最好时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
| 直接插入排序 | O(n) | O(n^2) | O(1) | 稳定 |
| 希尔排序 | O(n) | O(n^2) | O(1) | 不稳定 |
| 直接排序 | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(nlog(2)n) | O(nlog(2)n) | O(1) | 不稳定 |
| 冒泡排序 | O(n) | O(n^2) | O(1) | 稳定 |
| 快速排序 | O(nlog(2)n) | O(n^2) | O(nlog(2)n) | 不稳定 |
| 归并排序 | O(nlog(2)n) | O(nlog(2)n) | O(n) | 稳定 |
Das obige ist der detaillierte Inhalt vonSo verwenden Sie die sieben Sortiermethoden von Java-Datenstrukturen. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!

