So implementieren Sie den Python-Suchalgorithmus

Suchalgorithmus wird verwendet, um abzurufen, ob bestimmte Daten (Schlüsselwort) in Sequenzdaten (Population) vorhanden sind:

• Lineare Suche: Die lineare Suche wird auch als sequentielle Suche bezeichnet und in ungeordneten Sequenzen verwendet .

• Binäre Suche: Die binäre Suche wird auch Halbsuche genannt und ihr Algorithmus wird für geordnete Sequenzen verwendet.

• Interpolationssuche: Die Interpolationssuche ist eine Verbesserung gegenüber dem binären Suchalgorithmus.

• Blockierte Suche: Auch als indexsequentielle Suche bekannt, handelt es sich um eine verbesserte Version der linearen Suche.

• Baumtabellensuche: Die Baumtabellensuche kann in einen binären Suchbaum und eine ausgewogene binäre Baumsuche unterteilt werden.

• Hash-Suche: Mit der Hash-Suche können die erforderlichen Daten direkt anhand von Schlüsselwörtern gefunden werden.

Da die Baumtabellensuche und die Hashsuche viel Platz benötigen, werden sie in diesem Artikel nicht erläutert. Dieser Artikel bietet einen umfassenden Überblick über Suchalgorithmen über baumbasierte und hashbasierte Ansätze hinaus. Er analysiert die Stärken und Schwächen jedes Algorithmus und schlägt entsprechende Optimierungsstrategien vor.

1. Lineare Suche

Sequentielle Suche, auch als lineare Suche bekannt, ist ein Algorithmus, der auf primitiver, erschöpfender und Brute-Force-Suche basiert. Es ist leicht zu verstehen und die Codierungsimplementierung ist einfach. Wenn die verarbeitete Datenmenge groß ist, kann die Leistung aufgrund der relativ einfachen Idee des Algorithmus und des Fehlens eines optimalen Algorithmusdesigns geringer sein.

Idee der linearen Suche:

• Scannen Sie alle Daten in der Originalliste einzeln von Anfang bis Ende und vergleichen Sie sie mit dem angegebenen Schlüsselwort.

• Wenn der Vergleich gleich ist, ist die Suche erfolgreich.

• Wenn der Scan abgeschlossen ist und immer noch keine Daten gefunden werden, die dem angegebenen Schlüsselwort entsprechen, wird die Suche als fehlgeschlagen erklärt.

Gemäß der Beschreibung des linearen Suchalgorithmus ist es einfach zu programmieren und zu implementieren:

'''
线性查找算法
参数：
    nums: 序列
    key:关键字
返回值：
    关键字在序列中的位置
    如果没有，则返回 -1
'''
def line_find(nums, key):
    for i in range(len(nums)):
        if nums[i] == key:
            return i
    return -1
'''
测试线性算法
'''
if __name__ == "__main__":
    nums = [4, 1, 8, 10, 3, 5]
    key = int(input("请输入要查找的关键字："))
    pos = line_find(nums, key)
    print("关键字 {0} 在数列的第 {1} 位置".format(key, pos))
'''
输出结果：
请输入要查找的关键字：3
关键字 3 在数列的 4 位置
'''

Durchschnittliche Zeitkomplexitätsanalyse des linearen Suchalgorithmus.

1. Glücksfall: Wenn das gesuchte Schlüsselwort zufällig an erster Stelle der Sequenz steht, müssen Sie es nur einmal suchen.

Suchen Sie beispielsweise nach dem Schlüsselwort 4 in der Reihenfolge = [4,1,8,10,3,5].

Nur 1 Mal suchen.

2. Der schlimmste Glücksfall: Das Schlüsselwort wird erst gefunden, wenn das Ende der Sequenz gescannt wird.

Finden Sie beispielsweise heraus, ob das Schlüsselwort 5 in der Sequenz = [4,1,8,10,3,5] vorhanden ist.

Die Anzahl der erforderlichen Suchvorgänge entspricht der Länge der Sequenz, die hier das Sechsfache beträgt.

3. Glück oder Pech: Wenn das Schlüsselwort, das Sie finden möchten, irgendwo in der Mitte der Sequenz liegt, beträgt die Wahrscheinlichkeit, es zu finden, 1/n.

n ist die Länge der Sequenz.

Die durchschnittliche Anzahl der Suchvorgänge für die lineare Suche sollte = (1+n)/2 sein. Dieser Satz wird wie folgt umgeschrieben: Seine Zeitkomplexität ist O(n).

Konstanten werden in der großen O-Notation ignoriert.

Das Worst-Case-Szenario bei der linearen Suche ist: Nach dem Scannen des gesamten Arrays kann kein Schlüsselwort gefunden werden.

Suchen Sie beispielsweise nach dem Schlüsselwort 12 in der Reihenfolge = [4,1,8,10,3,5].

Nach sechsmaligem Scannen habe ich versagt! !

Verbesserter linearer Suchalgorithmus

kann den Linear Search-Algorithmus entsprechend optimieren. Zum Beispiel die Einrichtung eines „Außenpostens“. Der sogenannte „Außenposten“ besteht darin, vor der Suche das zu suchende 线性查找算法进行相应的优化。如设置“前哨站”。所谓“前哨站”，就是把要查找的关键字在查找之前插入到数列的尾部。

def line_find_(nums, key):
    i = 0
    while nums[i] != key:
        i += 1
    return -1 if i == len(nums)-1 else i

'''
测试线性算法
'''
if __name__ == "__main__":
    nums = [4, 1, 8, 10, 3, 5]
    key = int(input("请输入要查找的关键字："))
    # 查找之前，先把关键字存储到列到的尾部
    nums.append(key)
    pos = line_find_(nums, key)
    print("关键字 {0} 在数列的第 {1} 位置".format(key, pos))

用"前哨站"优化后的线性查找算法的时间复杂度没有变化，O(n)。或者说从 2 者代码上看，也没有太多变化。

但从代码的实际运行角度而言，第 2 种方案减少了 if 指令的次数，同样减少了编译后的指令，也就减少了 CPU执行指令的次数，这种优化属于微优化，不是算法本质上的优化。

使用计算机编程语言所编写的代码为伪指令代码。

经过编译后的指令代码叫 CPUSchlüsselwort

am Ende der Sequenz einzufügen.

'''
二分查找算法
'''
def binary_find(nums, key):
    # 初始左指针
    l_idx = 0
    # 初始在指针
    r_ldx = len(nums) - 1
    while l_idx <= r_ldx:
        # 计算出中间位置
        mid_pos = (r_ldx + l_idx) // 2
        # 计算中间位置的值
        mid_val = nums[mid_pos]
        # 与关键字比较
        if mid_val == key:
            # 出口一：比较相等，有此关键字，返回关键字所在位置
            return mid_pos
        elif mid_val > key:
            # 说明查找范围应该缩少在原数的左边
            r_ldx = mid_pos - 1
        else:
            l_idx = mid_pos + 1
    # 出口二：没有查找到给定关键字
    return -1

&#39;&#39;&#39;
测试二分查找
&#39;&#39;&#39;
if __name__ == "__main__":
    nums = [1, 3, 4, 5, 8, 10, 12]
    key = 3
    pos = binary_find(nums, key)
    print(pos)

Die zeitliche Komplexität des mit „Outpost“ optimierten linearen Suchalgorithmus hat sich nicht geändert, O(n). Mit anderen Worten: Aus der Perspektive von 2 oder dem Code gibt es nicht viele Änderungen.

Aber aus der Perspektive der tatsächlichen Ausführung des Codes reduziert die 2-Lösung die Anzahl der if-Anweisungen und auch die Anzahl der kompilierten Anweisungen, wodurch reduziert wird >CPUDie Häufigkeit, mit der eine Anweisung ausgeführt wird. Diese Art der Optimierung ist eine Mikrooptimierung, keine Optimierung der Natur des Algorithmus.

Mit einer Computerprogrammiersprache geschriebener Code ist Pseudo-Anweisungscode.

Der kompilierte Befehlscode wird als CPU-Befehlssatz bezeichnet.

• Eine Optimierungslösung besteht darin, den kompilierten Befehlssatz zu reduzieren.
  2. Binäre Suche
• Geordnete Suche bedeutet, dass die durchsuchten Daten in einer bestimmten Reihenfolge angeordnet werden müssen, und die binäre Suche ist eine geordnete Suche. Wenn Sie beispielsweise nach dem Schlüsselwort 4 in der Sequenz = [4,1,8,10,3,5,12] suchen, ist die Faktorsequenz nicht geordnet, sodass die binäre Suche nicht verwendet werden kann Bei einem binären Suchalgorithmus müssen Sie zunächst eine Zahlenfolge sortieren.
  Die binäre Suche nutzt die Idee des Halbierungsalgorithmus. Es gibt zwei Schlüsselinformationen im binären Suchalgorithmus, die jederzeit abgerufen werden müssen:

Eine ist die mittlere Position der Sequenz mid_pos.

• Eins ist der Mittelwert mid_val der Sequenz.

• Jetzt lernen Sie den Algorithmusprozess der binären Suche kennen, indem Sie nach dem Schlüsselwort 8 in der Sequenz nums=[1,3,4,5,8,10,12] suchen.
  Bevor Sie die binäre Suche durchführen, definieren Sie zunächst zwei Positionsvariablen (Zeigervariablen): 🎜🎜🎜🎜Der linke Zeiger l_idx zeigt zunächst auf die Nummer ganz links in der Sequenz. 🎜🎜🎜🎜Der rechte Zeiger r_idx zeigt zunächst auf die Nummer ganz rechts in der Sequenz. 🎜

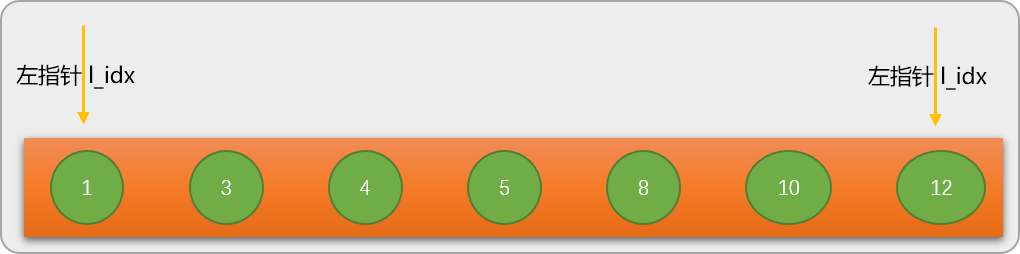
第 1 步：通过左、右指针的当前位置计算出数列的中间位置 mid_pos=3，并根据 mid_pos 的值找出数列中间位置所对应的值 mid_val=nums[mid_pos] 是 5。

二分查找算法的核心就是要找出数列中间位置的值。

第 2 步：把数列中间位置的值和给定的关键字相比较。这里关键字是 8，中间位置的值是 5，显然 8 是大于 5，因为数列是有序的，自然会想到没有必要再与数列中 5 之前的数字比较，而是专心和 5 之后的数字比较。

一次比较后再次查找的数列范围缩小了一半。这也是二分算法的由来。

第 3 步：根据比较结果，调整数列的大小，这里的大小调整不是物理结构上调整，而是逻辑上调整，调整后原数列没有变化。也就是通过修改左指针或右指针的位置，从逻辑上改变数列大小。调整后的数列如下图。

二分查找算法中数列的范围由左指针到右指针的长度决定。

第 4 步：重复上述步骤，至到找到或找不到为止。

编码实现二分查找算法

'''
二分查找算法
'''
def binary_find(nums, key):
    # 初始左指针
    l_idx = 0
    # 初始在指针
    r_ldx = len(nums) - 1
    while l_idx <= r_ldx:
        # 计算出中间位置
        mid_pos = (r_ldx + l_idx) // 2
        # 计算中间位置的值
        mid_val = nums[mid_pos]
        # 与关键字比较
        if mid_val == key:
            # 出口一：比较相等，有此关键字，返回关键字所在位置
            return mid_pos
        elif mid_val > key:
            # 说明查找范围应该缩少在原数的左边
            r_ldx = mid_pos - 1
        else:
            l_idx = mid_pos + 1
    # 出口二：没有查找到给定关键字
    return -1

&#39;&#39;&#39;
测试二分查找
&#39;&#39;&#39;
if __name__ == "__main__":
    nums = [1, 3, 4, 5, 8, 10, 12]
    key = 3
    pos = binary_find(nums, key)
    print(pos)

通过前面对二分算法流程的分析，可知二分查找的子问题和原始问题是同一个逻辑，所以可以使用递归实现：

'''
递归实现二分查找
'''
def binary_find_dg(nums, key, l_idx, r_ldx):
    if l_idx > r_ldx:
        # 出口一：没有查找到给定关键字
        return -1
    # 计算出中间位置
    mid_pos = (r_ldx + l_idx) // 2
    # 计算中间位置的值
    mid_val = nums[mid_pos]
    # 与关键字比较
    if mid_val == key:
        # 出口二：比较相等，有此关键字，返回关键字所在位置
        return mid_pos
    elif mid_val > key:
        # 说明查找范围应该缩少在原数的左边
        r_ldx = mid_pos - 1
    else:
        l_idx = mid_pos + 1
    return binary_find_dg(nums, key, l_idx, r_ldx)
'''
测试二分查找
'''
if __name__ == "__main__":
    nums = [1, 3, 4, 5, 8, 10, 12]
    key = 8
    pos = binary_find_dg(nums, key,0,len(nums)-1)
    print(pos)

二分查找性能分析：

二分查找的过程用树形结构描述会更直观，当搜索完毕后，绘制出来树结构是一棵二叉树。

1.如上述代码执行过程中，先找到数列中的中间数字 5，然后以 5 为根节点构建唯一结点树。

2.5 和关键字 8 比较后，再在以数字 5 为分界线的右边数列中找到中间数字10，树形结构会变成下图所示。

3.10 和关键字 8比较后，再在10 的左边查找。

查找到8 后，意味着二分查找已经找到结果，只需要 3 次就能查找到最终结果。

从二叉树的结构上可以直观得到结论：二分查找关键字的次数由关键字在二叉树结构中的深度决定。

4.上述是查找给定的数字8，为了能查找到数列中的任意一个数字，最终完整的树结构应该如下图所示。

很明显，树结构是标准的二叉树。从树结构上可以看出，无论查找任何数字，最小是 1 次，如查找数字 5，最多也只需要 3 次，比线性查找要快很多。

根据二叉树的特性，结点个数为 n 的树的深度为 h=log2(n+1)，所以二分查找算法的大 O 表示的时间复杂度为 O(logn)，是对数级别的时间度。

当对长度为1000的数列进行二分查找时，所需次数最多只要 10 次，二分查找算法的效率显然是高效的。

然而，二分查找算法在实行之前需要对数列进行排序，因此前面所述的时间复杂度并未包含排序所需的时间。所以，二分查找一般适合数字变化稳定的有序数列。

3. 插值查找

插值查找本质是二分查找，插值查找对二分查找算法中查找中间位置的计算逻辑进行了改进。

原生二分查找算法中计算中间位置的逻辑：中间位置等于左指针位置加上右指针位置然后除以 2。

    # 计算中间位置
    mid_pos = (r_ldx + l_idx) // 2

插值算法计算中间位置逻辑如下所示：

key 为要查找的关键字！！

# 插值算法中计算中间位置
mid_pos = l_idx + (key - nums[l_idx]) // (nums[r_idx] - nums[l_idx]) * (r_idx - l_idx)

编码实现插值查找：

# 插值查找基于二分法，只是mid计算方法不同
def binary_search(nums, key):
    l_idx = 0
    r_idx = len(nums) - 1
    old_mid = -1
    mid_pos = None
    while l_idx < r_idx and nums[0] <= key and nums[r_idx] >= key and old_mid != mid_pos:
        # 中间位置计算
        mid_pos = l_idx + (key - nums[l_idx]) // (nums[r_idx] - nums[l_idx]) * (r_idx - l_idx)
        old_mid = mid_pos
        if nums[mid_pos] == key:
            return "index is {}, target value is {}".format(mid_pos, nums[mid_pos])
            # 此时目标值在中间值右边，更新左边界位置
        elif nums[mid_pos] < key:
            l_idx = mid_pos + 1
        # 此时目标值在中间值左边，更新右边界位置
        elif nums[mid_pos] > key:
            r_idx = mid_pos - 1
    return "Not find"

li =[1, 3, 4, 5, 8, 10, 12]
print(binary_search(li, 6))

插值算法的中间位置计算时，对中间位置的计算有可能多次计算的结果是一样的，此时可以认为查找失败。

插值算法的性能介于线性查找和二分查找之间。

如果序列具有较大数量的均匀分布的数字，插值查找算法的平均执行效率要比二分查找好得多。如果数据在数列中分布不均匀，插值算法并不是最优选择。

4. 分块查找

分块查找类似于数据库中的索引查询，所以分块查找也称为索引查找。其算法的核心还是线性查找。

现有原始数列 nums=[5,1,9,11,23,16,12,18,24,32,29,25]，需要查找关键字11 是否存在。

第 1 步：使用分块查找之前，先要对原始数列按区域分成多个块。至于分成多少块，可根据实际情况自行定义。分块时有一个要求，前一个块中的最大值必须小于后一个块的最小值。

块内部无序，但要保持整个数列按块有序。

分块查找要求原始数列从整体上具有升序或降序趋势，如果数列的分布不具有趋向性，如果仍然想使用分块查找，则需要进行分块有序调整。

第 2 步：根据分块信息，建立索引表。索引表至少应该有 2 个字段，每一块中的最大值数字以及每一块的起始地址。显然索引表中的数字是有序的。

第 3 步：查找给定关键字时，先查找索引表，查询关键字应该在那个块中。如查询关键字 29，可知应该在第三块中，然后根据索引表中所提供的第三块的地址信息，再进入第三块数列，按线性匹配算法查找29 具体位置。

编码实现分块查找：

先编码实现根据分块数量、创建索引表，这里使用二维列表保存储索引表中的信息。

'''
分块：建立索引表
参数：
    nums 原始数列
    blocks 块大小
'''
def create_index_table(nums, blocks):
    # 索引表使用列表保存
    index_table = []
    # 每一块的数量
    n = len(nums) // blocks
    for i in range(0, len(nums), n):
        # 索引表中的每一行记录
        tmp_lst = []
        # 最大值
        tmp_lst.append(max(nums[i:i + n-1]))
        # 起始地址
        tmp_lst.append(i)
        # 终止地址
        tmp_lst.append(i + n - 1)
        # 添加到索引表中
        index_table.append(tmp_lst)
    return index_table
'''
测试分块
'''
nums = [5, 1, 9, 11, 23, 16, 12, 18, 24, 32, 29, 25]
it = create_index_table(nums, 3)
print(it)
'''
输出结果：
[[11, 0, 3], [23, 4, 7], [32, 8, 11]]
'''

代码执行后，输出结果和分析的结果一样。

以上代码仅对整体趋势有序的数列进行分块。如果整体没有向有序趋势发展，则需要提供适当的块排序计划，有兴趣的人可以自行完成。

如上代码仅为说明分块查找算法。

分块查找的完整代码：

'''
分块：建立索引表
参数：
    nums 原始数列
    blocks 块大小
'''
def create_index_table(nums, blocks):
    # 索引表使用列表保存
    index_table = []
    # 每一块的数量
    n = len(nums) // blocks
    for i in range(0, len(nums), n):
        tmp_lst = []
        tmp_lst.append(max(nums[i:i + n - 1]))
        tmp_lst.append(i)
        tmp_lst.append(i + n - 1)
        index_table.append(tmp_lst)
    return index_table

'''
使用线性查找算法在对应的块中查找
'''
def lind_find(nums, start, end):
    for i in range(start, end):
        if key == nums[i]:
            return i
            break
    return -1

'''
测试分块
'''
nums = [5, 1, 9, 11, 23, 16, 12, 18, 24, 32, 29, 25]
key = 16
# 索引表
it = create_index_table(nums, 3)
# 索引表的记录编号
pos = -1
# 在索引表中查询
for n in range(len(it) - 1):
    # 是不是在第一块中
    if key <= it[0][0]:
        pos = 0
    # 其它块中
    if it[n][0] < key <= it[n + 1][0]:
        pos = n + 1
        break
if pos == -1:
    print("{0} 在 {1} 数列中不存在".format(key, nums))
else:
    idx = lind_find(nums, it[pos][1], it[pos][2] + 1)
    if idx != -1:
        print("{0} 在 {1} 数列的 {2} 位置".format(key, nums, idx))
    else:
        print("{0} 在 {1} 数列中不存在".format(key, nums))
&#39;&#39;&#39;
输出结果
16 在 [5, 1, 9, 11, 23, 16, 12, 18, 24, 32, 29, 25] 数列的第 5 位置
&#39;&#39;&#39;

分块查找对于整体趋向有序的数列，其查找性能较好。如果原始数列没有整体有序性，就需要使用块排序算法，其时间复杂度没有二分查找算法好。

建立索引表是分块查找所必需的，但这会增加额外的存储空间，因此其空间复杂度较高。其优于二分的地方在于只需要对原始数列进行部分排序。本质还是以线性查找为主。

Das obige ist der detaillierte Inhalt vonSo implementieren Sie den Python-Suchalgorithmus. Für weitere Informationen folgen Sie bitte anderen verwandten Artikeln auf der PHP chinesischen Website!